こんにちは。kzです。
前回、集合論をまとめました。今回は位相空間論です。この分野は機械学習に密接に関係しているものになります。例えば
- Reproducing Hilbert Space
- Dimension Reduction
位相空間
定義
次の条件を満たすXの部分集合の族UをXの開集合系という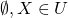
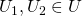 なら、
なら、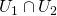
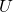 の元からなる任意の集合族
の元からなる任意の集合族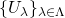 に対し、
に対し、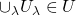
命題
位相空間Xの閉集合全体の集合Fは次の性質を満たす.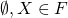
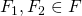 なら、
なら、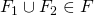
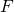 の元からなる任意の集合族
の元からなる任意の集合族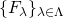 に対し、
に対し、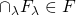
命題
集積点と孤立点
命題
ポイントとしては、位相空間は開集合のある空間ということですね。もっと雑にいうと「近さの概念」だと思ってもらっていいです。(違うんですけどね)位相にも密着位相など色々あるんですけど、これから距離などの議論を進めるための準備だと思ってくれるといいです。
定義
Xを位相空間とする.- 任意の
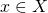 に対して、一点集合
に対して、一点集合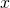 が
が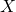 の閉集合になるならば、
の閉集合になるならば、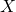 を
を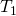 空間という.
空間という. - 任意の
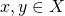 に対して、
に対して、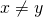 ならば、開集合
ならば、開集合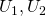 で
で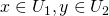 かつ
かつ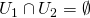 を満たすものが存在するとき、
を満たすものが存在するとき、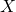 を
を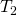 空間またはハウスドルフ空間という.
空間またはハウスドルフ空間という. - 任意の
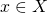 と
と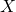 の閉集合
の閉集合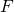 に対して、
に対して、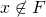 ならば、開集合
ならば、開集合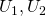 で
で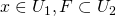 かつ
かつ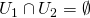 を満たすものが存在するとき、
を満たすものが存在するとき、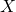 を
を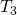 空間という.
空間という.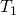 条件を満たす
条件を満たす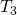 空間を正則空間という.
空間を正則空間という. - 任意のXの閉集合
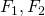 に対して、
に対して、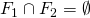 ならば、開集合
ならば、開集合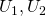 で
で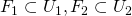 かつ
かつ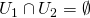 を満たすものが存在するとき、
を満たすものが存在するとき、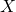 を
を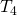 空間という.
空間という.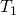 条件を満たす
条件を満たす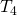 空間を正規空間という.
空間を正規空間という.
命題
ハウスドルフ空間の収束点列の極限点は一意的に定まる.空間が出てきましたが、覚えておくべきは「ハウスドルフ空間」です。次元削減の「T-SNE」において「多様体」というものが出てきますが、そこでハウスドルフ空間が大切になります。また、数学では「一意」が結構大切です。
連続写像
命題
命題
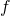 は連続写像である.
は連続写像である. 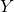 の任意の開集合
の任意の開集合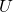 に対して、
に対して、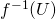 が
が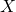 の開集合になる.
の開集合になる.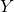 の任意の閉集合
の任意の閉集合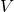 に対して、
に対して、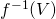 が
が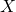 の閉集合になる.
の閉集合になる.
定義
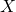 の任意の開集合
の任意の開集合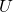 に対して、
に対して、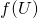 が
が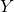 の開集合になるとき、
の開集合になるとき、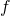 を開写像という.
を開写像という.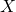 の任意の閉集合
の任意の閉集合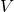 に対して、
に対して、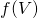 が
が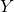 の閉集合になるとき、
の閉集合になるとき、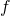 を閉写像という.
を閉写像という.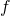 が連続な全単射であり、逆写像
が連続な全単射であり、逆写像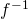 も連続であるとき、
も連続であるとき、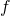 を同相写像という.
を同相写像という.
命題
命題
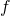 は同相写像である.
は同相写像である.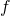 は連続な全単射開写像である.
は連続な全単射開写像である.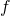 は連続な全単射閉写像である.
は連続な全単射閉写像である.
個人的にな意見ですが、「連続=開集合」のイメージを持っています。特に多様体の証明の時にめっちゃ使うイメージです。
距離空間
定義
次の性質を満たす関数- 任意の
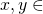 Xに対して、
Xに対して、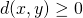 が成り立つ.
が成り立つ. 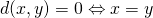
- 任意の
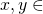 Xに対して、
Xに対して、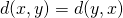 が成り立つ.
が成り立つ. - 任意の
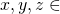 Xに対して、
Xに対して、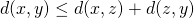 が成り立つ.
が成り立つ.
定理
距離の定義は覚えましょう。KLは距離ではありません。JS divergenceは対称性を加味したものですね。
コンパクト空間
命題
定理
コンパクト空間からハウスドルフ空間への連続な全単射は同相写像である補題
最大値・最小値の定理
定理
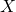 はコンパクトである.
はコンパクトである.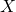 は点列コンパクトである.
は点列コンパクトである.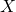 は全有界かつ完備である
は全有界かつ完備である
定理
中間値の定理
とりあえず、コンパクトだと便利なんです。また、私たちが議論する場はほとんどが実数世界なので「コンパクト=有界閉集合」なんです。なのでイメージしやすいと思います。イメージとしては覆得れば良いので水溜りも球体もコンパクトです。今回は位相空間論でした。基礎を部分的にまとめただけなので詳しく知りたい人は数学書を読んでください。T-SNEなどの論文を軽く見るのもいいかもしれません。
Ghidraが人気のようですがマルウェア解析の記事ももっと書きたいですねえ。でわ。