こんにちは。 素人にfish_shellは無理でした。kzです。 リッジが終わりましたね。ついに来ました

ラッソ

最近色々ラッソについて調べていたんですが、微分不可能な関数の最適化ってやっぱ難しいですね。機械学習において非常に重要な２つのキーワード – ラグランジュの未定乗数法 – KKT条件 は別の記事でゆっくり解説します。では本題に入りましょう。

Lasso

過学習を考慮した回帰モデルの一つ – L_1正則化項を使用した回帰model – スパース性を考えるときに用いる（これについては次の記事で詳しく説明します。）

(1)   \begin{align*} \beta = \texttt{argmin}_b { |y-Xb |^2_2 + \lambda|b|_1^1 } \end{align*}

リッジ回帰との唯一の違いは正規化項がL1(絶対値)であるということ。

微分できない？

ちょっと微分について復習しよう。おまけで複素解析も出てくるよ

L1とL2

これまでに何度か説明していると思いますがまずは – 微分可能性 が大きな違いです。L1は尖っているので0で微分できませんね。

他の違いは？

リッジ回帰ではデカイパラメータbがでかくなりすぎないよう上限を設けましたね。 ラッソも上限はありますが、ゼロがKEYWORDです。なぜなら – 無関係な特徴量はゼロで排除する という特徴があります。ゆえに、モデルで初めに設定したものよりも少ない特徴量で済む可能性があります。これが先ほどのスパース性と言われる所以です。

パラメータが0を図から考察

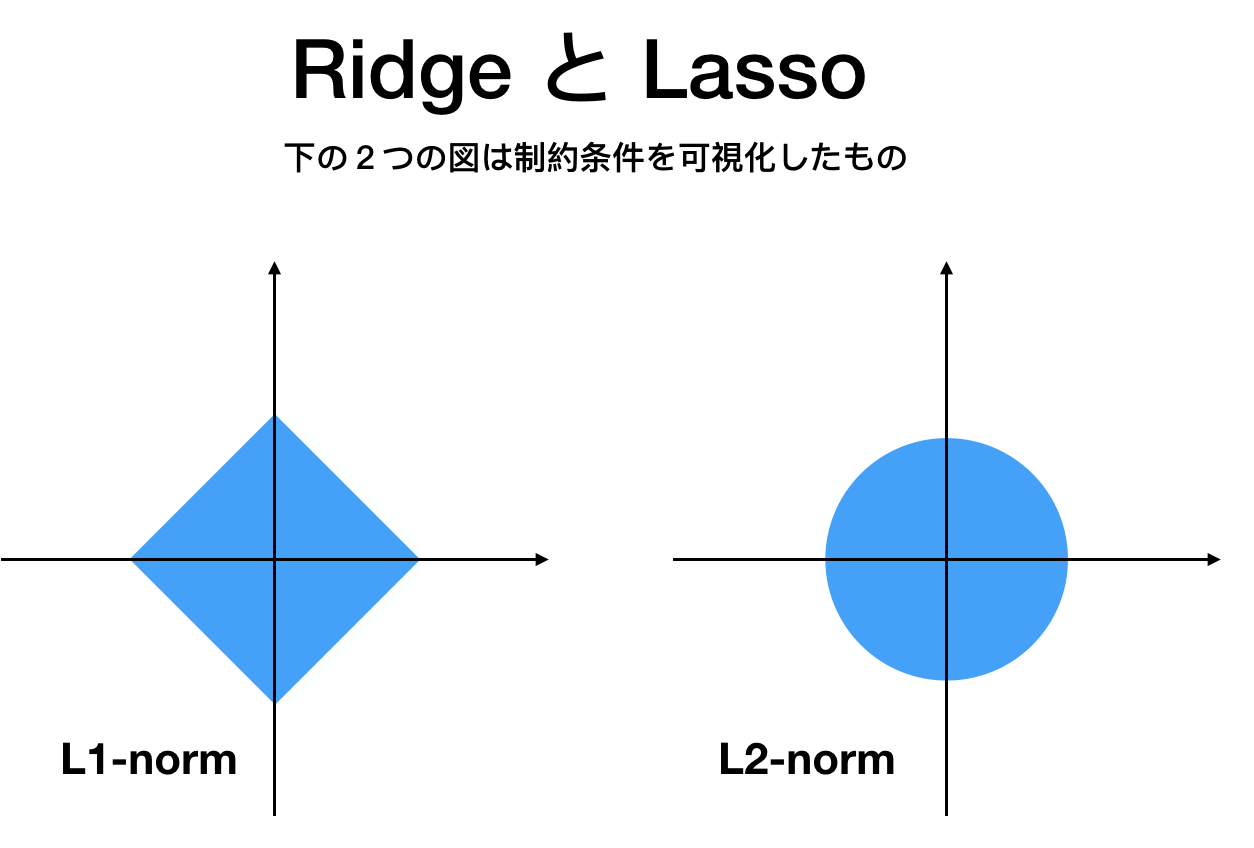
では図を用いて直感的に理解しましょう。次の図はRidge,　Lassoを議論するときに使われるとてもポピュラーなものです。

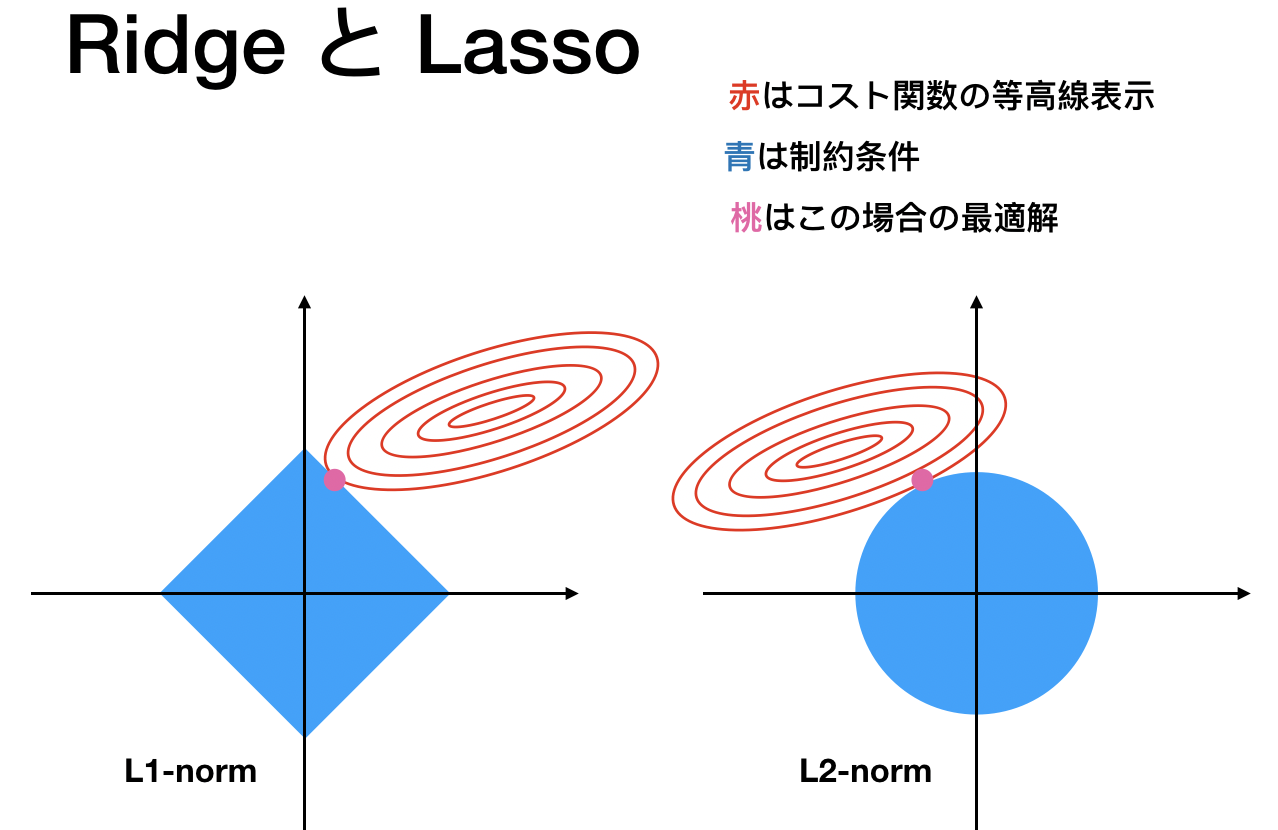
「スパース」とは「スカスカ」なイメージ

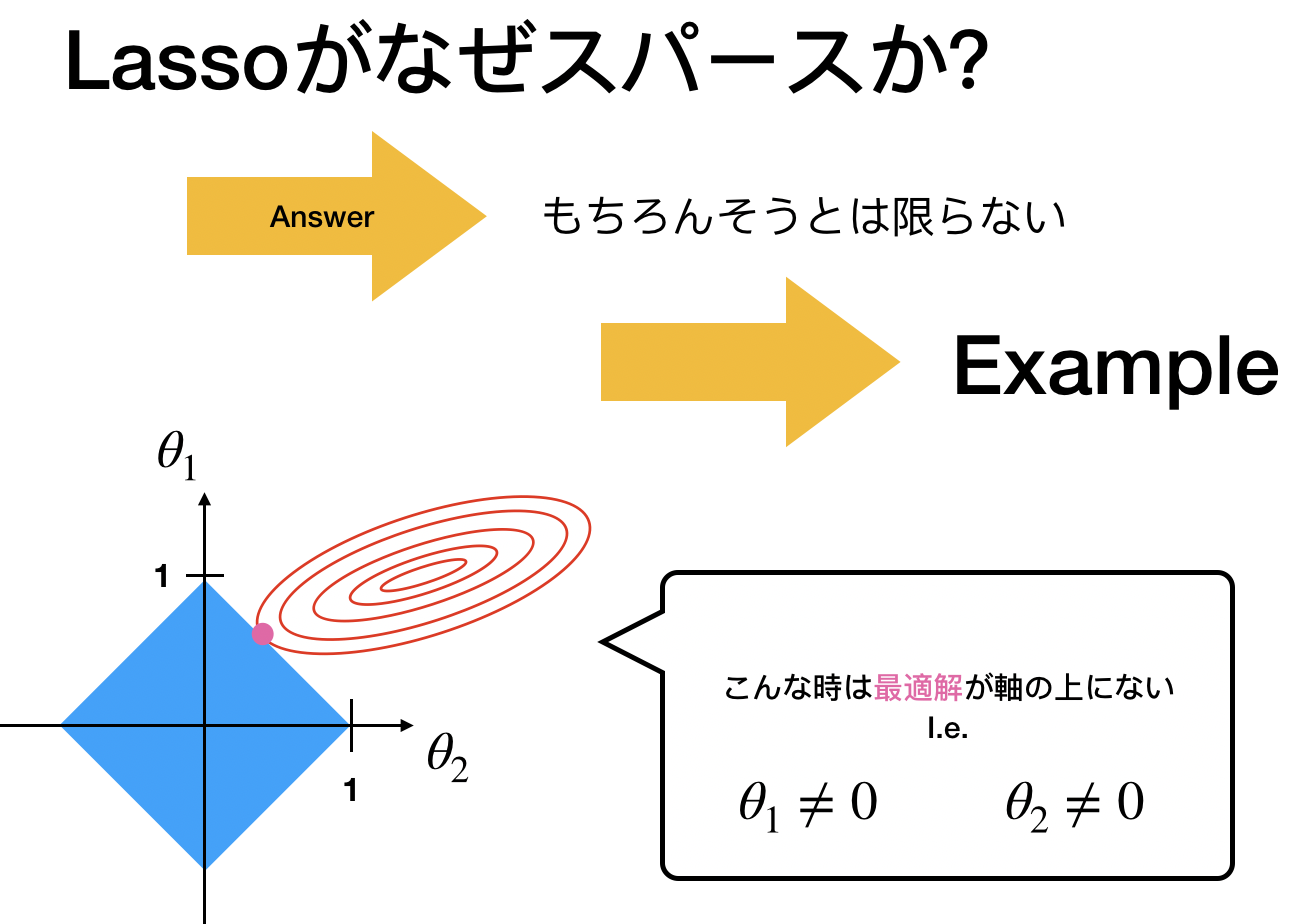
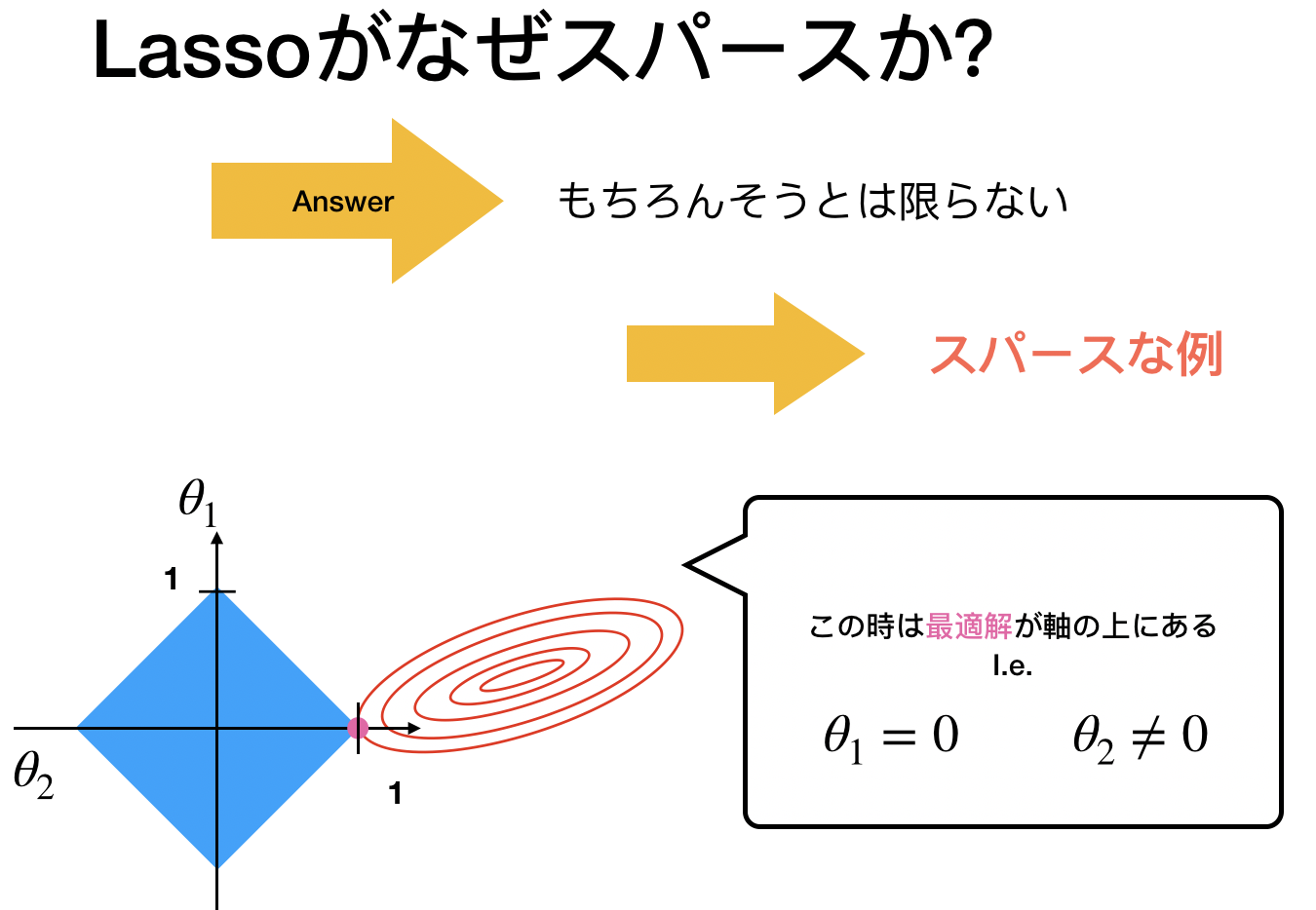
つまり、ゼロがいっぱいあるイメージでいい。 しかし重要なのは常にスパースなわけじゃないこと。 スパースと言われるのはこの「尖ったポイント」に最適解がある時。 これはL1だからできますよね。L2は円だったのでスパース性はありません。

パラメータが0を数式から考察

次のように超シンプルな回帰モデルを考えます。(以下転置使ってますが無くてもいいです)

(2)   \begin{align*} y = bx + \epsilon \end{align*}

次の最小化を考えます。

(3)   \begin{align*} \texttt{minimize } y^Ty - 2y^T xb + b x^Tx b + 2\lambda |b|_1^1 \end{align*}

(この2は計算の都合上のもの)

ここで解がb>0と仮定します。

すると、y = bx \Leftrightarrow <y,y> = b<y,x>より y^Tx >0と仮定するのと同値であることがわかります。さて、目的関数をbに関して微分しましょう

仮定より今は微分できます

(4)   \begin{align*} \frac{\partial }{\partial b} \texttt{objective function} = -2y^Tx + 2x^Tx b + 2\lambda \end{align*}

であり、これをゼロと置くことでこの解は次のものだとわかります

(5)   \begin{align*} b = \frac{y^Tx - \lambda}{x^Tx } \end{align*}

ここで\lambdaを増やしていくと\lambda = y^Txでゼロになることがわかりますね。 この瞬間にLassoはスパース性を持ちます。

一方、リッジの場合は　

(6)   \begin{align*} \textrm{minimize } & y^Ty - 2y^T xb + b x^Tx b + 2\lambda |b|_2^2　 \end{align*}

(7)   \begin{align*} b &= \frac{y^Tx}{x^Tx + \lambda} \end{align*}

となるので、b \neq 0よりパラメータはゼロにはならないですね。 でわ