こんにちは。
初の記事はニュートン法についてです。(理論編)と(実装編)の2回に分けて進めていきます。今回はまずニュートン法を定義から確認し、そのイメージを掴みましょう。ではスタート。
簡単のため先ずは一次元の場合を考える。ある種の関数は方程式の解の形で現れる。
例えば
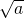
という関数は
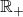
に方程式
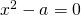
の正の解を対応させる関数です。このような関数の値を求めることは方程式を解くこと、すなはち
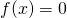
を満たすxを求めることと同値です。その方程式が線形つまり
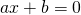
のような形をしているときはその解は容易に求まります(多次元になると連立方程式を扱うことになるのでそういった意味では難しい)。そこで問題になるのが方程式が非線形の場合です。
ニュートン法はそんな非線形な方程式を解くための数値解法の一つです。先ずはその定義を見ましょう。
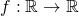
が
- 区間
![Rendered by QuickLaTeX.com [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) で二回微分可能
で二回微分可能
![Rendered by QuickLaTeX.com f'(x)>0, \forall x\in [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-b2a414d17d516a5ebed0a40a95d8673c_l3.png) (単調増加性)
(単調増加性)![Rendered by QuickLaTeX.com f''(x)>0, \forall x\in [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-520d389144b61179dd389d67154e79ad_l3.png) (下に凸)
(下に凸)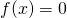 が解を持つ
が解を持つ
を満たし、さらにfおよびf’が計算可能であるとき
”前の数xから
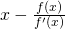
を計算し、それを次のxとする”を繰り返すことにより
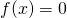
の
![Rendered by QuickLaTeX.com [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png)
の解(単調性の仮定より唯一)が求まる。
なんでこれで解が求まるんだ!と思いますよね、実数の連続性とか中間値の定理とかを使うと証明できるんですけどここではもっと直感的に理解しましょう。
先ず一つ
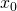
を取ります。関数
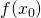
を通る直線は
![Rendered by QuickLaTeX.com \[y = f(x_0) + f'(x_0)(x-x_0)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-c8652f45b05a8efac166f3811a144d2d_l3.png)
と書けます。ではこの直線とx軸との交点、つまり
![Rendered by QuickLaTeX.com \[0 = f(x_0) + f'(x_0)(x-x_0) \]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-eba4b6c66618f974339d265a14ad7c65_l3.png)
を見てみます。式を変形すると
![Rendered by QuickLaTeX.com \[x = x_0 - \frac{f(x_0)}{f'(x_0)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-cb5bdb818fe49b2c11b08ab7bc9bbb41_l3.png)
となります。
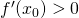
を仮定すると
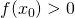
の時、右辺第2項は正なので
![Rendered by QuickLaTeX.com \[x < x_0\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-d481fcd281c4ea0a0650b7da551f10b5_l3.png)
が成り立ちます。(逆も同様)さらに単調増加性より
![Rendered by QuickLaTeX.com \[f(x) < f(x_0)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-158d2d37499cc45cf76db7f4a58f2c11_l3.png)
です。式から分かることは関数の値を減少するように座標の移動しているんですね。これを図で見てみると

となり、確かに求める解(赤色)に近づくように移動していることがわかります。これがニュートン法です。
ニュートン法についての説明を終えて余談に入ります。
機械学習では目的関数の最適化が目標になります。目的関数とはこの場合で言えば
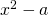
です。そしてこの場合の最適化とは最小化を意味します。(最大化よりも最小化を最適化という方が個人的に多いと思います)そこでどうやって最適化しようか、とみんな悩みます。その手法の一つが今回のニュートン法です。他にも最急降下法、新しいものではAdamなどがあります。どれが一番良い、ということはないので状況に応じて良いものを選びましょう。
また、上の方で直線の式を使いましたが一般的にはテイラー展開を使って話を進めることが多いです。テイラー展開は関数の多項式近似です。条件はありますが、ほとんどの関数はテイラー展開により多項式に変換できます。なので今回の場合だと
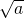
をニュートン法で求めましたがテイラー展開によりもっと簡単に求めることができます。
![Rendered by QuickLaTeX.com \[f(2) = \sqrt{2} = f(1) + \frac{1}{2}(2-1)^1 - \frac{1}{8}(2-1)^1 + \frac{1}{16}(2-1)^1 - \cdots\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-a7ddb2d58c64686dc6ad45c216fd9582_l3.png)
これは
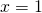
周りのテイラー展開です。機械学習に限らず問題を考えるときに局所的、小さい範囲で考えることは多いと思います。テイラー展開は局所的に関数を見ることができるのでそういう時に便利だと思います。
余談はこれくらいにして次回はニュートン法の簡単な実装とテイラー展開について見てみたいと思います。
指摘&アドバイスお願いします。
引用画像: http://tutorial.math.lamar.edu/Classes/CalcI/NewtonsMethod.aspx
![Rendered by QuickLaTeX.com [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png) で二回微分可能
で二回微分可能![Rendered by QuickLaTeX.com f'(x)>0, \forall x\in [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-b2a414d17d516a5ebed0a40a95d8673c_l3.png) (単調増加性)
(単調増加性)![Rendered by QuickLaTeX.com f''(x)>0, \forall x\in [a,b]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-520d389144b61179dd389d67154e79ad_l3.png) (下に凸)
(下に凸)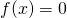 が解を持つ
が解を持つ![]()
![]()
![]()
![]()
![]()
 となり、確かに求める解(赤色)に近づくように移動していることがわかります。これがニュートン法です。
ニュートン法についての説明を終えて余談に入ります。
機械学習では目的関数の最適化が目標になります。目的関数とはこの場合で言えば
となり、確かに求める解(赤色)に近づくように移動していることがわかります。これがニュートン法です。
ニュートン法についての説明を終えて余談に入ります。
機械学習では目的関数の最適化が目標になります。目的関数とはこの場合で言えば![]()
![]()
![]()
![]()
![]()
![]()
 となり、確かに求める解(赤色)に近づくように移動していることがわかります。これがニュートン法です。
ニュートン法についての説明を終えて余談に入ります。
機械学習では目的関数の最適化が目標になります。目的関数とはこの場合で言えば
となり、確かに求める解(赤色)に近づくように移動していることがわかります。これがニュートン法です。
ニュートン法についての説明を終えて余談に入ります。
機械学習では目的関数の最適化が目標になります。目的関数とはこの場合で言えば![]()