こんにちは。
前回レコメンデーションの入門を行いました。
シンプルなMatrix Factorizationで終わってしまったので今回は一つ発展したBiased-Matrix Factorizationを実装してみようと思います。その前に簡単な解説から入りましょう。
Biased-Matrix Factorization
前回のSimple Matrix Factorizationをおさらいすると次のような分解でした。
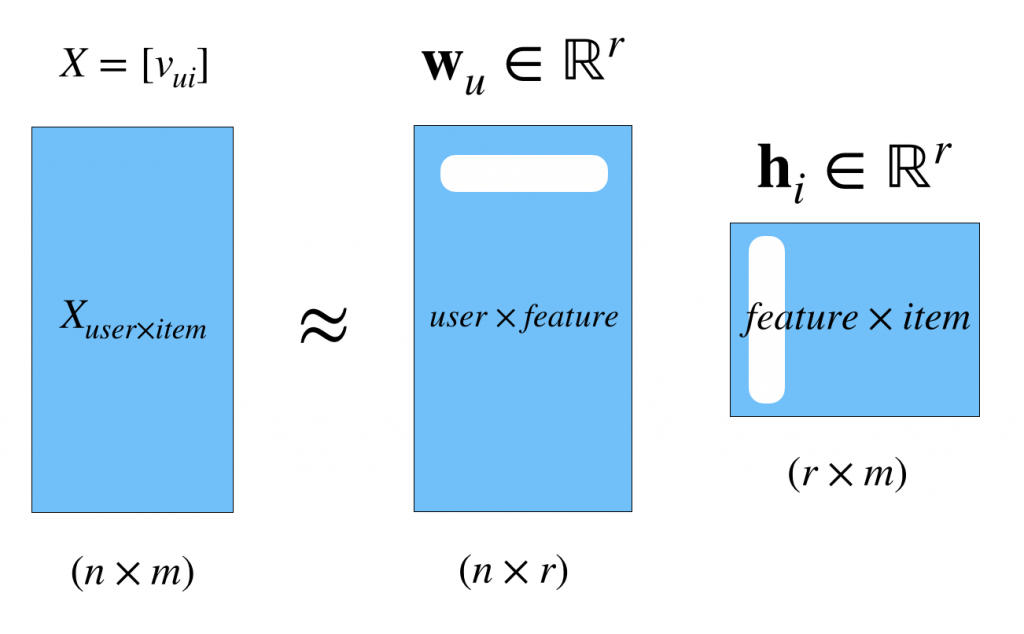
そして、モデルとそのコスト関数は次のように表されるのでした。

しかし、次のような場合を考えてください。Aさんは非常に映画マニアで彼のratingは非常に辛口、つまり平均が低いとしましょう。たとえば1.5にしましょう。一方でBさんは一般的は普通の映画愛好家で平均3.8のratingをするとしましょう。
この時、お互いが同じとある映画「ミイダスリサーチ」を見たとします。Aさんは辛口にもかかわらずratingを4としたとします。そしてBさんは安定に3.8より少し高い4をつけたとします。
ここでデータ![]() には
には![]() と同じ値が入るわけです。しかし、仮定から察することができるようにユーザーごとのバイアスを考えるとこの4を同じ扱いにするのはよくないのではないか?と思うのが普通ですよね。同様の考えでアイテム(今の場合映画)自体にもバイアスを考慮したモデルを考えます。
と同じ値が入るわけです。しかし、仮定から察することができるようにユーザーごとのバイアスを考えるとこの4を同じ扱いにするのはよくないのではないか?と思うのが普通ですよね。同様の考えでアイテム(今の場合映画)自体にもバイアスを考慮したモデルを考えます。
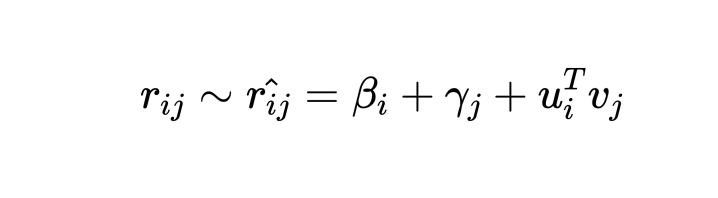
![]() がそれぞれユーザー
がそれぞれユーザー![]() 、アイテム
、アイテム![]() のバイアスになります。そしてこのモデルのコスト関数は前回と似た形になります。
のバイアスになります。そしてこのモデルのコスト関数は前回と似た形になります。
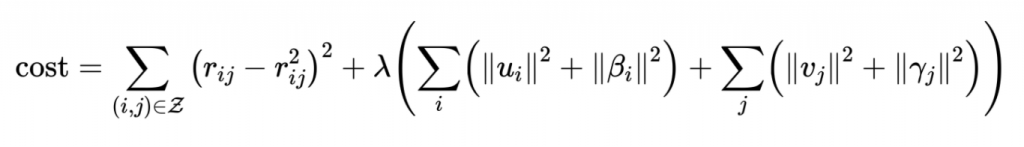
ただ、これでは第二項の中がスマートではないので新たに変数を次のように定義することで前回と全く同じコスト関数をえることができます。
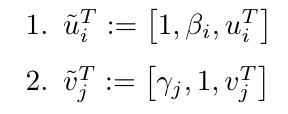
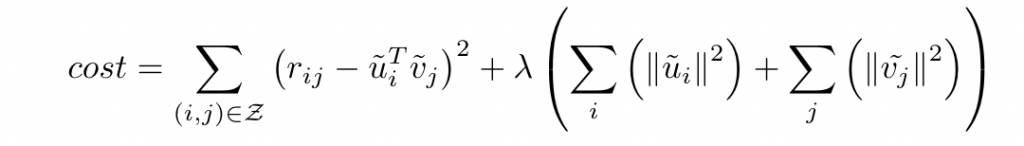
で、思ったんですけどこれってリッジ回帰とめっちゃ似てるんですよね。ということはあの頃のように閉じた解が見つかるはずなんです。
しかし、今回は![]() がベクトルではなく行列なのでその点だけ注意が必要です。そこでこちらの論文が登場します。
がベクトルではなく行列なのでその点だけ注意が必要です。そこでこちらの論文が登場します。

この論文を参考にすると次のようにパラメータ更新のための解がもとまります。
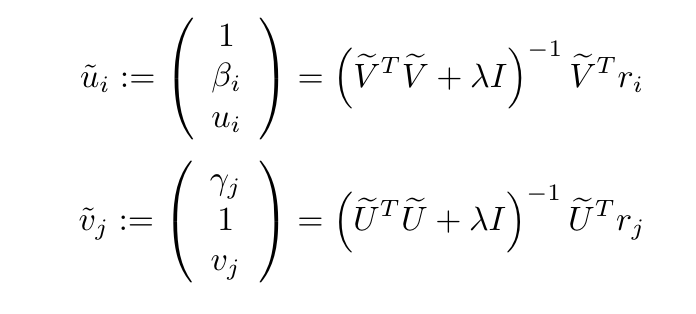
詳しい導出は論文の説明も必要でちょっと長くなるので、纏めだけ貼って簡単に説明します。![]() というフラグを定義します。ユーザー
というフラグを定義します。ユーザー![]() 、アイテム
、アイテム![]() です。そして
です。そして![]() が今回でいうバイアスのようなものです。論文中ではconfidenceという単語になっています。パラメータ
が今回でいうバイアスのようなものです。論文中ではconfidenceという単語になっています。パラメータ![]() でratingに重みづけしたのち、1を加算することで最終的なconfidenceを定義しています。
でratingに重みづけしたのち、1を加算することで最終的なconfidenceを定義しています。
あとはいつも通り微分をとっていくだけです。行列で書き直すときに僕はよく頭がこんがらがるんですがそこは耐えです。

で、今回の更新式をどうやって得たかといいますと![]() としただけです。
としただけです。

結果から言いますとSMFの方がいい結果が得られました。というのは元の行列と予測を引き算してフロベニウスノルムの平方でlossを比較した結果、SMFの方が小さかったからです。ただ、パラメータのチューニングなどは行っておらず、実装にのみ焦点を当てたのでそうなってしまっただけかもしれません。
まだNon-Negative Matrix Factorizationというものがあるらしいです。。。。でわ