ホーム » 機械学習 » SVM実装の際に困った双対とは

SVM実装の際に困った双対とは

投稿者: in 機械学習 投稿日:
こんにちは。

SVMのNumpy実装が非常に難しいです。SMOというアルゴリズムが主流で他には単一法などがあるようですが難しすぎます。そこで僕は下界または上界を最適化、勾配法でやろうと思っているのですがうまくいかずずっと止まっている状態です。

SVMの実装自体非常に少ないと思うのですが理論面について述べている記事はさらにありません。ここでは理論面の「双対」に焦点を置いて解説したいと思います。解説にあたってこのレジュメを使用します。

双対の例題

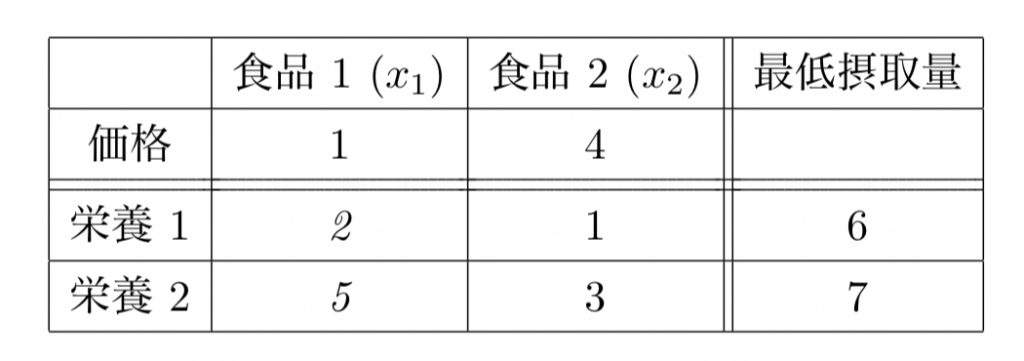
必要な栄養を摂りながら食費を最小にするには どのような割合で二つの食品を購入すれば良いか?

(1)   \begin{align*} (\mathcal{P}) \textrm{ Minimize } x + 4y\ \textrm{Subject to } 2x + y \geq 6 , 5x + 3y \geq 7 , x,y \geq 0 \end{align*}

一方で、必要な栄養を摂りながら食費を最小にするにはどのような割合で二つの食品を購入すれば良いか？
この時、問題(\mathcal{P})より商品1(x)、2(y)に含まれる栄養の価格をそれぞれ見積もると
  • 「栄養1が2単位」　+ 「栄養2が5単位」　= 「価格 1」
  • 「栄養1が1単位」　+ 「栄養2が3単位」　= 「価格 4」
となる。ここで栄養素1を含むものをビタミン剤1としその単位あたりの値段をaとする、同様にもう一方をbとすると

(2)   \begin{align*} 2a + 5b \leq 1 , a + 3b \leq 4 \end{align*}

となるようにビタミン剤の価格を設定すればよいです。また、最低摂取量よりビタミン剤1は6単位、ビタミン剤2は7単位、それぞれ購入されます。したがって、食品との競合に負けずに利益を最大にするように価格を設定するためには次の問題を解けば良いです。

(3)   \begin{align*} (\mathcal{D}) \textrm{ Maximize } 6a + 7b \ \textrm{Subject to } 2a + 5b \leq 1 , a + 3b \leq 4 , a,b \geq 0 \end{align*}

ここからが大切です。ここで各制約が満たされていると仮定し、それぞれの目的関数を比較して見ると

    \[x+4y \geq (2a + 5b)x + (a + 3b)y\]


    \[= (2x + y)a + (5x + 3y)b\]


    \[\geq 6a + 7b\]

となり 「(\mathcal{P})の食品購入費」\geq 「(\mathcal{D})のビタミン剤購入費」 が成り立っていることがわかります。これをコツコツとくと最適解は \mathcal{P} の最小費用 = 3 \geq 3 = \mathcal{D} の最大利益

    \[(a,b) = (\frac{1}{2}, 0) , (x,y) = (3,0)\]

なんと互いに異なる最適化問題の解が一致。ここで初めの問(\mathcal{P})を主問題、続く問題(\mathcal{D})をその双対問題といいます。
ちゃんと進めましたがこれでは僕は全く理解できなかったのでもう少し調べてみました。すると次のことがわかりました。

ラグランジュ緩和

とある問題を解くのが困難な場合、これをもう少し簡単な問題に緩和しようというアプローチしたいですよね。 例えば、問題の制約式をどれか取り除いてしまった問題は、制約が「緩和されている」ことから緩和問題と呼ばれます。しかしながら、制約を取り去ってしまうことは、緩和の度合が激し過ぎて、緩和問題の最適解が元の問題からかけ離れてしまうことがしばしばあります。では制約を取り去ってしまうより、もう少しましな緩和法はないだろうか？ そこで良く使われるのがラグランジュ緩和です。

軸として考える問題を「主問題」と呼びます。双対問題とはその補集合を解くイメージです。今回の例だとMinimize問題をMaximize問題へと変形します。

(4)   \begin{align*} (\mathcal{P}) \textrm{ Minimize } x + 4y\ \textrm{Subject to } 2x + y \geq 6 , 5x + 3y \geq 7 , x,y \geq 0 \end{align*}

さて、これをラグランジュ緩和していきこれに対する双対問題(\mathcal{D})を導出したいと思います。方法としては上で述べたラジグランジュ緩和を用います。

(5)   \begin{align*} (\mathcal{P}) \textrm{ Minimize } x + 4y\ \textrm{Subject to } 2x + y \geq 6 \ 5x + 3y \geq 7 , x,y \geq 0 \end{align*}

これは(\mathcal{P})以下であることが制約よりわかります。もう少し式変形します

(6)   \begin{align*} \textrm{ Minimize }　x + 4y + a(6-(2x + y)) + b(7-(5x + 3y))　　　\ \textrm{Subject to } x,y \geq 0 , a,b \geq 0 \end{align*}

これは主問題の下界です。そこで下界を最大化させることを考えます。そこで注意したいのが以下の二つの制約

(7)   \begin{align*} 1-2a-5b \geq 0 , \ 4-a-3b \geq 0 \end{align*}

これらの意味を考えよう。逆にこれらが成り立たないとすれば

(8)   \begin{align*} 1-2a-5b < 0 , 4-a-3b < 0 \end{align*}

(9)   \begin{align*} 2a + 5b > 1 , a + 3b >　 4 \end{align*}

が導かれます。ここで、この制約下で先ほどの最適化問題

(10)   \begin{align*} \textrm{ Maximize }　6a + 7b \end{align*}

を考えるとどうなります？、そう、これは有界ではなくなり最適解は存在しないことになります。よってこれを考慮すると最終的にラグランジュ緩和によって次の最適化問題に帰着し

(11)   \begin{align*} \textrm{Maximize } 6a + 7b\ \textrm{Subject to } 2a + 5b \leq 1 , \ a + 3b \leq　 4 ,\ a,b \geq 0 \end{align*}

これはまさに先ほどの双対問題\mathcal{D}に他ならないですね。 簡単な例を一つしか用いていないですが主問題から双対問題を導出することができました。最後に簡単にまとめます
  • 「主問題・双対問題」は表裏一体。
  • 双対問題とはラグランジュ緩和を使って下界/上界を最適化する問題
  • 双対問題の制約は有界性を考慮することで生じる
  • 主問題より双対問題の方が簡単に解くことができる時もある

SVMの双対問題

ここまで双対問題とその導出について解説しました。最後に一気に飛んだ議論になりますがせっかくなのでSVMの双対問題を紹介します。

    \[\textrm{Minimize } \frac{1}{2}|w|^2\]


    \[\textrm{Subject to } y_i(w^T x_i + b) \geq 1 \textrm{ for all } 1 \leq i \leq n\]

に対して

    \[\max_\alpha W(\alpha) = \sum_{i=1}^{n} \alpha_i -\frac{1}{2}\sum_{i,j=1}^{n} y_i y_j \alpha_i \alpha_j\]


    \[s.t. \alpha_i \geq 0 , \textrm{ for } i=1,\cdots,n\]


    \[\sum_{i=1}^{n} \alpha_i y_i = 0\]

です。ラグランジュ計算すると出てきます！（なかなか計算がえぐい）SVMは難しいですね、しかし、これをマスターすればかなりレベルアップできると思います。でわ

タグ:

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です