前回、モデルを選択する基準のところで情報量基準という言葉をちょこっと出して、そのままスルーしました。しかし、データ分析においては重要なのでとりあえずその基礎くらいは知っておきましょう。ちなみにコードを書く際にパラメータ選択させられることもあります。
ではそもそも情報量基準とはなんなのか?

では、ここで出る問題は
errorが小さければいいのか? ということです。以前触れましたが、モデルは学習の際に、underfittingやoverfittingを引き起こします。これはパラメータ数によって起こることが多いです。これは明らかですよね。例えば、多項式回帰の字数を増やしまくるとそのモデルはグニャグニャに曲がってデータにフィットしようとしますよね。もちろんfitするということは例えば誤差二乗和を計算すると必ず字数の増加に伴いそれは減少します。しかしこれは、上述の通りoverfittingではないのか?という問題です。
では、問題をまとめると
- 誤差(error)を減らしたい
- 過学習は避けたい
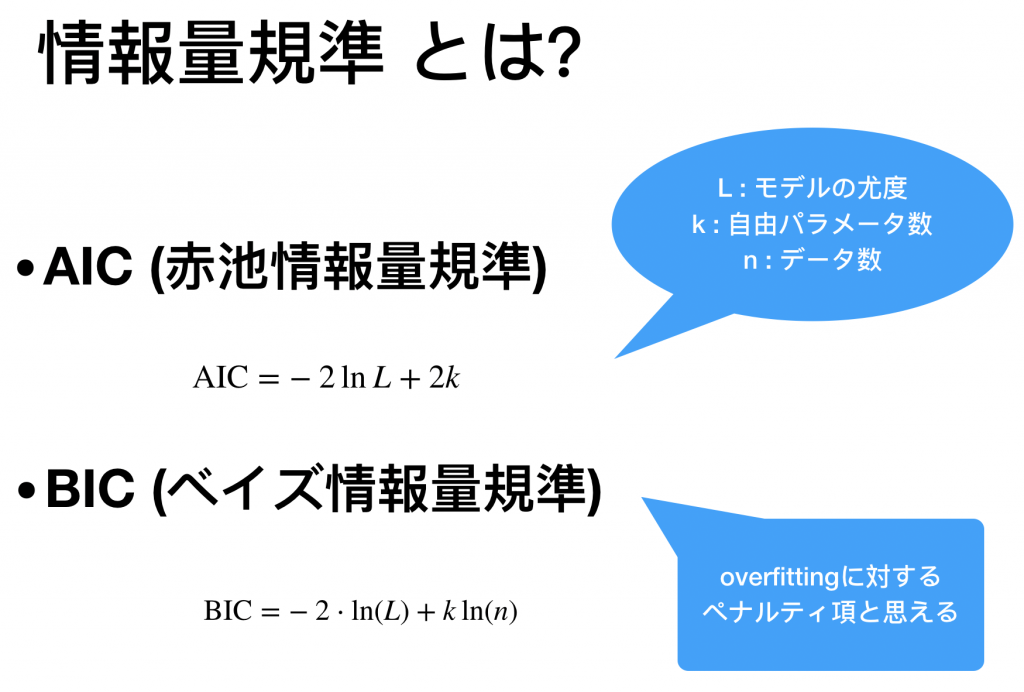
2種類あるねんから使い分けは?ってなりますよね。これについては非常に難しい議論のようです。 上のリンクによると結論としては
- AICとBICを両方使う
- セットで値が小さいモデルを選ぶ
AIC tries to select the model that most adequately describes an unknown, high dimensional reality. This means that reality is never in the set of candidate models that are being considered. On the contrary, BIC tries to find the TRUE model among the set of candidates.ここで重要な点は
- AICはモデルが真である仮定をしてない
- BICは真のモデルがあると仮定して計算してる
![]()
![]()
もう少し、深入りしてみます。
上で、導出の背景と言いましたが次の論文を見てみると AICはKLの最小化を目的として導出されました。一方でBICは事後分布の最大化を目的として導出されました。とはいえ、やはりどちらがいいかはわからないですね、、どっちか選べって言われると僕ならAICですかね。ちなみにKLを知らない人のためにちょこっとだけ説明すると
![]()
![]()
こんな感じで計算します。2つの正規分布間のKLの計算とかやってみるといい練習になると思います。ここで重要なのが1つ。先ほどKLを距離と言いましたが、
KLは距離じゃない
数学をやってる人なら次の例でわかってくれると思います。上の計算は ![]()
KLについて話始めるととんでもなく長くなるのでまた別の記事にして最後にコードを簡単に眺めて終わりましょう。