こんにちは。
正則化パート2ですね。前回の最後に
- Ridge Regression (Tikhonov regularization)
- Lasso Regression
を例に出しました。今回はこれらを用いて正則化について学びましょう。の前に線形回帰を思い出しましょう。その時に
![]()
を考えて
![]()
![]() の列ベクトルが張る空間への射影行列をやりましたね。ここで
の列ベクトルが張る空間への射影行列をやりましたね。ここで![]() が正則ということなのでもう一歩踏み込みQR分解を行います。つまり
が正則ということなのでもう一歩踏み込みQR分解を行います。つまり
![]()
を使うと
![]()
とできます。わかったことは
![]() の列ベクトルが張る空間への射影行列
の列ベクトルが張る空間への射影行列![]() が
が![]() となるということ。超シンプル。これが線形回帰。で、これに
となるということ。超シンプル。これが線形回帰。で、これに![]() 正則化項を加えます。つまり
正則化項を加えます。つまり![]() に対して
に対して
![]()
を考えます。これをリッジ回帰というのでしたね。ラッソは![]() 正則化項を使います。
正則化項を使います。
違いは?
正則化項のノルムです。![]() と
と![]() の違いは?もう少し親しみある言い方だと距離と絶対値の違いは?
の違いは?もう少し親しみある言い方だと距離と絶対値の違いは?
Answer: 微分可能性
![]() は微分できませんね。前回の図を思い出してください。
は微分できませんね。前回の図を思い出してください。![]() は尖っていました。
は尖っていました。
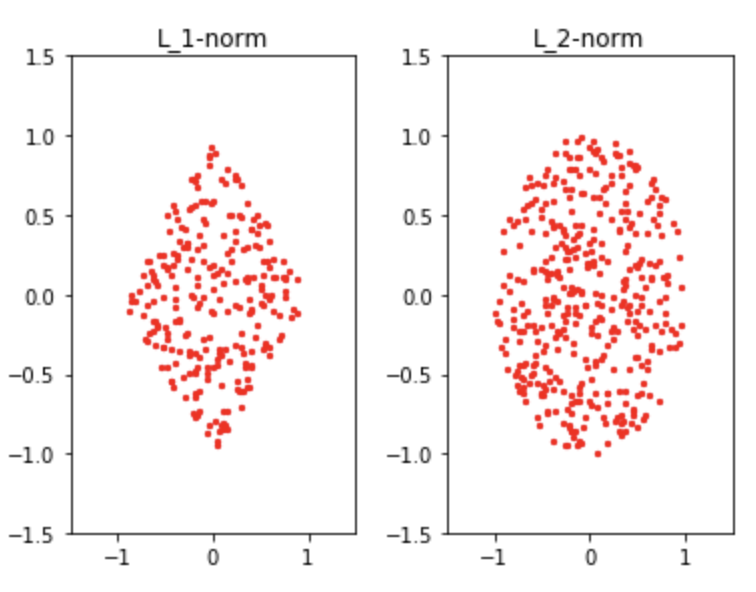
勾配法は微分を使いましたね。なので一旦ラッソは無視してリッジについて学びましょう。
次の解を考えます。ただし![]()
![]()
「アーグミン![]() 」は右辺を最小化するときの
」は右辺を最小化するときの![]() ということ。これを展開し、微分すると
ということ。これを展開し、微分すると
![]()
![]()
![]()
![]()
![]()
これが欲しかった![]() ですね。さっきの
ですね。さっきの![]() と似てませんか?邪魔なのは
と似てませんか?邪魔なのは![]() の項。なのでここで
の項。なのでここで![]() とするとさっきのと同じになります。だって元々のコスト関数の正則化項が0になるわけですからね。
とするとさっきのと同じになります。だって元々のコスト関数の正則化項が0になるわけですからね。
![]() 、これ意味ある?
、これ意味ある?
ここで![]() は半正定値対称行列であり、実数値からなる対称行列は実数の固有値を持ちます。よって
は半正定値対称行列であり、実数値からなる対称行列は実数の固有値を持ちます。よって![]() の固有値は0以上。行列式を計算して見よう。
の固有値は0以上。行列式を計算して見よう。
![]()
![]()
これを![]() について解くと
について解くと![]() の固有値が求まりますね。そこでその固有値の一つを
の固有値が求まりますね。そこでその固有値の一つを![]() とするとリッジ回帰における固有値は
とするとリッジ回帰における固有値は![]() となり、
となり、![]() 分シフトされていますね。つまり、行列式をゼロから遠ざけており正則をキープしてくれています。
分シフトされていますね。つまり、行列式をゼロから遠ざけており正則をキープしてくれています。
逆に![]() とすると
とすると![]() となってしまいますね。これもまずい。
となってしまいますね。これもまずい。
![]() をどうやって決めるか
をどうやって決めるか
これが問題ですね。これは交差検証で選ばれます。交差検証ってなんやあ??
K-fold cross validation
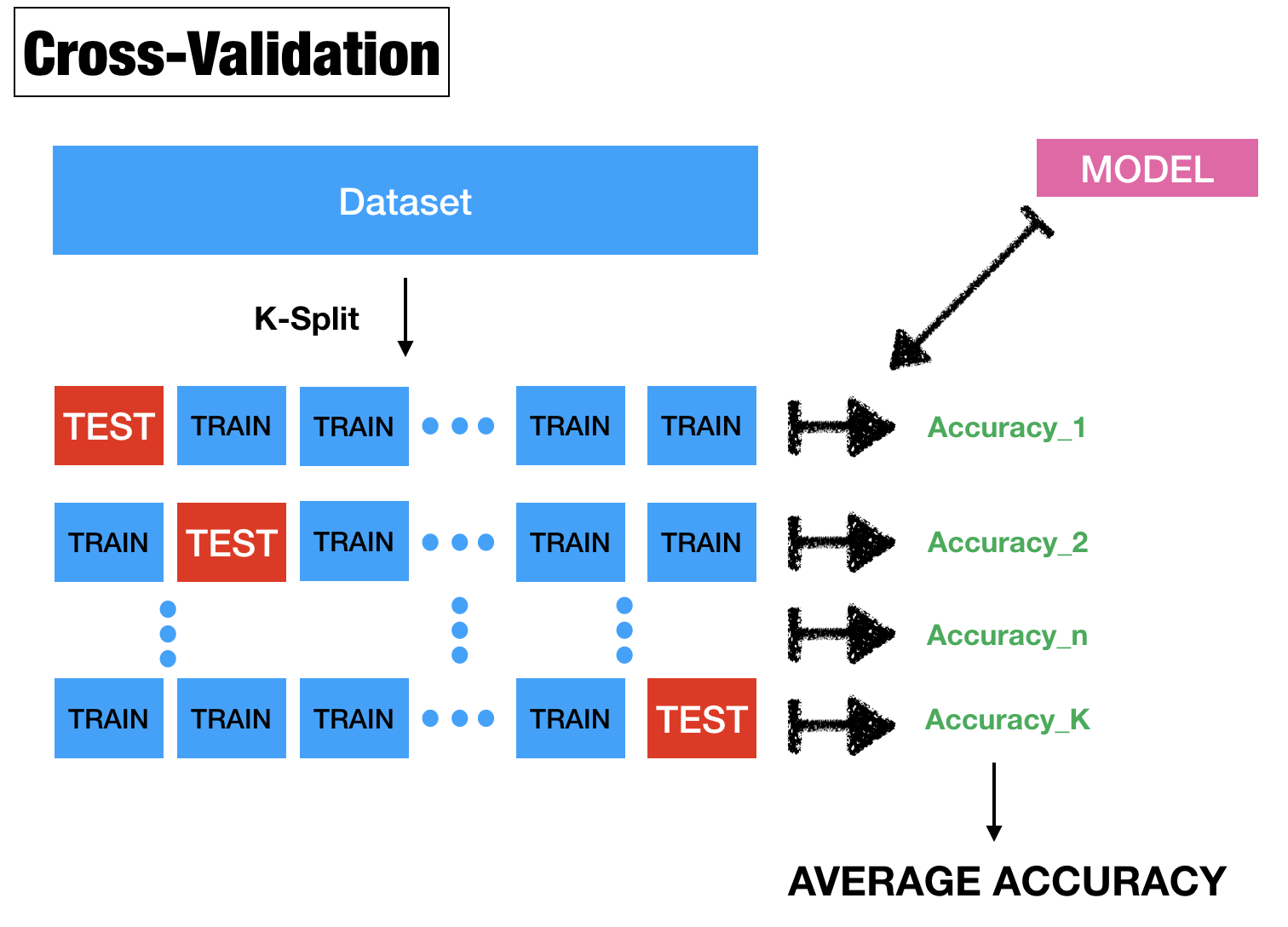
ですかね。これはデータ![]() 個をK等分割(5か10が一般)してモデルの汎化性能を評価するためにあります。しかしここではパラメータ
個をK等分割(5か10が一般)してモデルの汎化性能を評価するためにあります。しかしここではパラメータ![]() のベストチョイスのために使います。これはとても重要な概念なので次の記事で深く確認しましょう。今回は簡単な図を最後に見てお別れです。
のベストチョイスのために使います。これはとても重要な概念なので次の記事で深く確認しましょう。今回は簡単な図を最後に見てお別れです。
でわ
READMORE