線形回帰って何？

2018.11.12

機械学習

こんにちは、本日はとりあえず実装をする前に、パパッとデータの確認です。

$y = 3x - 4 + noise$

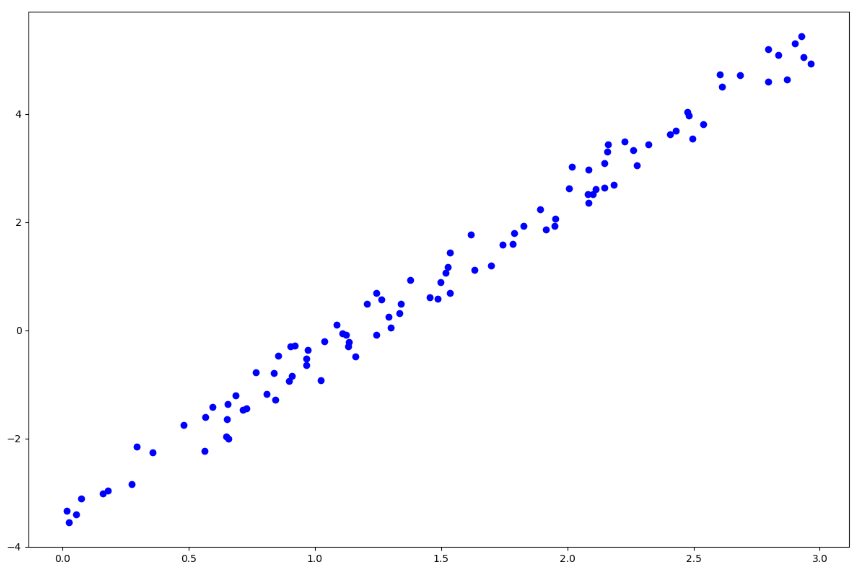
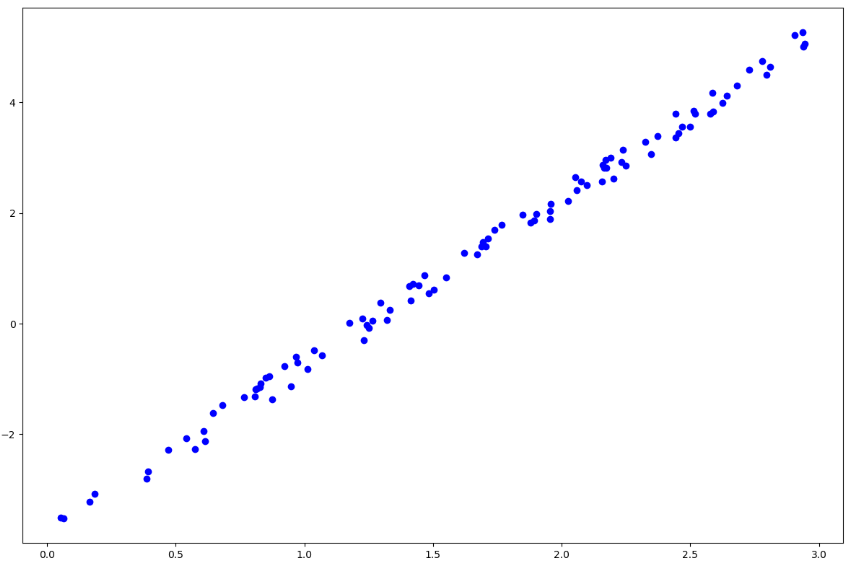
で二つ作りました。見ての通り上の方がノイズが大きいです。今回の予測モデルは直線

$y=mx+b$

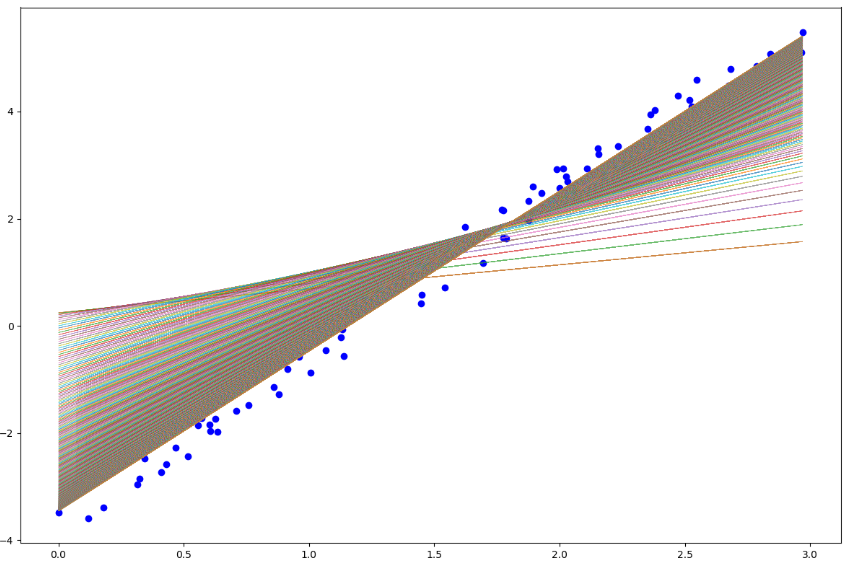
とします。サクッとPYTHONで書くと下のような結果がとれます。まずノイズが小さい方のデータに対して

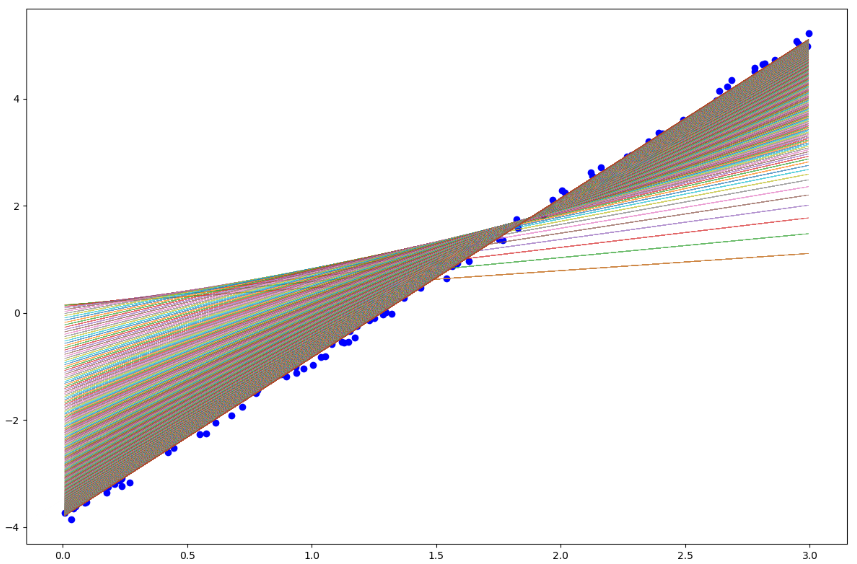
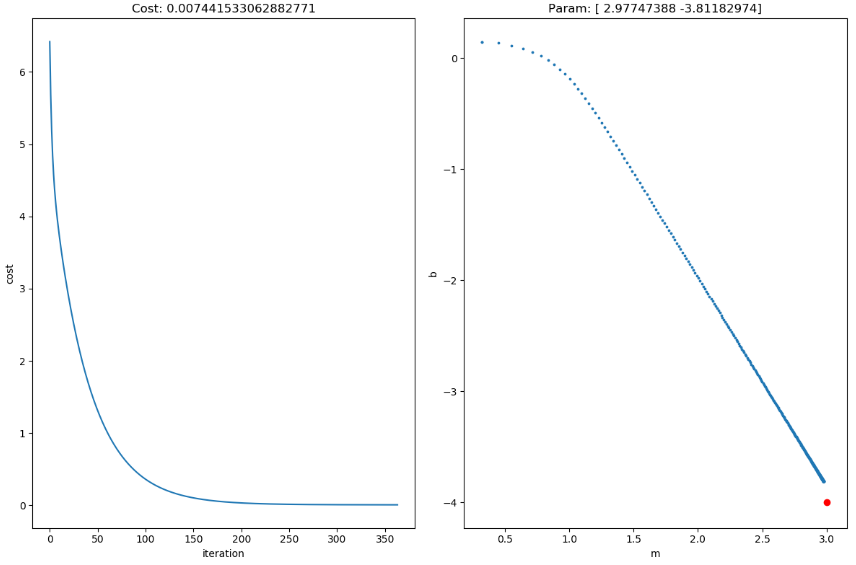
コストが減っており、それに合わせてパラメータ $(m,b)$ も本来の $(3,-4)$ に収束しようとしています。上のプロットが見にくいのですが、学習の際のパラメータ履歴で直線をプロットしたものです。次にノイズが大きい方の結果を見てみましょう。

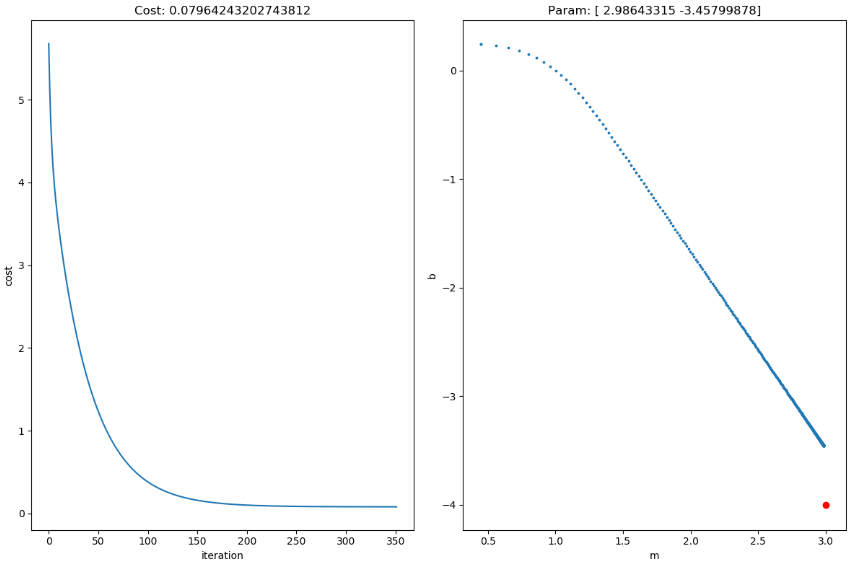
同様にコストも減り、パラメータも本来の値に近ずいてはいますがどおも届きそうにないです。iteration=150あたりで学習が止まっているのでこれ以上は赤点に近づかないでしょう。これはノイズが大きいことが原因です。とりあえず線形回帰を二変数で行いましたが多変数になってもやり方は全く変わりません。コードを書くのが面倒になりますが　sklearnにはすでにlinear regression含め他にも多くの手法があるので簡単に回帰ができます。詳しくは「python 線形回帰 sklearn」などでググればいっぱい出てくるので見てください。

ところで

線形回帰をいい例題にして行列の勉強を簡単にしましょう。というのは何かというと、実は、勾配法使わなくても一発で解が出るんです。

$y_i = 1 * \beta_0 + x_{i1} * \beta_1 + x_{i2} * \beta_2 + \cdots + x_{ik} * \beta_k + \epsilon_i$

というモデルを考えます。これを行列表記すると

$\begin{bmatrix} y_1 \ y_2 \ \vdots \ y_n \ \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1k} \ 1 & x_{21} & x_{22} & \cdots & x_{2k} \ \vdots & \vdots & \vdots & \vdots & \vdots \ 1 & x_{n1} & x_{n2} & \cdots & x_{nk} \ \end{bmatrix} \begin{bmatrix} \beta_0 \ \beta_2 \ \vdots \ \beta_k \ \end{bmatrix} + \begin{bmatrix} \epsilon_1 \ \epsilon_2 \ \vdots \ \epsilon_n \ \end{bmatrix}$

$y = X \beta + \epsilon$

ただし、 $n$ はデータ数、 $k$ は次元（変数の数）とした。ここで前回の理論編を思い出すと今回の最適化は誤差二乗和の最小化であった。よってノルムの定義を思い出せば

$\frac{1}{2} | \epsilon |^2 = \frac{1}{2} | y - X \beta |^2$

を最小化すればいい(1/2は計算上の都合、別になくても良い)、これを計算する。ベクトルの微分については

ここあたりがいい教材だと思う。もちろん「ベクトル　微分」で検索しても多く出てくる。今回使うのは次の3つ。

$\frac{\partial }{\partial x} a^Tx = a$

$\frac{\partial }{\partial x} x^Ta = a$

$\frac{\partial }{\partial x} x^TAx = (A + A^T)x$

では計算すると

$\frac{1}{2} | y - X \beta |^2 = \frac{1}{2} (y - X \beta)^T (y - X \beta)$

$\frac{1}{2} | y - X \beta |^2 = \frac{1}{2} ( \beta^TX^TX \beta - 2y^TX\beta +y^Ty )$

$\nabla_\beta \frac{1}{2} | y - X \beta |^2 = (X^T X + (X^T X)^T)\beta - 2X^Ty$

これを0と置くと

$X^T X \beta = X^Ty$

ここで

$X^T X$ が正則行列を仮定すると

(機械学習の観点から「正則行列」を説明すると「どの列もほとんど似通ってない」になる)

$\beta = (X^T X)^{-1} X^Ty$

と求まる。これが最も誤差が最小であるときのパラメータである。

なんの射影？どこへの射影？

そう、この疑問は大切だ。今私たちが扱っているのは $\frac{1}{2} | y - X \beta |^2$ である。 $X \beta$ についてじーっと見るとこれは $X$ の各列ベクトルの線型結合(四則演算)となることがわかる。たとえば $X = [X_1 X_2 \cdots X_n]$ と表し、 $\beta=[ \beta_1 \beta_2 \cdots \beta_n ]^T$ とすると

$X \beta = X_1 \beta_1 + X_2 \beta_2 + \cdots X_n \beta_n +$