こんにちは。
本日は変分ベイズやります。ちなみに呼び方はいくつかありまして、変文ベイズ、変分推論、Variational Approximation(変分近似)など。
変分とは?
そもそも変分ってなに!って感じですよね。実はこれ微分方程式とか汎関数とかが関わってます。
例えば点推定である最尤法はスコア関数(対数尤度)を微分して解を求めますよね。変分法はこれを拡張した概念です。
つまり、関数の関数の微分が変分です。
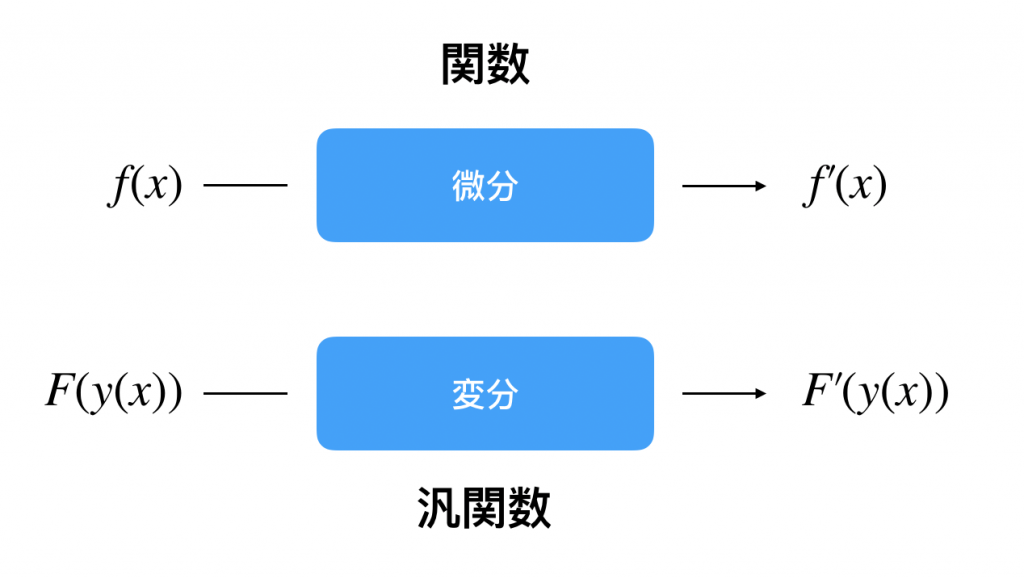
変分とは汎関数の微分です。詳しくは調べていただくとすぐわかりますが例えば最短曲線など求めるときはオイラーラグランジュ方程式と変分法を用いたりします。
変分ベイズとは?
事後分布![]() を求める手法の一つです。MCMCと同じ感じ?と思った方もおられると思います。はい、MCMCも事後分布を求める手法です。
を求める手法の一つです。MCMCと同じ感じ?と思った方もおられると思います。はい、MCMCも事後分布を求める手法です。
ではもういきなりですがVBとMCMCどっちがいいの?という疑問が生まれます。

ずばり、一番の違いは速度です。一般的にはVBの方が早く、計算の多いMCMCは遅いです。データ![]() が多いときはVBの方がいいかもしれません。ただ上にあるようにVBは漸近的に分布を保証するわけではありません。
が多いときはVBの方がいいかもしれません。ただ上にあるようにVBは漸近的に分布を保証するわけではありません。
まずは変分下限の登場です。EMアルゴリズムの時と似てます。
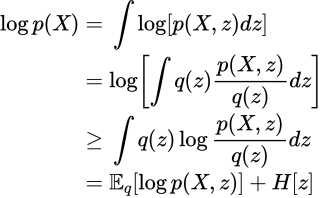
![]() は潜在変数(パラメータ)です。
は潜在変数(パラメータ)です。![]() は前回登場したShannon entropyですね。最後の式が変分下限です、
は前回登場したShannon entropyですね。最後の式が変分下限です、![]() と置くことにします。
と置くことにします。
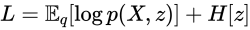
せっかくなのでKLダイバージェンスとの関係も見てみます。
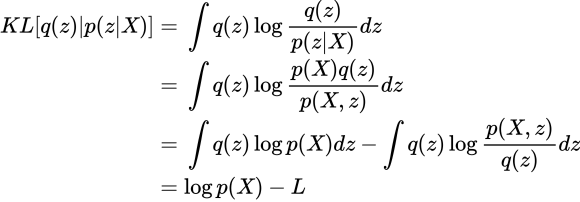
目的は事後分布![]() を近似することです。なので
を近似することです。なので![]() でKL最小化を目指します。式の最後で出てきた
でKL最小化を目指します。式の最後で出てきた![]() は先程と同じ。つまり、KLの最小化は変分下限の最大化に等しいことがわかりました。
は先程と同じ。つまり、KLの最小化は変分下限の最大化に等しいことがわかりました。
しかもよくみてください、KLって汎関数ですよね。
Mean-Field Approximation
変分ベイズでは平均場近似という重要なポイントがあります。これは![]() に与える次の仮定です。
に与える次の仮定です。
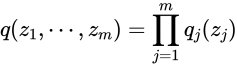
つまり、各潜在変数が独立であると仮定します。すると変分下限は次のように書き直せます。
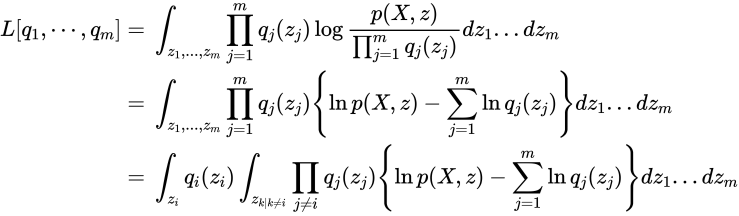
計算を整理するために次を用います。対象の変数以外での期待値です。
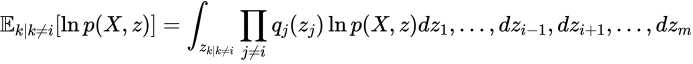
これを用いて先程の式をさらに展開していきます。
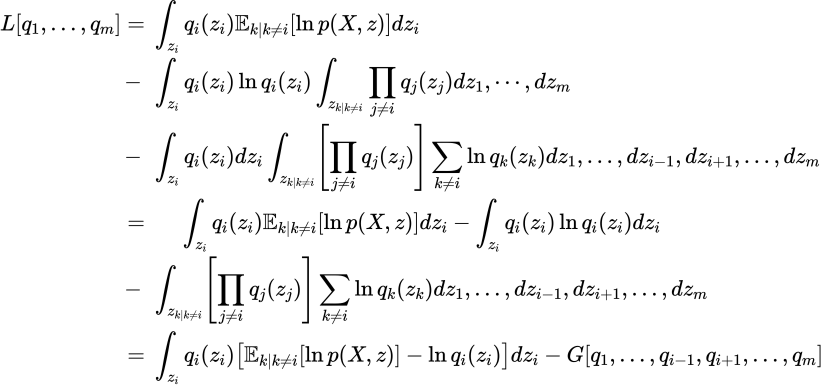
![]() に注目していただければわかりますが、くくりあげています。第二項は
に注目していただければわかりますが、くくりあげています。第二項は![]() を除く
を除く![]() の項です。ラグランジュを用いて次の目的関数を得ます。
の項です。ラグランジュを用いて次の目的関数を得ます。
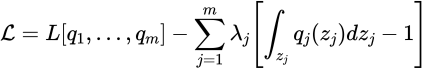
ここで変分法を使います。具体的には![]() に関してEuler-Lagrangeを用います。
に関してEuler-Lagrangeを用います。
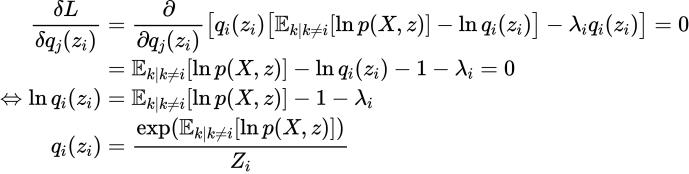
ここで、![]() は正規化定数と呼ばれるものです。以上からわかるように
は正規化定数と呼ばれるものです。以上からわかるように![]() の最適化には他のすべての
の最適化には他のすべての![]() が必要になるのでイテラティブな更新になります。
が必要になるのでイテラティブな更新になります。
一変数ガウスの例
次のような例を考えます。
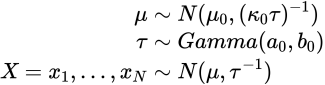
変分ベイズを用いてパラメーラ![]() の分布を逐次的に求めます。まず以下の尤度をばらしておきます。
の分布を逐次的に求めます。まず以下の尤度をばらしておきます。
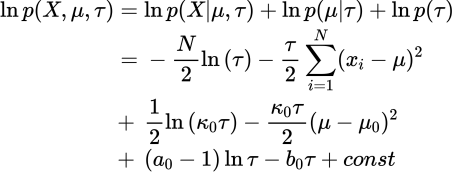
また平均場近似より次を仮定します。
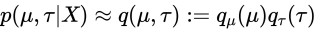
では先程の計算を用いて![]() を計算します。
を計算します。
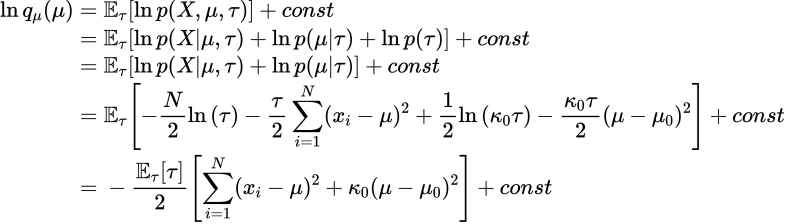
![]() に関して平方完成して以下を得ます。
に関して平方完成して以下を得ます。
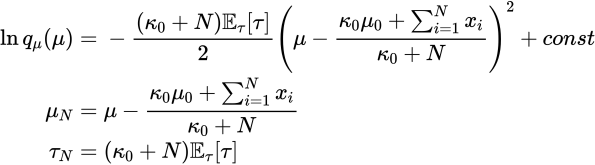
同様の作業を次は![]() について行います。
について行います。
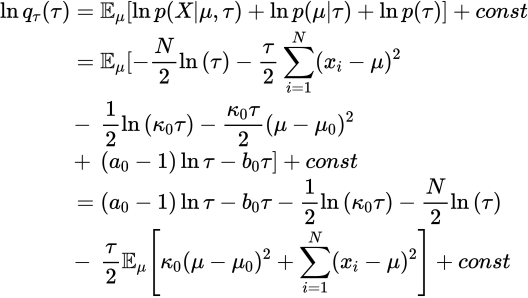
ガンマ分布に注意して
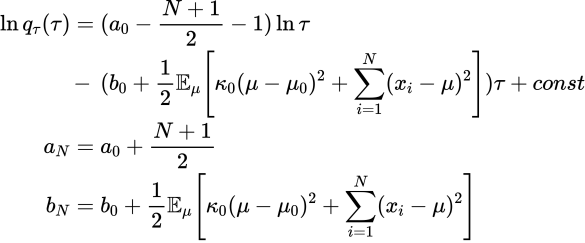
以上より
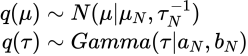
がわかりました。これより各期待値も簡単にもとまります。
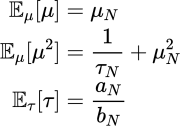
したがって
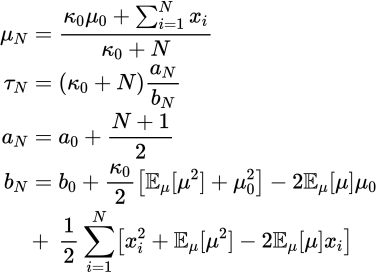
を用いて更新すればいいことがわかります。
もう一つの例として混合ガウス分布をVBを使ったEMで求める例がありますが、非常に難しいので詳しくは以下をご覧ください。
- https://github.com/vwrs/variational-gaussian-mixture/blob/master/variationalgaussianmixture.ipynb
- https://tips-memo.com/python-vb-gmm
応用
難しすぎて実装できませんでしたが変分ベイズを使った応用はたとえば自然言語処理におけるLDAがあります。とても難しい、、、、でわ
References
- https://stats.stackexchange.com/questions/271844/variational-inference-versus-mcmc-when-to-choose-one-over-the-other
- https://arxiv.org/pdf/1601.00670.pdf
- https://kaybrodersen.github.io/talks/Brodersen_2013_03_22.pdf
- https://qiita.com/kento1109/items/99a6bcbf18c1119d127c
- https://xyang35.github.io/2017/04/14/variational-lower-bound/
- https://www.colorado.edu/ASEN/asen5227_offline/slides/292-334.pdf
- http://www.math.kobe-u.ac.jp/HOME/higuchi/h18kogi/sect4.pdf
- https://www.iist.ac.in/sites/default/files/people/COVMain.pdf
- http://bjlkeng.github.io/posts/variational-bayes-and-the-mean-field-approximation/
- https://www.slideshare.net/takao-y/ss-28872465
- https://en.wikipedia.org/wiki/Normal_distribution
- https://openbook4.me/projects/261/sections/1648
- https://www.slideshare.net/takao-y/ss-28872465
- https://www.slideshare.net/tsubosaka/prml-10-1