こんにちは。
今回は前回のバンディットアルゴリズムの続きです。UCBと簡単なトンプソンサンプリングの実装を行います。前回実装した![]() -GreedyとBoltzmann Softmaxとの最終的な比較も行います。
-GreedyとBoltzmann Softmaxとの最終的な比較も行います。
Keywords
この記事のキーワードを先にリストアップします。
 -Greedy
-Greedy- Boltzmann Softmax
- Hoeffding’s inequality
- UCB
- Bayesian UCB
- Thompson Sampling
- scaled inverse chi-squared Distribution
先頭2つは前回やったので3つ目から話します。
Hoeffding’s inequality
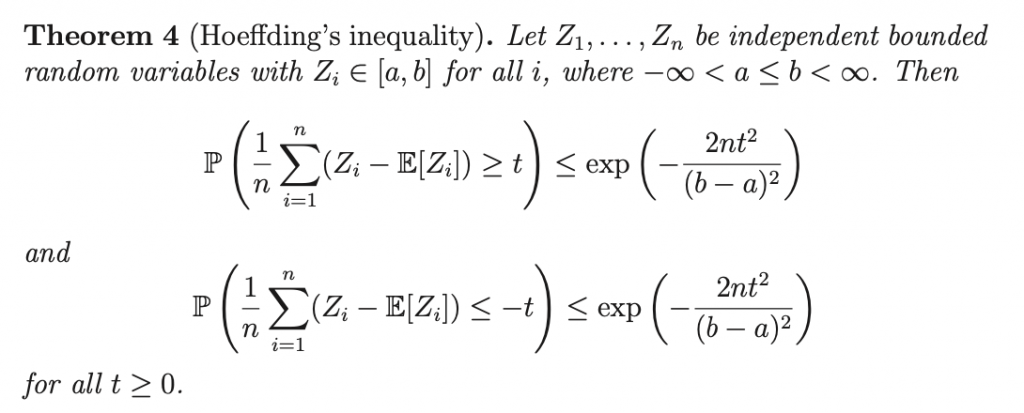
Hoeffdingの不等式です。これはUCBの導出に使います。証明にはマルコフの不等式とチェビシェフの不等式を使います。まあそれは置いておいて、この不等式の意味を考えます。
確率変数![]() の平均とその期待値の誤差
の平均とその期待値の誤差![]() の確率を
の確率を![]() で測っています。これがまさに後述するUCBの核の考え方です。こちら側で
で測っています。これがまさに後述するUCBの核の考え方です。こちら側で![]() そ操作することで、期待値のブレの許容範囲をある確率の範囲で操作することができます。
そ操作することで、期待値のブレの許容範囲をある確率の範囲で操作することができます。
UCB
UCBはアームの期待値に加えてその上限(Upper Confidence Bound)、いわばアームの可能性(分散)、を考慮したアルゴリズムです。どうやって上限を加味するかといいますと、対象のアームを選択した回数の逆数で重み付けします。こうすることで多数引いたアームにはより小さい上限を、少数引いたアームにはより大きい上限を付与することができます。
これは直感的にもいいですよね。何度も引いたことのあるガチャガチャよりも数回しか引いたことのないガチャガチャの方が可能性を感じますよね。そういうことです。
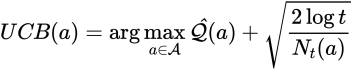
ただし、
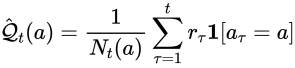
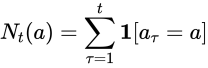
見ての通り、分母![]() が小さいほど大きい値が加算されます。イメージは次の感じです。
が小さいほど大きい値が加算されます。イメージは次の感じです。
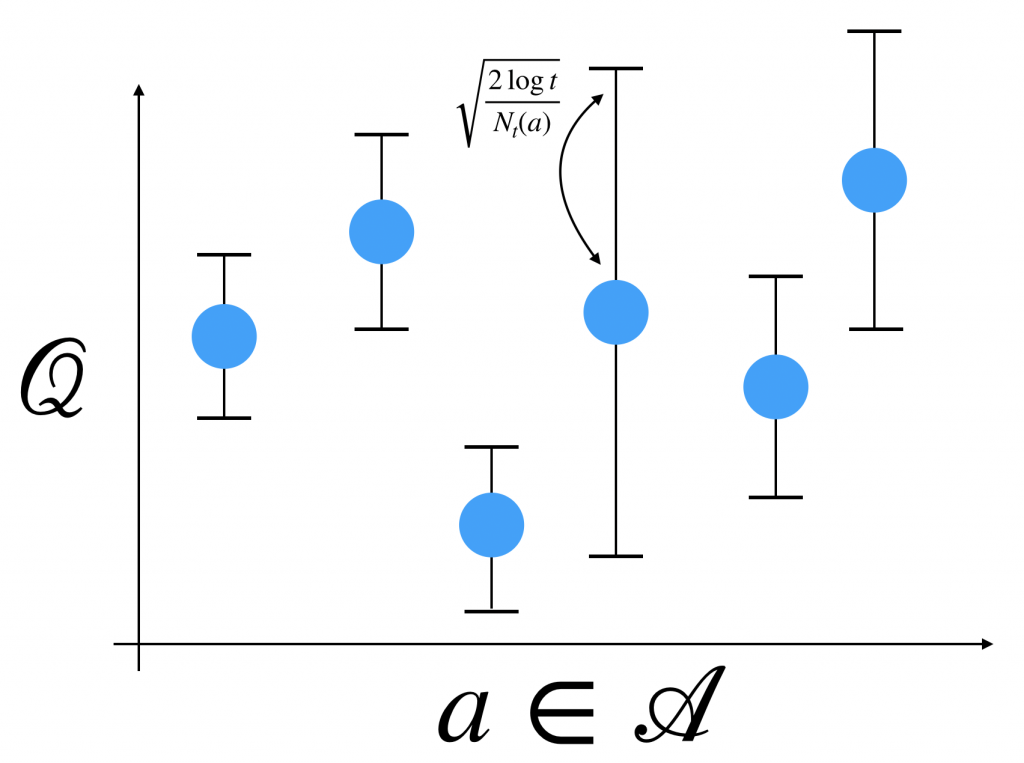
お気づきかもしれませんが逆数と言いつつ、ルートを付けてます。気になりますよね。ということで証明します。先程のHoeffdingの不等式を用います。
Hoeffdingの不等式において![]() を
を![]() として次が得られます。(
として次が得られます。(![]() )。報酬はベルヌーイを仮定しました。
)。報酬はベルヌーイを仮定しました。
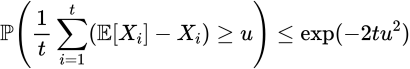
![]() を一つとり固定します。私たちの問題に書き換えるためNotationを定義します。
を一つとり固定します。私たちの問題に書き換えるためNotationを定義します。
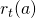 報酬(確率変数)
報酬(確率変数)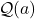 を真の行動価値
を真の行動価値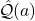 を経験上の行動価値
を経験上の行動価値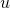 をupper confidence bound,
をupper confidence bound, 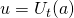
代入しますと
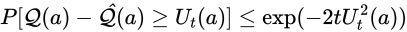
ここで上限に対する閾値をこちらで設定します。
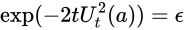
これを![]() に関して解けば終了です
に関して解けば終了です
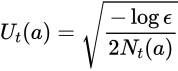
おや?よくみると2の位置が異なります。それは![]() をこちらで設定する必要があるからです。confidence levelと言われます。
をこちらで設定する必要があるからです。confidence levelと言われます。
UCBはこのconfidence levelをパラメータとして持ちます。もっとも一般的な値は次のようになります。
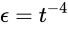
そしてこの時のアルゴリズムをUCB1いいます。代入して計算すると
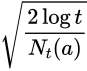
先程の結果になりました。では実装してみます。
実はよくない結果です。前回のEGとBSと比べるとわかります。この記事の最後に全アルゴリズムの比較を行いますのでとりあえずは進めていきます。
Bayesian UCB
UCBにベイズを応用したアルゴリズムのことです。今までは報酬の分布にベルヌーイを仮定しましたが、他にもガウス分布の仮定があります。それぞれ次のように呼びます
- Bernoulli – Thompson Sampling
- Gaussian – Thompson Sampling
察しの通り事後分布からパラメータをサンプリングしてアームを選択します。
本当にハードなんですが、Gaussianの場合の詳しい計算は
この方がやってくれています。
Thompson Sampling
定義は少し複雑ですが、実装の際はサンプリングを行うので思ったよりはシンプルです。
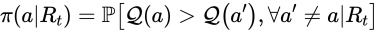
とある![]() が他のどの
が他のどの![]() よりも価値が高い、という事後確率(
よりも価値が高い、という事後確率(![]() )を計算して
)を計算して![]() を選ぶアルゴリズムです。
を選ぶアルゴリズムです。![]() は時刻tまでのアームのhistoryです。
は時刻tまでのアームのhistoryです。
事後確率は積分を用いて次のように計算されます。
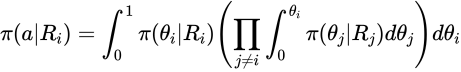
ここで![]() は
は![]() の報酬履歴です。左の積分が
の報酬履歴です。左の積分が![]() になる確率で右の積分がその他のアームで
になる確率で右の積分がその他のアームで![]() となる確率です。積分が解析的ではないので、サンプリングします。困ったときはサンプリングです。結果アルゴリズムは次のように単純化できます。
となる確率です。積分が解析的ではないので、サンプリングします。困ったときはサンプリングです。結果アルゴリズムは次のように単純化できます。
- 各アーム
 の報酬の期待値に関する事後分布
の報酬の期待値に関する事後分布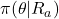 から乱数
から乱数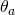 を生成
を生成 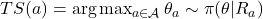
何度も言いますが報酬の分布はベルヌーイを仮定するので事後分布であるベータ分布は非常にシンプルになります。
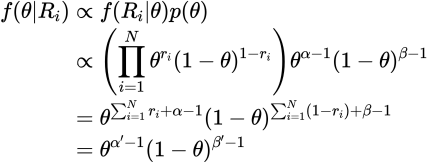
実装では一様分布を仮定するのでパラメータは共に1とします。
Best Arm RateをUCBと比較してみます。
全アルゴリズムでBARとCumulative Rewardsも比較してみます。
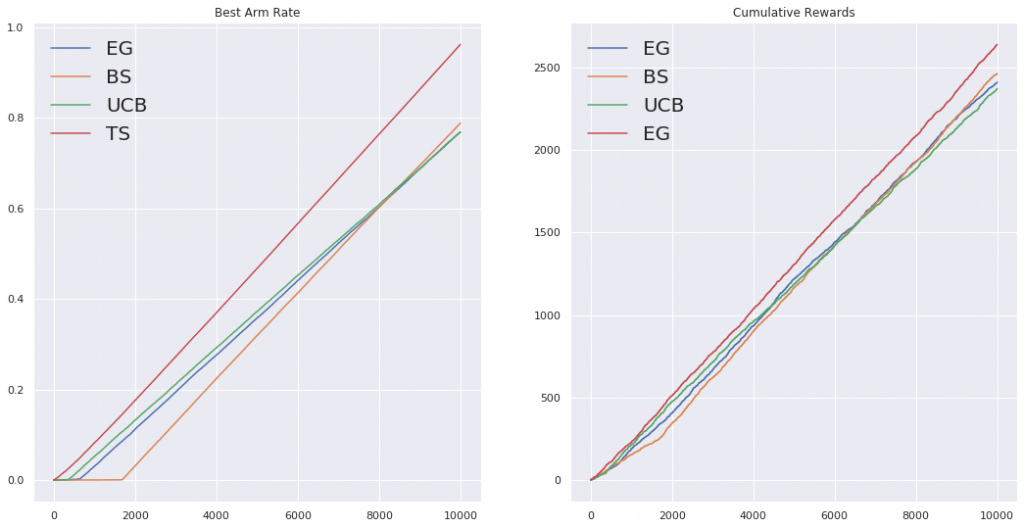
Thompson Samplingが圧勝でした。
scaled inverse chi-squared Distribution
もしGaussianでThompson Samplingを実装するならばこちらを![]() の事前分布として導入します。(事前分布
の事前分布として導入します。(事前分布![]() を条件付き確率で分解する)scaled inverse chi-squared分布といいます。
を条件付き確率で分解する)scaled inverse chi-squared分布といいます。
![]()
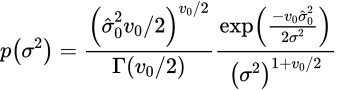
Code
Gaussian Thompson Samplingすごく難しいですね、パラメータが多すぎてなにがなんだが、、、
次回はContextual BanditとIPSについてまとめたいと思います。でわ
References
- https://youtu.be/xN11-epRuSU
- https://youtu.be/TIlDzLZPyhY
- http://snap.stanford.edu/class/cs246-2013/slides/18-bandits.pdf
- https://lilianweng.github.io/lil-log/2018/01/23/the-multi-armed-bandit-problem-and-its-solutions.html
- https://courses.cs.washington.edu/courses/cse599i/18wi/resources/lecture10/lecture10.pdf
- https://hagino3000.blogspot.com/2016/12/linear-bandit.html
- https://www.slideshare.net/tsubosaka/introduction-contexual-bandit
- http://ibisml.org/archive/ibis2014/ibis2014_bandit.pdf
- http://seetheworld1992.hatenablog.com/entry/2017/06/04/150253
- https://to-kei.net/bayes/bayes-normal-distribution/