こんにちは。
標準化は機械学習において非常に重要な概念です。スケール統一のためや学習速度の向上を目的に使われます。そこで今回は多変量ガウス分布の標準化などをやっていこうと思います。数式やいろんな公式が現れますが知らないものがあれば調べながら読むことをお勧めします。
定理
ある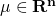 と
と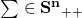 に対して
に対して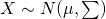 とすると、
とすると、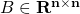 が存在し次を満たす、
が存在し次を満たす、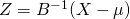 とすると
とすると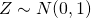
- 共分散行列
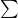 がある正則行列
がある正則行列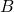 を用いて
を用いて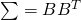 と分解できる(コレスキー分解)
と分解できる(コレスキー分解) 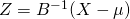 を用いて
を用いて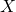 から異なるベクトルランダム変数
から異なるベクトルランダム変数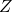 を作る
を作る
ではまず、おなじみのLinear Algebraです。対称行列に関する以下の2つの性質
- 任意の実対称行列
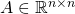 は常に
は常に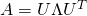 で表される、ここで
で表される、ここで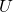 はfull-rank直行行列であり、その列に
はfull-rank直行行列であり、その列に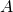 の固有ベクトルを持ち
の固有ベクトルを持ち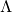 は
は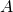 の固有値を持つ対角行列である
の固有値を持つ対角行列である - もし
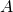 が正定値対称行列なら、すべての固有値は正である
が正定値対称行列なら、すべての固有値は正である
共分散行列
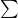
は正定値なので1つ目の性質を使うことによりある適当な行列
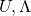
を用いて
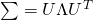
と書けます。また、2つ目の性質を使うことにより
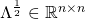
を
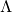
の各要素の二乗根に対応する要素として持つ対角行列とできます。
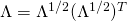
なので代入すると
![Rendered by QuickLaTeX.com \[\sum = U\Lambda U^T = U\Lambda^{1/2}(\Lambda^{1/2})^TU^T = U\Lambda^{1/2}(U\Lambda^{1/2})^T = BB^T\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-3d4bd9ee0b9dc19bf1638473a61f000d_l3.png)
となります。ただし
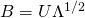
としました。余談ですが僕が今までやってきた中で知っておいたほうがいい分解をいくつかリストしておきます。
- 対角化
- 特異値分解(SVD)
- QR分解
- LU分解
- コレスキー分解
特に上の2つは重要ですね、対角化は昔紹介したPCAの応用編で重要な概念になります。話が少し外れましたが上の式変形はコレスキー分解です。
逆行列の公式により、
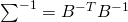
となるので多変量ガウス分布の式は次のように書き換えられます
![Rendered by QuickLaTeX.com \[P(x;\mu, \sum) = \frac{1}{(2\pi)^{n/2}|BB^T|^{1/2}}\exp{-\frac{1}{2}(x-\mu)^TB^{-T}B^{-1}(x-\mu)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-ce968c4c77b48b586ad82347bae4723b_l3.png)
多変量標準ガウスに近づいたことがわかると思います。ここでお分かりかもしれませんが新しい変数を
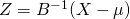
と定義します。
![Rendered by QuickLaTeX.com X = [X_1 \cdots X_n]^T \in\mathbb{R^n}](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-a0780517634c5354501177a834207735_l3.png)
が同時密度関数
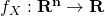
によるベクトル値ランダム変数と仮定します。もし
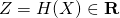
ただし
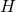
は全単射で微分可能関数なら
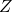
は次の同時密度関数
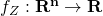
を持ちます。
変数変換式を用いることでベクトル変数
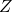
が次の同時密度を持つことがわかります。(ヤコビアンとかで調べてください。)
![Rendered by QuickLaTeX.com \[p_Z(z) = \frac{1}{(2\pi)^{n/2}}\exp(-\frac{1}{2}z^Tz)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-f48ea996c24c29bac6bc3c20421b220e_l3.png)
これはまさしく
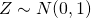
です。
定理を実験
上記の定理を実際に確認してみます。作業過程は次の通り
![Rendered by QuickLaTeX.com X\sim N(\mu,\sum),(\mu=[3,3]^T,\sum=diag(1,3))](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-d637297779dc0ac00eba176b41e51298_l3.png) を
を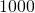 点作成する
点作成する- ここで作成したデータの平均
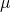 を計算しておく
を計算しておく - 次に定理の
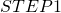 より共分散行列をコレスキー分解し
より共分散行列をコレスキー分解し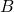 を求める
を求める
- 上記の
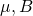 を用いて新たな確率変数
を用いて新たな確率変数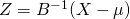 を作る
を作る - 作った各データ
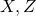 をscatter plotする
をscatter plotする
こんな感じになりまして。青の点が
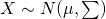
であり、赤の点が
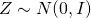
となっていることがグラフから大体わかります。実際に出力させて確認してみてください。
データ変換行列Wとの関係
上ではどちらかというとデータを戻すという動作を行いました。いえ、標準化を戻すということにしておきます。次に標準化されたデータを変換し、その変換行列の性質を見ていきたいと思います。
今、三次元標準ガウス分布に従うデータZが1000点あるとします。そして、これを二次元に移す変換Wをかけた時のデータWZとWの関係を考察しましょう。たとえば
とういう変換をかけた場合、
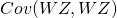
の固有ベクトルは
の各列ベクトルであり固有値は
![Rendered by QuickLaTeX.com [ 55.27931408~,~4.49399939]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-fffb0d6781ded50b54fdef841146143a_l3.png)
です。ここでWの特異値分解
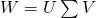
を見てみます
この通り
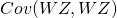
の固有ベクトルはUの各列ベクトルに、固有値は特異値の平方に近い値になっていますね。数式を用いて確認してみましょう。Wの特異値分解を
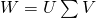
とし、
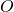
は適当な零行列です
![Rendered by QuickLaTeX.com \[WW^T = U\sum VV^T{\sum}^TV^T = U\sum{\sum}^TU^T\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-f0914956375239d4667eb3f400e54385_l3.png)
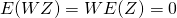
であり
これより上記の予想が正しかったことがわかります。
特異値分解の関係
まず
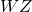
の共分散行列
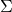
を対角化し
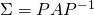
となったとします。ここで線形変換行列
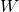
は
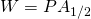
としておくと。ただし、
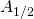
の各成分は行列
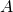
のそれぞれの成分の正の平方根。
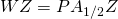
の共分散を求めると
となります。つまり、
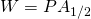
とすることで,この形の共分散が達成されることがわかります。
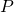
が直交行列であることを忘れずに。次に
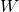
の特異値を求めます。
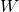
の特異値は
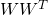
の固有値の正の平方根です。まず
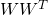
を計算すると
![Rendered by QuickLaTeX.com \[WW^{T} = PA_{1/2} A^{T}{1/2}P^{T} = PAP^{T}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-dd0c30e3317bcb85fa98d89b415e82df_l3.png)
これは
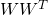
の対角化そのものであるので
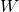
の特異値は
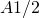
の対角成分となり、
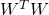
の固有値は
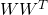
の固有値と一致するので
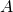
の対角成分となります。つまり、
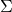
の固有値の平方根が
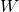
の特異値となるんです。
対角化と特異値分解は奥が深いですね。ちなみに最近パソコンがかなり暑くなって調子が悪いです。でわ。
Reference
と
に対して
とすると、
が存在し次を満たす、
とすると
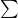 がある正則行列
がある正則行列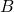 を用いて
を用いて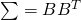 と分解できる(コレスキー分解)
と分解できる(コレスキー分解)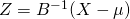 を用いて
を用いて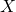 から異なるベクトルランダム変数
から異なるベクトルランダム変数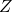 を作る
を作る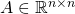 は常に
は常に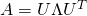 で表される、ここで
で表される、ここで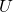 はfull-rank直行行列であり、その列に
はfull-rank直行行列であり、その列に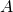 の固有ベクトルを持ち
の固有ベクトルを持ち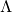 は
は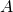 の固有値を持つ対角行列である
の固有値を持つ対角行列である が正定値対称行列なら、すべての固有値は正である
が正定値対称行列なら、すべての固有値は正である![]()
![]()
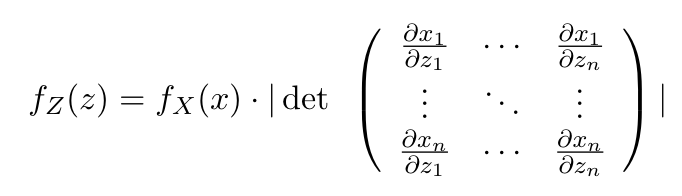
![]()
![Rendered by QuickLaTeX.com X\sim N(\mu,\sum),(\mu=[3,3]^T,\sum=diag(1,3))](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-d637297779dc0ac00eba176b41e51298_l3.png) を
を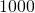 点作成する
点作成する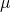 を計算しておく
を計算しておく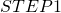 より共分散行列をコレスキー分解し
より共分散行列をコレスキー分解し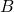 を求める
を求める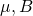 を用いて新たな確率変数
を用いて新たな確率変数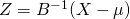 を作る
を作る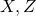 をscatter plotする
をscatter plotする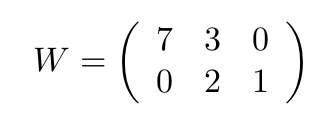
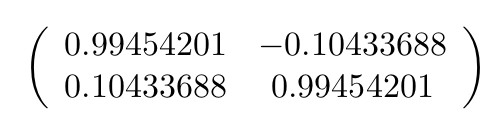

![]()
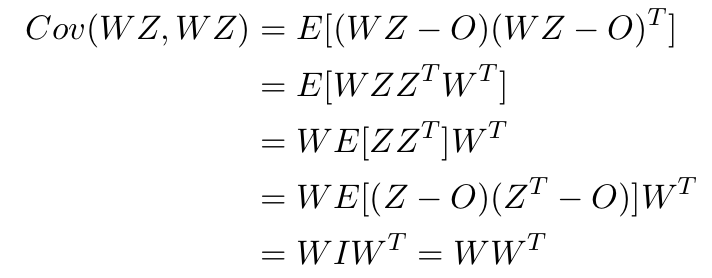
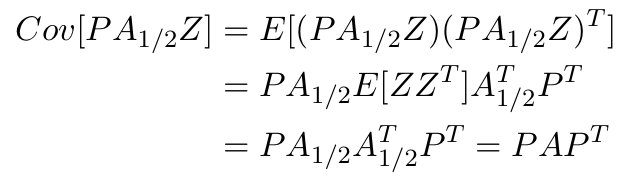
![]()