本日はEMアルゴリズムについてお話ししようと思います。「EMアルゴリズム?」と思った方へ先に簡単に紹介すると
Expectation-Maximization Algorithm
の略で、潜在変数(Z)を用いて、iterativeに尤度最大化を行う手法です。iterativeというのはE-step、M-stepと言われる2種類を交互に行い尤度を最大化し、パラメータを決定します。2ステップに分けて行うことがミソなんですけれど数式ゴリゴリすると途中で自分が何をやっていたかわからなくなるんですよね。その点に注意しながら進めていこうと思います。Notation
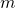 個の独立なデータ(observable)、
個の独立なデータ(observable)、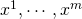
- モデルのパラメータ、
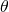
- 潜在変数(unobservable)、

![Rendered by QuickLaTeX.com \[l(\theta) = \sum_{i=1}^{m} \log p(x^{i};\theta) = \sum_{i=1}^{m}\log \sum_{z}^{}p(x^{i},z;\theta)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-e14c8b7e1b6447ec3f880ef780a09860_l3.png)
![Rendered by QuickLaTeX.com \[= \sum_{i}^{}\log\sum_{z^{(i)}}^{}Q_i(z^{(i)})\frac{p(x^{i},z^{(i)};\theta)}{Q_i(z^{(i)})}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-707c2f13fa25a463dd246c7b1a588856_l3.png)
![Rendered by QuickLaTeX.com \[\geq \sum_{i}^{}\sum_{z^{(i)}}^{} Q_i(z^{(i)})\log\frac{p(x^{i},z^{(i)};\theta)}{Q_i(z^{(i)})}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-3383e605e646dac5b117a4d3f4f7d2f2_l3.png)
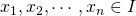
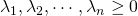
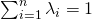 ,
,
![Rendered by QuickLaTeX.com \[f\left (\sum_{i=1}^{n}\lambda_i x_i\right) \leq \sum_{i=1}^{n}\lambda_if(x_i)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-ae594d8e85ac8499e15ba4ad4e4030b9_l3.png)
![Rendered by QuickLaTeX.com \[In\sum_{i=1}^{n} \lambda_i x_i \geq \sum_{i=1}^{n} \lambda_i In(x_i)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-27cfcaae502afcc9541e92353afb58d2_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{p\left(x^{i}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)}=constant\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-cc24d76cb802a6cb7643feee93485f84_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \theta :=\arg \max_{\theta} \sum{i} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{p\left(x^{i}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-1b56b4942df4daceb0dfd623b4eff6ec_l3.png)
- 潜在変数
 の事後確率計算
の事後確率計算 - パラメータ
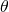 の更新
の更新
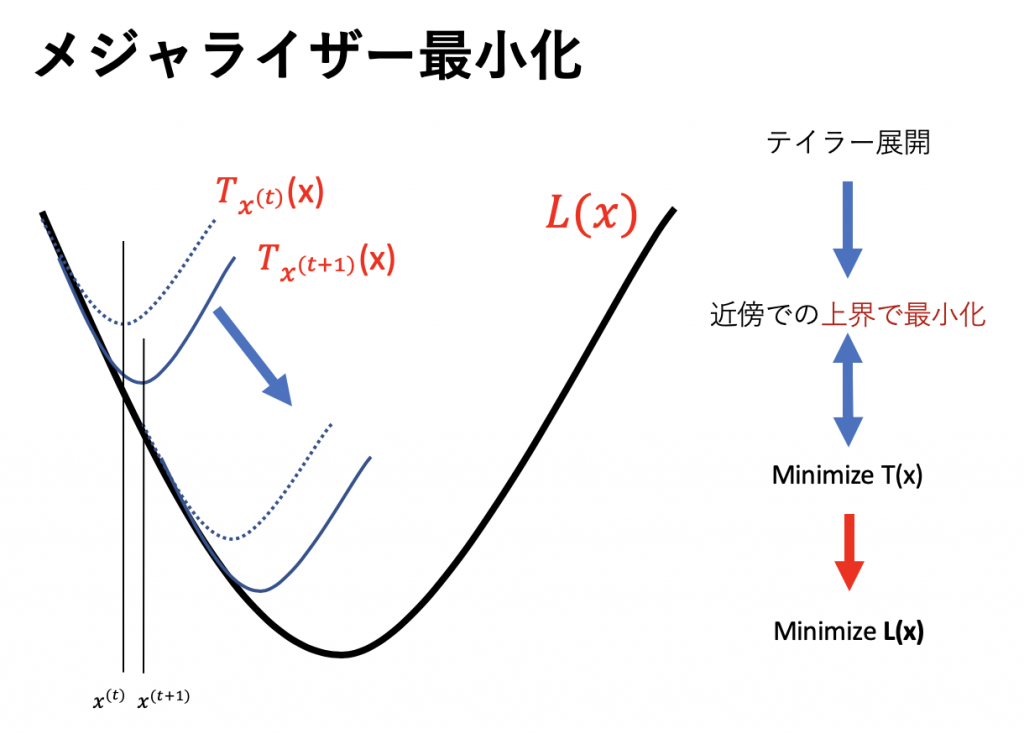
では、コレで下界の最大化ができたことになりますがその際、本来の目的関数、つまり
![Rendered by QuickLaTeX.com \[ l\left(\theta^{(t)}\right)=\sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{i}, z^{(i)} ; \theta^{(t)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-826673014936930e1eae3a7d56b85046_l3.png)
![Rendered by QuickLaTeX.com \[ l\left(\theta^{(t+1)}\right) \geq \sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{i}, z^{(i)} ; \theta^{(t+1)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-618022ae2174bc0d388e9769bfc6fb5f_l3.png)
![Rendered by QuickLaTeX.com \[ \geq \sum_{i} \sum_{z^{(i)}} Q_{i}^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{i}, z^{(i)} ; \theta^{(t)}\right)}{Q_{i}^{(t)}\left(z^{(i)}\right)} = l(\theta^{(t)})\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-f765bc6e28220507ffd737ff9e487ed3_l3.png)
EMとKL
先ほどのこの式 ![Rendered by QuickLaTeX.com \[ \sum_{i} \log p\left(x^{i} \theta\right) \geq \sum_{i} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{p\left(x^{i}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-dce1249154d83359da34dd15b1ff0ce0_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
今回はEMアルゴリズムをもとに数式をずらずらとやってみました。日本の大学はレジュメも講義もほとんど公開してないですね、、
References
- https://www.cs.utah.edu/~piyush/teaching/EM_algorithm.pdf
- http://www.princeton.edu/~amirali/Public/Teaching/ORF523/S16/ORF523_S16_Lec7_gh.pdf
- http://pianopiano.sakura.ne.jp/ml/em-algorithm/
- https://oimeg.blogspot.jp/2015/07/em.html
- https://en.wikipedia.org/wiki/Convex_function
- https://mathtrain.jp/jensen_proof
- http://cs229.stanford.edu/notes/cs229-notes8.pdf
- https://math.stackexchange.com/questions/628386/when-jensens-inequality-is-equality
- https://qiita.com/kenmatsu4/items/59ea3e5dfa3d4c161efb
- https://math.stackexchange.com/questions/247795/what-is-the-covariance-of-mixture-bernoulli-distribution