こんにちは。
少し前に標準化・正規化についてお話ししました。これらは勾配法による学習の際に学習速度が速くなるというメリットがありました。では今回は
正則化とはなんぞや
名前が似てますね、ということは
勾配法に関係あり?学習速度に関係あり?
いい読みです。次の図を見てください。
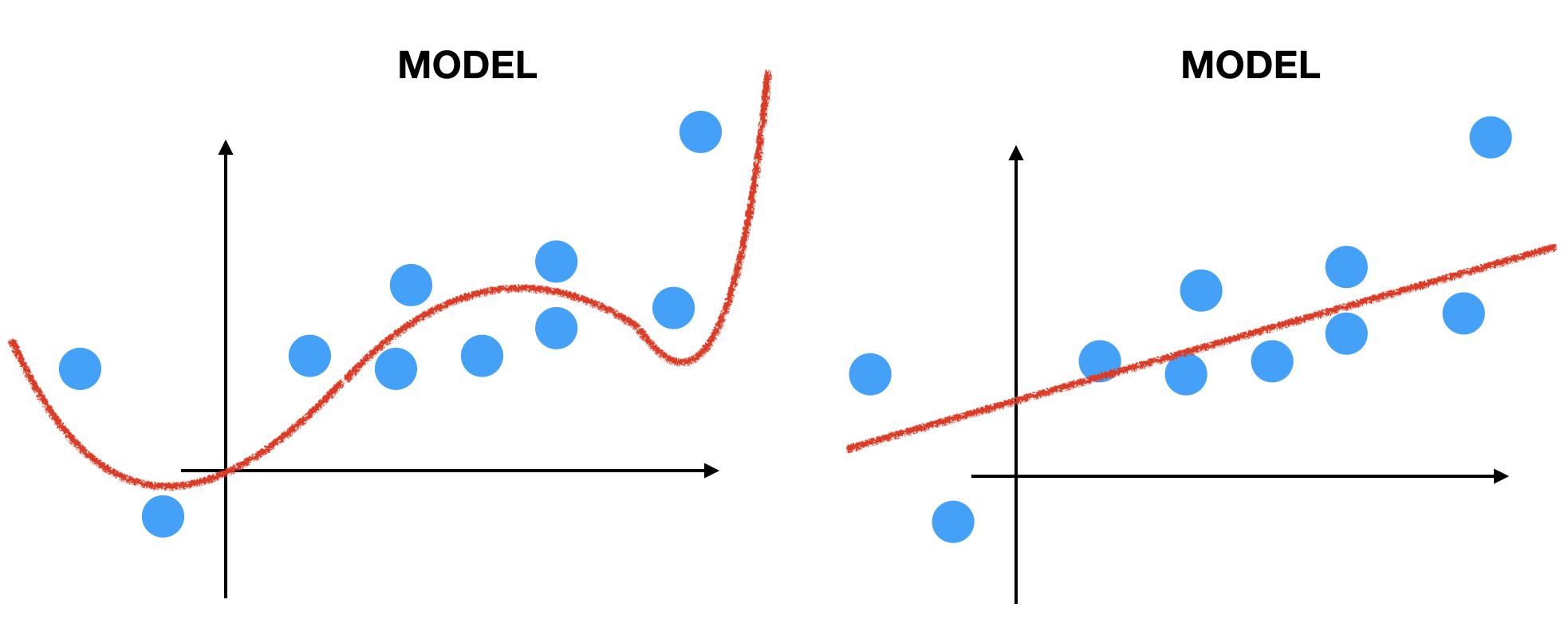
どっちの曲線が「いい学習」をした結果だと思いますか? もう一問
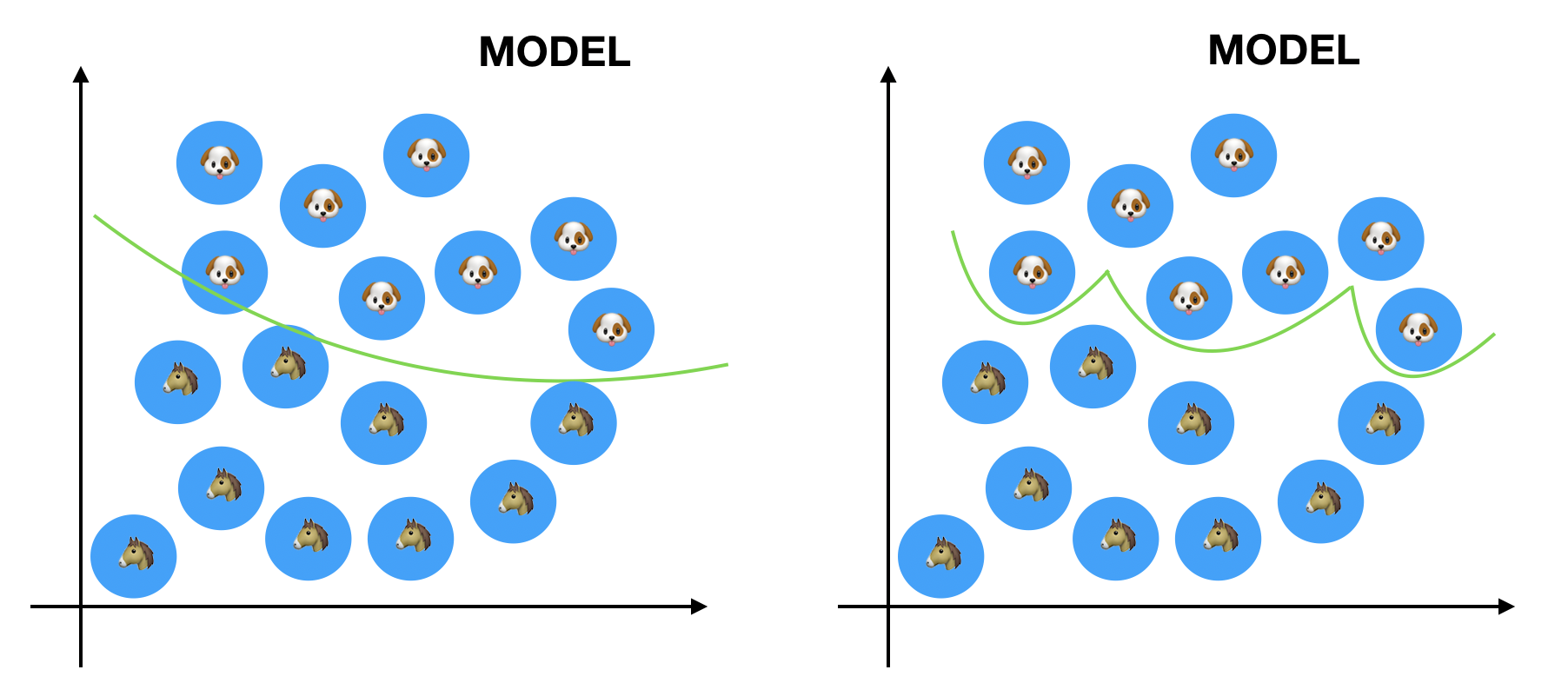
どちらが「いい分類」をしていますか?
「いい分類・いい学習」とは何か?
を考える必要があります。データには誤差がつきものです。なので「誤差を許容するという寛大な心が必要」なんです。つまり、
モデルは柔軟性を持つべき
という考えから「正則化」とう考えに突入します。
具体的には?
そもそもなんで過学習してしまうのか、ですよね。
あるモデルが過学習するということはパラメータが手持ちのデータを重視しすぎるということ
言い換えると
過学習とはモデルが未知のデータを考慮しなくなるということです。
このままではいけません。未知のデータを考慮させる必要があり、そのための作戦が「正則化」です。具体的には
パラメータの学習に制限を設けること
です。例えば、パラメータ![]() を学習させたいとします。そこでモデルを
を学習させたいとします。そこでモデルを![]() 、ラベルを
、ラベルを![]() とでもし
とでもし
![]()
を最小化することで![]() を学習させる問題を考えます。このままやると
を学習させる問題を考えます。このままやると![]() は好き放題学習しますが
は好き放題学習しますが![]() で
で
![]()
とかのように制限設けると![]() はこの範囲で学習しますよね。しかしこれは考える問題が
はこの範囲で学習しますよね。しかしこれは考える問題が
![]()
から
![]()
のように制約付きの最適化問題になりました。ヤバイ、しかも
制約が不等式!!!
これはやばいです。しかし!
KKT条件という物を使えば解決します。(ちなみにSVMとかでも出てきますがかなり難しいです)(ちなみに制約が等式の時はラグランジュの未定乗数法)つまり![]() で
で
![]()
とできます。ただし![]() はLpノルムです。
はLpノルムです。
Lpノルムって何?
![]() とします、つまり
とします、つまり![]() はn次元実ベクトルとします。この時
はn次元実ベクトルとします。この時![]() に対して
に対して
![]()
と定義します。これを![]() のLpノルムと言います。関数解析でやるので覚えといて〜。初めての人は直感がわかないと思うので図で見てみましょう。
のLpノルムと言います。関数解析でやるので覚えといて〜。初めての人は直感がわかないと思うので図で見てみましょう。
一般的に使うのは![]() です。少し話が逸れましたが
です。少し話が逸れましたが
![]()
これですね。コスト関数を最小化する際に![]() が大きくならないようにペナルティーの形で加えます。なので第二項は罰金項、正規化項などと呼ばれます。これを使った実際の例は次の2つがあります。
が大きくならないようにペナルティーの形で加えます。なので第二項は罰金項、正規化項などと呼ばれます。これを使った実際の例は次の2つがあります。
- Ridge Regression (Tikhonov regularization)
- Lasso Regression
です。リッジ回帰は![]() 正規化項を使います。なので
正規化項を使います。なので
![]()
となります。一方でラッソ回帰は![]() 正規化項を使います。なので
正規化項を使います。なので
![]()
です。これらについて詳しくは別の記事で書きます。今はとりあえず「正則化」の例として覚えておいてください。
さて、正則化はパラメータの学習に制限を設けることと言いました。で、各ノルムに対する正規化項の特徴についてです。がこれも長くなるので次の記事で会いましょう。
でわ。
READMORE