こんにちは。
本日は勾配法の実装です。まずは軽く復習しましょう。まず勾配とは関数の変化量が最も大きい方法でしたね。
そして勾配法とは勾配を用いて目的関数の極値を探る方法でした。最終的に得られるのは学習させたいパラメータです。
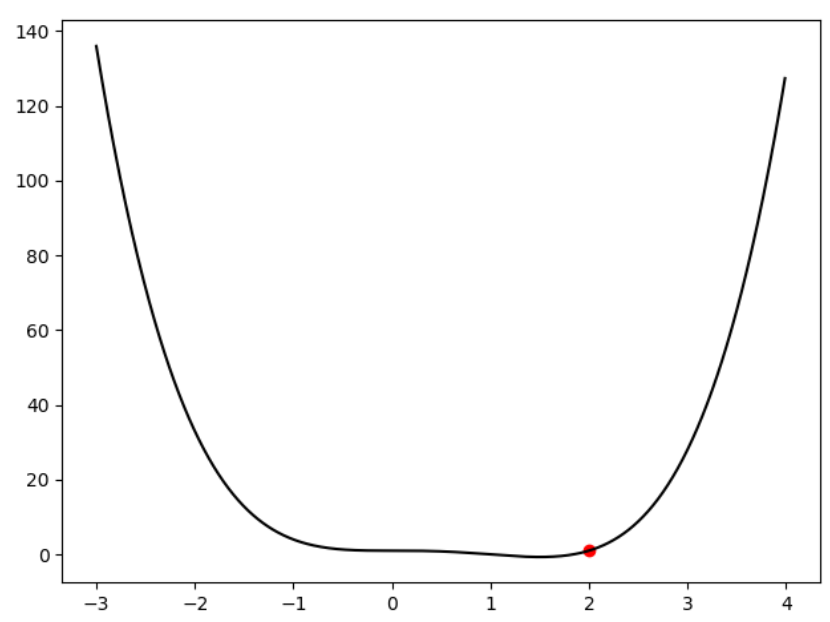
今回は次の関数を目的関数とします。可視化を簡単にするため一変数関数を扱います。
![]()
さて今回の場合の勾配はただの微分です。なので![]() です。ちなみに微分って聞いたら差分法を忘れないでくださいね。
です。ちなみに微分って聞いたら差分法を忘れないでくださいね。
ではこれらを用いて次の式(勾配法)でxを更新します。
![]()
コードを書くときは上書きなので矢印はイコールになり、今回は最小化なので符号はマイナスです。さて、あとは初期値と学習率![]() を決めるだけです。今回は学習率を変えてその振る舞いを見ようと思います。xの初期値については
を決めるだけです。今回は学習率を変えてその振る舞いを見ようと思います。xの初期値については![]() としました。(上の図の赤い点が初期値、つまりスタート地点)
としました。(上の図の赤い点が初期値、つまりスタート地点)
ではPythonでサクッと実装すると異なる学習率に対して次のような結果になりました。
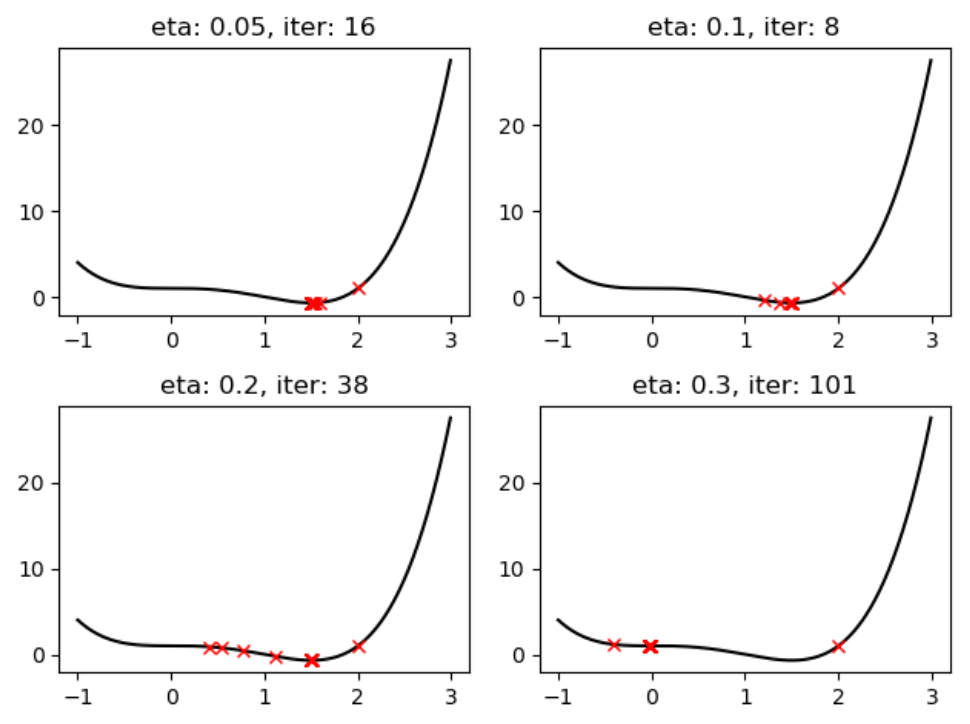 ペコっとなった
ペコっとなった![]() あたりで収束し極値を取っています。ここで注目してもらいたいのが右下の図です。
あたりで収束し極値を取っています。ここで注目してもらいたいのが右下の図です。
この図では![]() あたりで収束しています。おっと?これは前言った最適解ではなく局所解です。これをxの軌跡を実際にみて確かめましょう。まず
あたりで収束しています。おっと?これは前言った最適解ではなく局所解です。これをxの軌跡を実際にみて確かめましょう。まず![]() の場合のxの軌跡は次の通りです。
の場合のxの軌跡は次の通りです。
2.0
1.2
1.3728000000000002
1.4686874222592001
1.4957044497076786
1.4995483345721634
1.4999545886920822
1.4999954563946214
望み通りの結果です。一方で右下(![]() )の場合のxの軌跡は
)の場合のxの軌跡は
2.0
-0.3999999999999999
-0.03520000000000012
-0.032917390950400104
-0.03092419127230648
-0.029167353608819366
-0.027606255069678485
-0.011492117223670599
-0.010192155321175003
-0.010003900753329536
-0.007953518077630905
-0.00783904911530178
-0.004808208102120086
ちょっと長すぎたんで中間切り取ったんですが言いたいことは1回目の更新で一気にズレすぎたんですね。そのせいで左にある窪みで収束してます。これは学習率を選択する際の問題です。理論編、で言ったものですね。
まあそんなことは置いておいてとりあえず勾配法の働きを可視化により理解できたかと思います。ではもう一つ考えてみましょう。
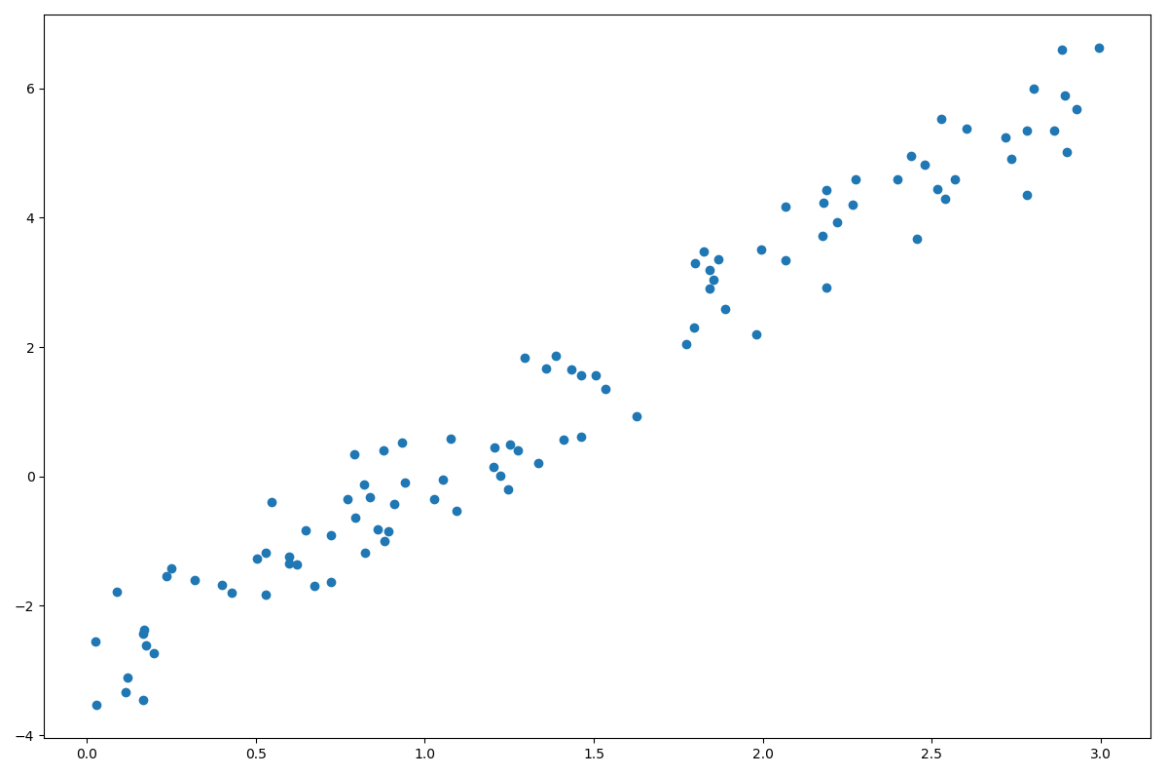
このプロットがソーセージだとしたらどのように棒をさせばフランクフルトになりますか?

答えは明らかですよね。ソーセージに平行にさせばいんです。
次回は「フランクフルトに棒をさす」について記事を書きます。キーワードは線形回帰です。
ではまた
質問、アドバイスよろしくお願いします。
参考: