こんにちは。
そもそも機械学習における学習とはなんなのか?
を少し考えてみましょう。まずはデータの形から

基本的にデータは![]() という行列で表されます。この時にデータは縦並びが基本だと思います。では、例えば「何かの分類」をしたい時を考えます。もっと具体的に目標を考えてみましょう。
という行列で表されます。この時にデータは縦並びが基本だと思います。では、例えば「何かの分類」をしたい時を考えます。もっと具体的に目標を考えてみましょう。
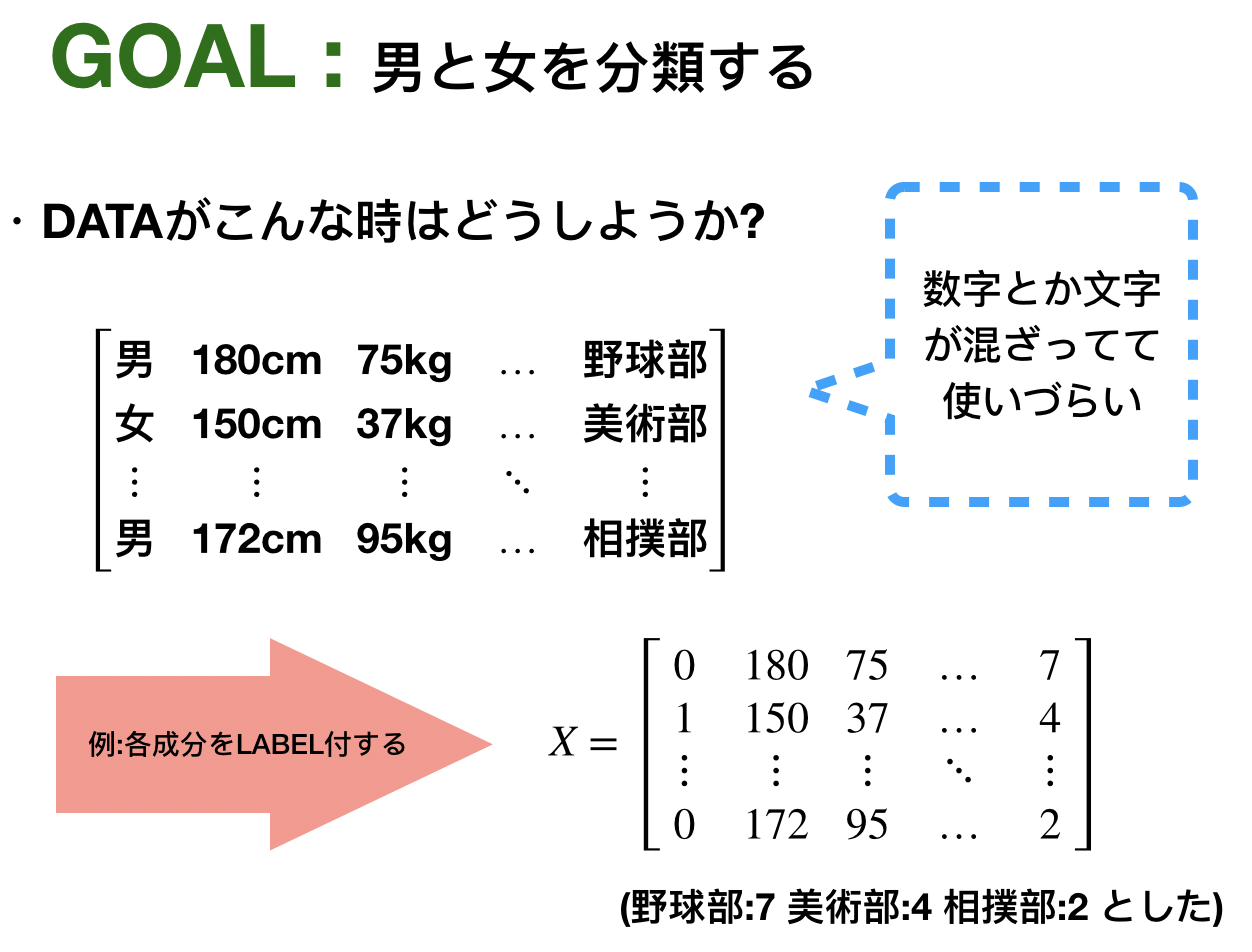
今の目標は男女の分類です。今回の学習では正解が必要になります。なのでデータに正解のラベルを0,1として組み込んでいます。では次は分類を判別するモデルが必要ですね。これは次のようなイメージです。
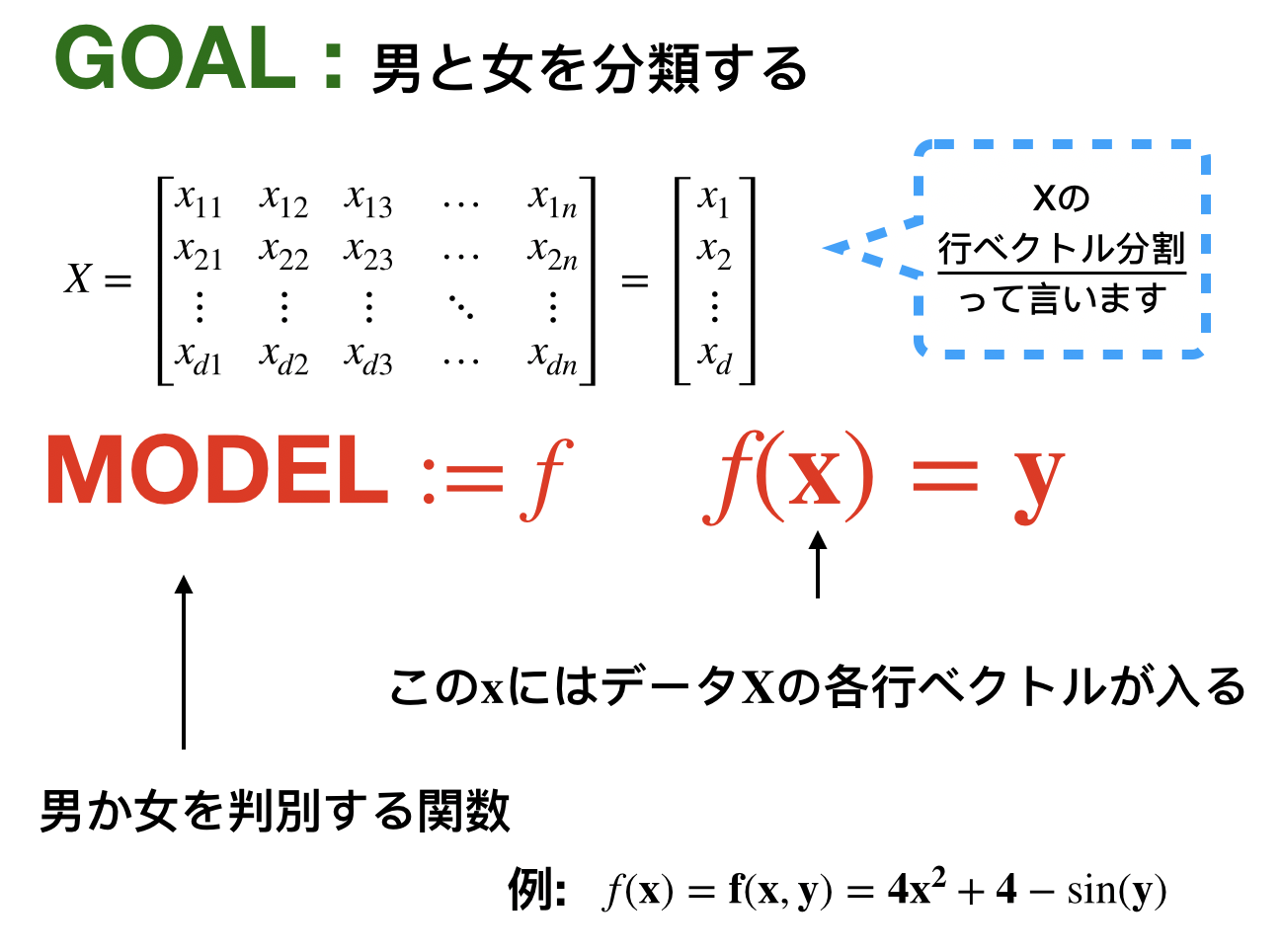
データの準備はOK,モデルもOK,![]() の動きを確認しよう
の動きを確認しよう
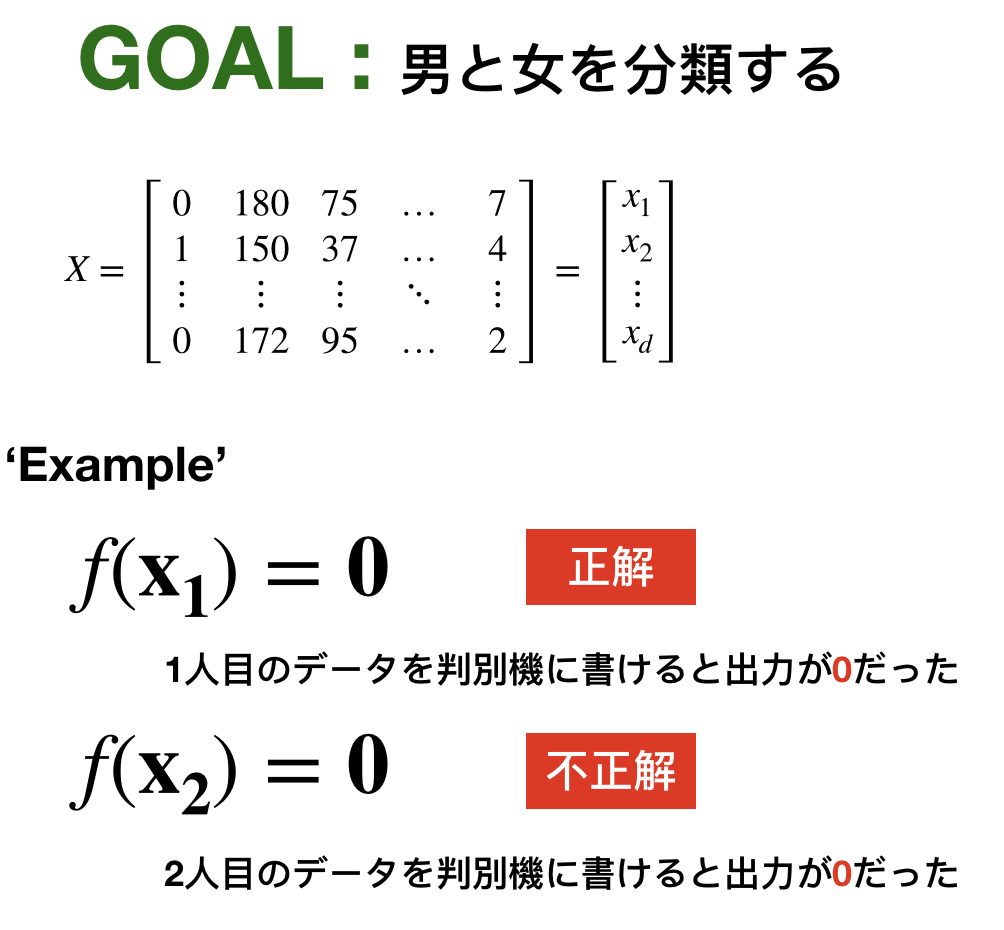
![]() がうまく判別できていないですね。どうしましょうか?ここからが学習!
がうまく判別できていないですね。どうしましょうか?ここからが学習!
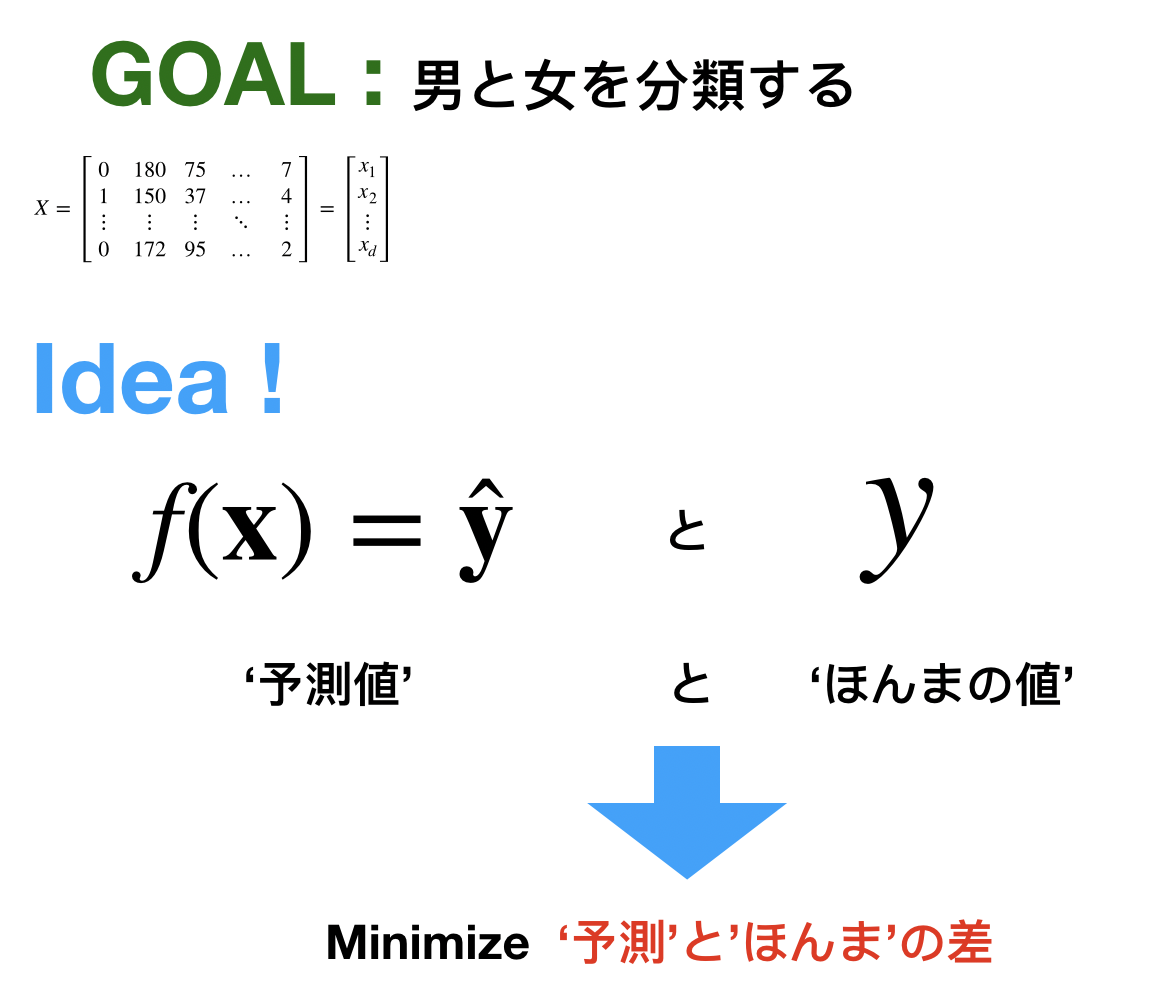
ズバリ一言でまとめると
誤差が最小になるようにすることが学習です
ここまではとても直感的な説明でした、では最後の赤文字について話していきます。
mean squared error
聞いたことありませんか?機械学習をちょっとでもしてる人なら初見ではないと思います。(ちなみに上の赤字の部分をerrorとよく言います。)数式だと次のような形です。
![Rendered by QuickLaTeX.com \[\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2 \]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-b29b9e864f0f84d14782b3de820b1e37_l3.png)
記号の説明をしますと、N個のデータに対してi番目の予測値を![]() 、対応する正解を
、対応する正解を![]() としています。ちなみに、
としています。ちなみに、![]() と言う表記がされていれば大抵は予測値のことを意味していると思います。よって与式は「平均二乗誤差」と言います。恐らくこれがもっともポピュラーなコスト関数でしょう。この値が小さくなればうまく予測できてると言うことになりますよね、なので機械学習では目的関数を定めてその最適化(この場合は最小化)を目的とします。
と言う表記がされていれば大抵は予測値のことを意味していると思います。よって与式は「平均二乗誤差」と言います。恐らくこれがもっともポピュラーなコスト関数でしょう。この値が小さくなればうまく予測できてると言うことになりますよね、なので機械学習では目的関数を定めてその最適化(この場合は最小化)を目的とします。
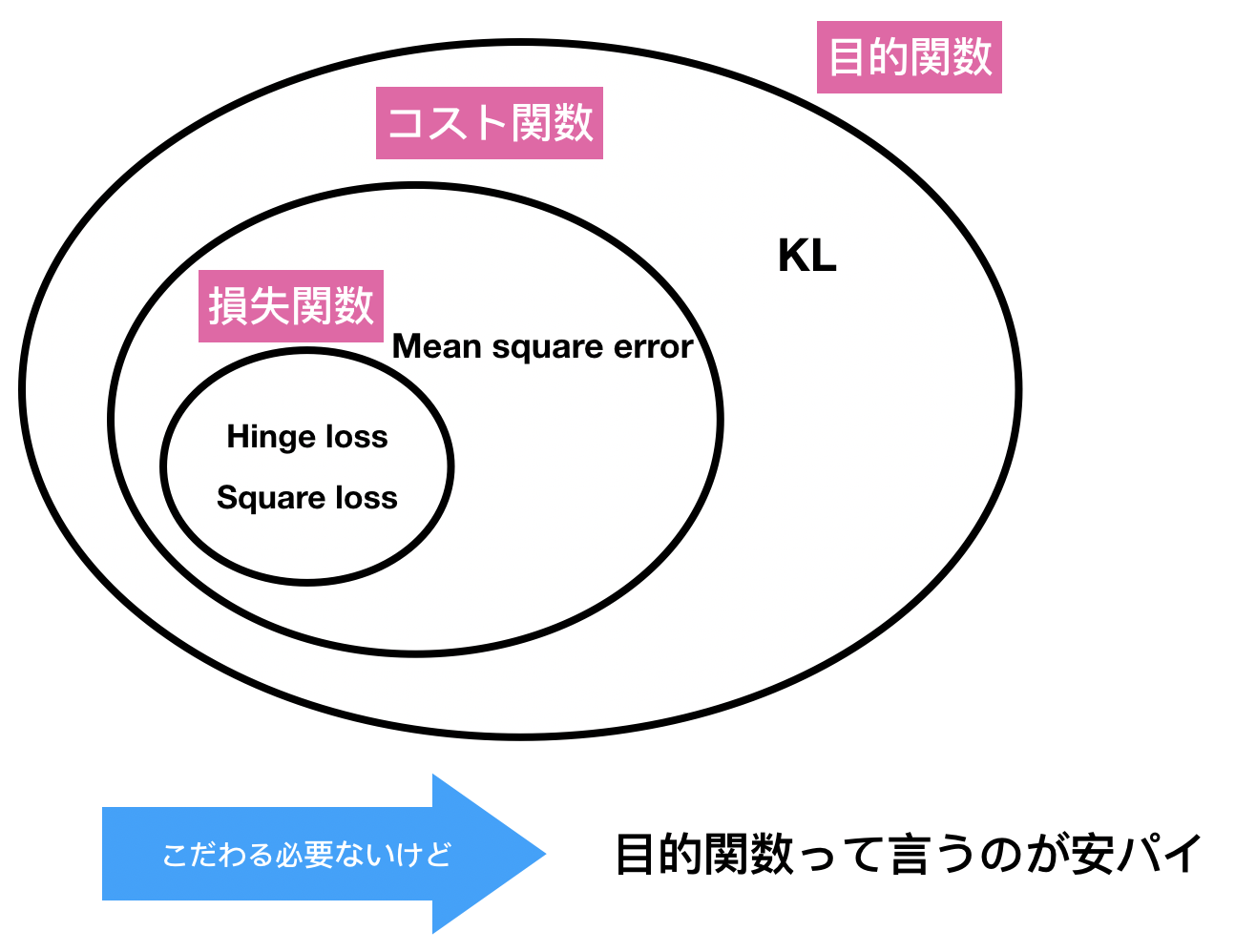
おっと、似た言葉が出てきました。機械学習では「損失関数」「コスト関数」「目的関数」の三つの類似用語があります。そんなに大きな差はないと思いますが一応整理しておきましょう。
-
損失関数 (loss function)
これはデータ点 ![]() 、予測
、予測 ![]() 、ラベル(正解)
、ラベル(正解) ![]() の元で定義される関数で次のようなものがあります。
の元で定義される関数で次のようなものがあります。
- square loss :
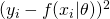 (よく見かける)
(よく見かける) - hinge loss :
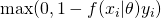 (SVMで見かける)
(SVMで見かける)
-
コスト関数 (cost function)
先ほどはデータ点1点に対しての定義でしたがこちらではトレーニングデータ、つまりデータの集合に関して定義します。
- Mean Squared Error :
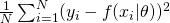
-
目的関数 (Objective function)
もっと広い意味で使われます。
- Divergence (KLとか)
では本題の学習についてですが、
学習についてもう少し踏み込みましょう
機械学習における学習はなんなんでしょうね。前述の例だと
「学習する」![]() 「平均二乗誤差を最小化する」
「平均二乗誤差を最小化する」
になります。
これを可視化してみましょう。の前に一つ大事なキーワード
パラメータって何?
これはモデルを定義する時に使われます。例えば![]() とするとパラメータは
とするとパラメータは![]() です。
です。
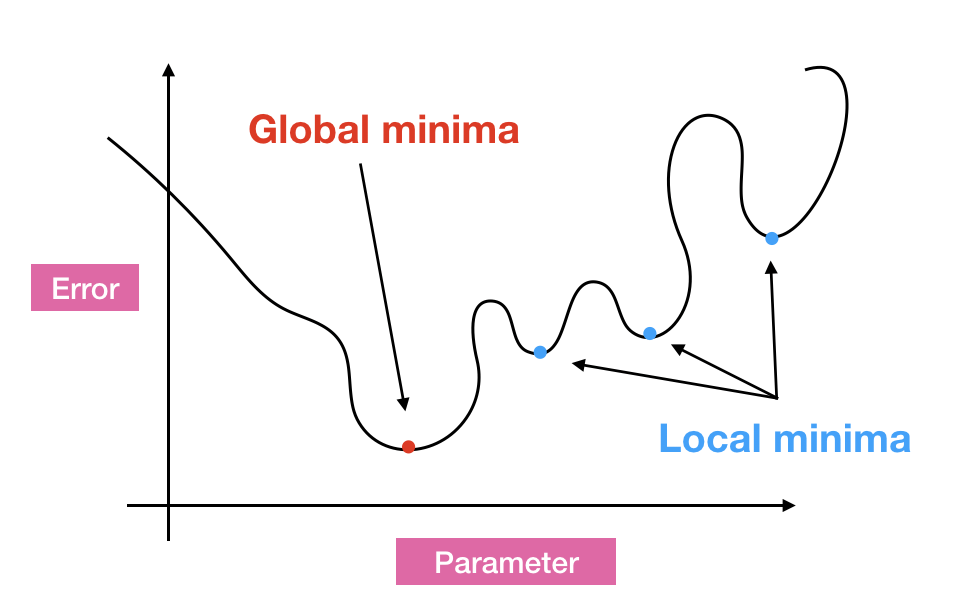
パラメータを動かして目的関数がもっとも小さくなる/大きくなるようにする。つまり、
目的関数が最小/最大になる時の解を見つけること
が学習になります。しかし、図を見てみると「local minimum (局所的最適解)」「global minimum (大域的最適解)」が混在していますね。青丸を変数の初期値としましょう。(学習を「どこ・なに」から始めるかを初期値という)そして学習(ただ下に向かうだけ)をさせると明らかに初期値によって異なるminimumに到達しますよね。これは機械学習における問題の一つなんです。僕も解決策は知りません。しかし、もし目的関数がお椀のような形をしていればどこからスタートしてもglobal minimumに行きますよね。そんな都合のいい目的関数の性質は「凸関数 (convex)」であることです。
関数![]() が凸関数であるとは
が凸関数であるとは![]() に対して(
に対して(![]() =任意)
=任意)
![]()
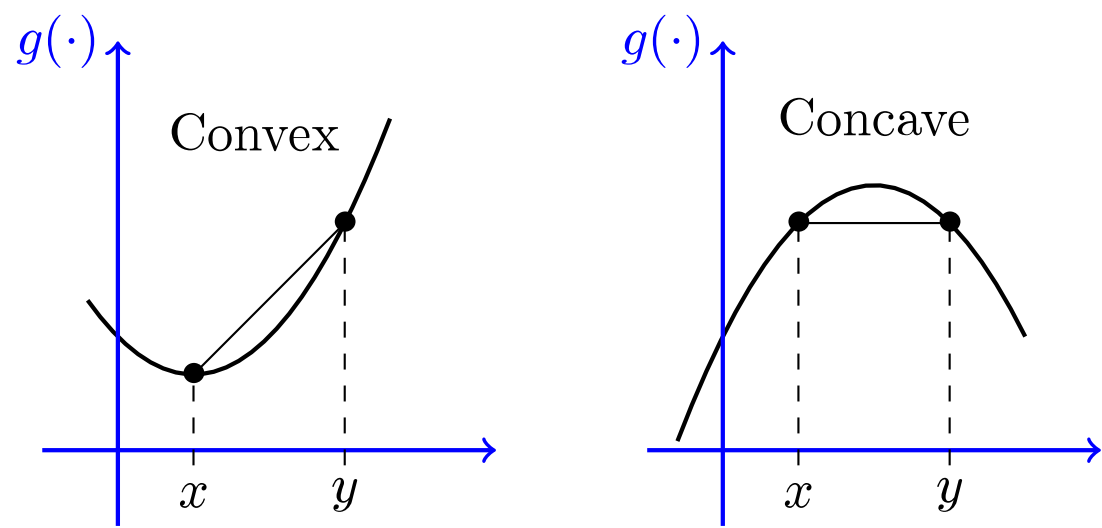
を満たす時に言う。また、凸関数についてはこれらがわかりやすいと思います。
- https://qiita.com/koshian2/items/90ac367089b5617519b2
- https://qiita.com/hiyoko9t/items/6742e7dc121cf4cbef09
- https://www.hellocybernetics.tech/entry/2017/01/16/011113#最適化問題の簡単な例
最後に等高線でのコスト関数を見てみましょう。基本的に多次元なので可視化はできませんが、等高線を用いた図は機械学習では頻出なのでぜひ見ておいてください。
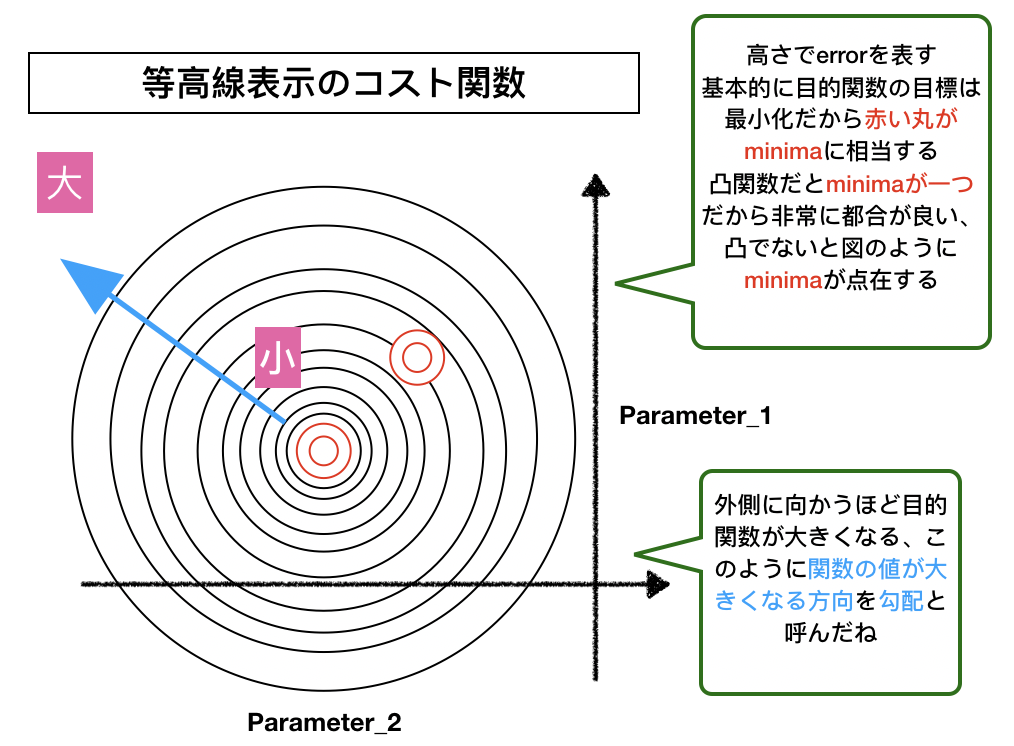
次回は「勾配法」についてお話しします。先走ると勾配法とはニュートン法に似ていて「ちょっとずつずらして最適解ゲットしようぜ」を行うものです。
でわ
README