本日からはニューラルネットワークweek。最新のものまで突っ走りましょう。
てゆーか、ニューラルネットワークってなんだったっけ?
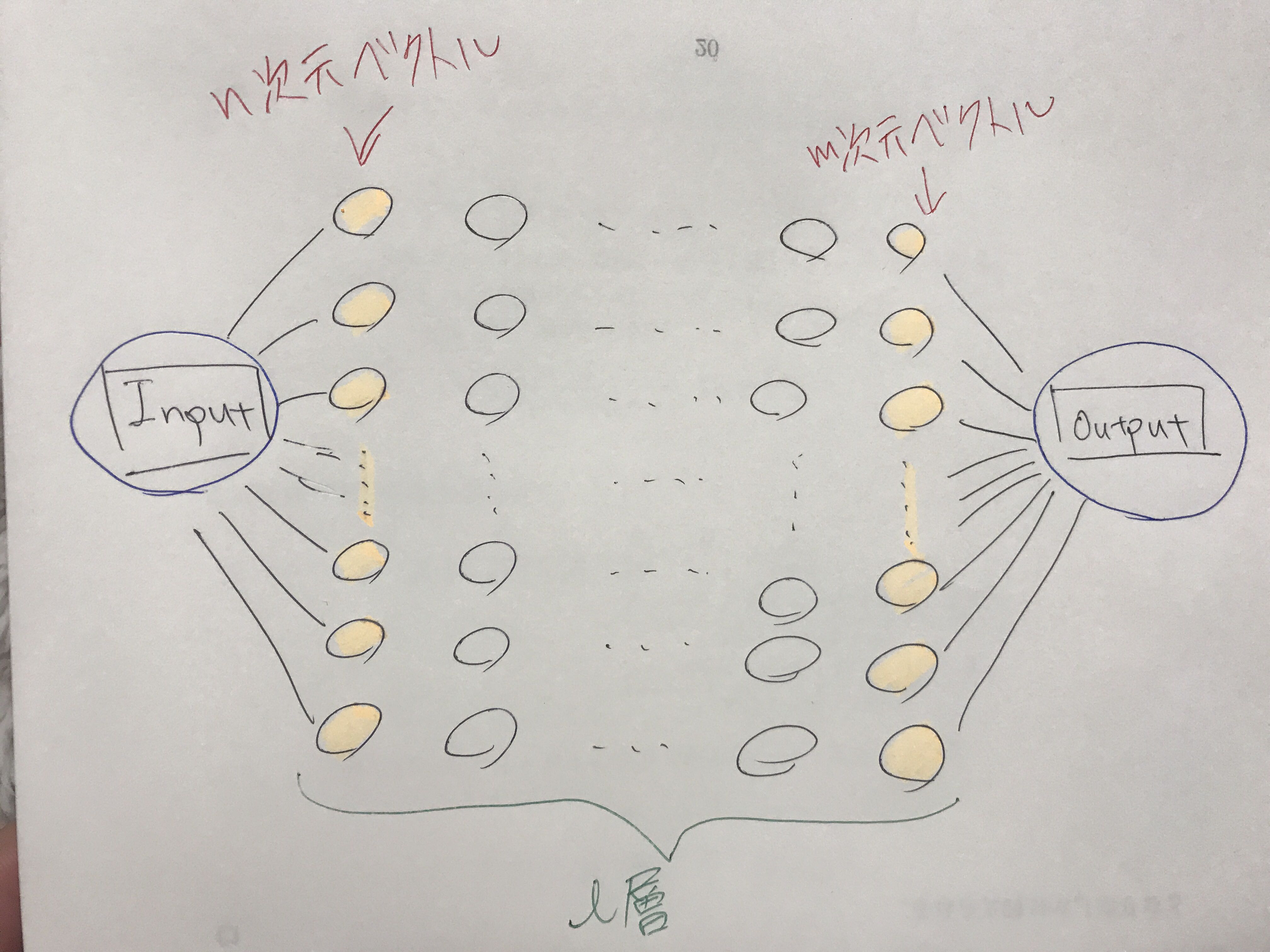
入出力数とか層数などは気にせずこんな風にニューロンを使った関数がニューラルネットワークでした。そして層が比較的深いものを多層パーセプトロンといいました。よく見ると
入出力がベクトル
になっていますね。いいんです。実際データなんてベクトル形式なんです。各学生のテストのデータも、競馬のデータも株価も終値とかを横並びにしてベクトルです。
しかーーし!

これ今日僕がとって虹なんですけど。こんな風に画像を入力としたい場合はベクトルじゃなくないですか?実際サイズは(691 × 502)ですし、しかもRGBなんです。RGBはレッド・グリーン・ブルーの略です、つまり3次元。
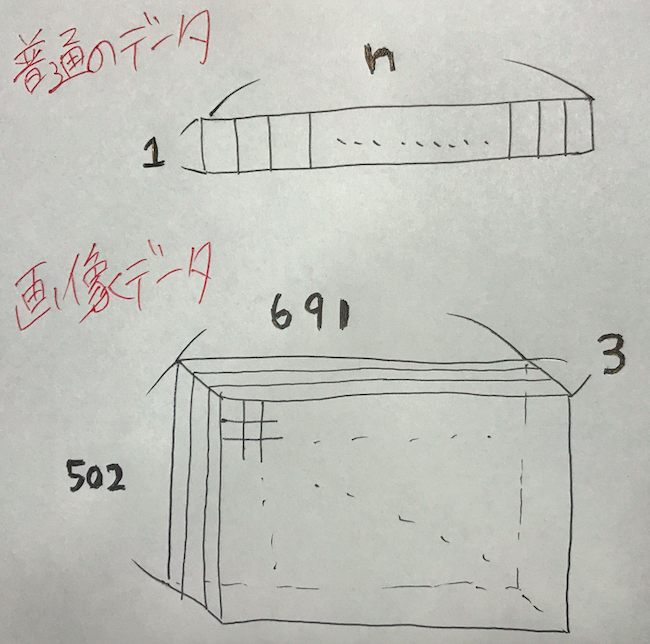
この画像のニューラルネットワークの入力として使いたいとするとこのままだと無理なので作戦を考える必要があります。
- とりあえずグレースケールにする(RGBからモノクロ)
こうするととりあえずデータのシェイプ(横,縦,奥)が![]() になります。しかしまだ行列のままなのでもう一工夫
になります。しかしまだ行列のままなのでもう一工夫
- 各行を横に並べて
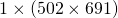 のベクトルにするもしくは縦に並べたベクトルにする
のベクトルにするもしくは縦に並べたベクトルにする
こうすることで画像をベクトルとして扱えるようになりました!わーい
それは無理やりすぎる
ごもっともです。行列をベクトルにするなんて邪道すぎますね。行列入力できるニューラルネットワークが
畳み込みニューラルネットワーク(Convolutional Neural Network)
なんです。そう、画像に特化したニューラルネットワーク。
けどどうやって行列入力可能にしたんや?
その前に、そもそもなんで画像をベクトルとして扱うべきでないかというと

たとえばこの画像、四角で囲ったところを1ピクセルだとします。ここだけ見ても何もわからなくないですか?というのはこのピクセルから学習できそうなことはあるのか?ということです。一方で
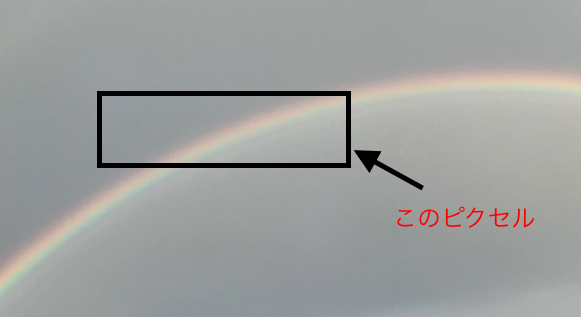
こう見るとどうですか?虹がハッキリと映っていてさっきよりは意味あるピクセルになっていますよね、つまり、コンピューターが画像を学習するには今までのようなベクトルの要素単位ではなくもっと大きな範囲を1単位として見る必要があるからです。それが
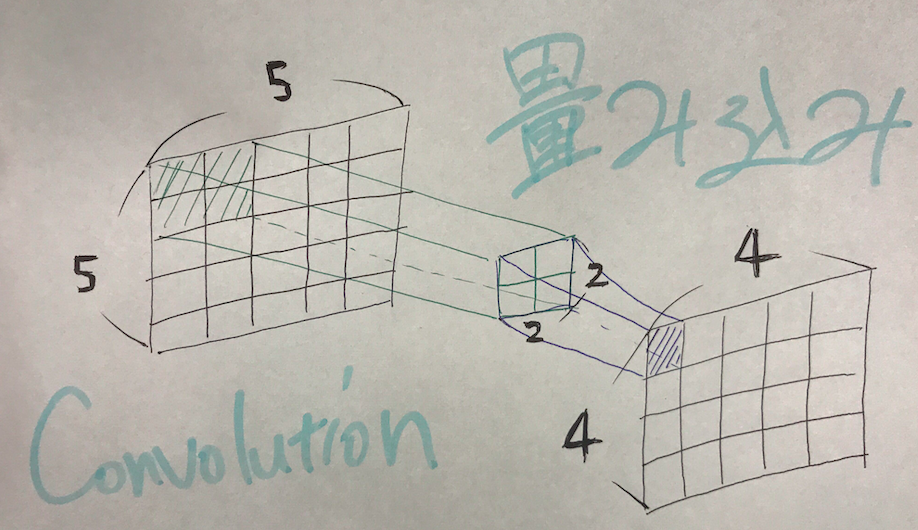
畳み込み
なんです。この場合だと真ん中の![]() 行列がコンピューターの目となりKernel matrixといったりします。これをずらしていって手前の出力を作るんですがとりあえず一気に定式化します。
行列がコンピューターの目となりKernel matrixといったりします。これをずらしていって手前の出力を作るんですがとりあえず一気に定式化します。
- 入力シェイプは
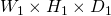
フィルタ数: K
フィルタサイズ: F
スライド幅: S
パディング: P - 出力シェイプは
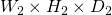
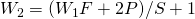
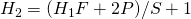
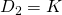
フィルタサイズとはKernelサイズのこと、スライド幅はフィルタのずらし幅、パディングは画像の縁に新たなピクセルを組み込むことzero-paddingがメジャー。これは縁に0ピクセルを付け加えること、こうすることで
- 縁の畳み込み回数が増える
- パラメータの更新数が増える
- カーネルのサイズを調節できる
などのメリットがあります。
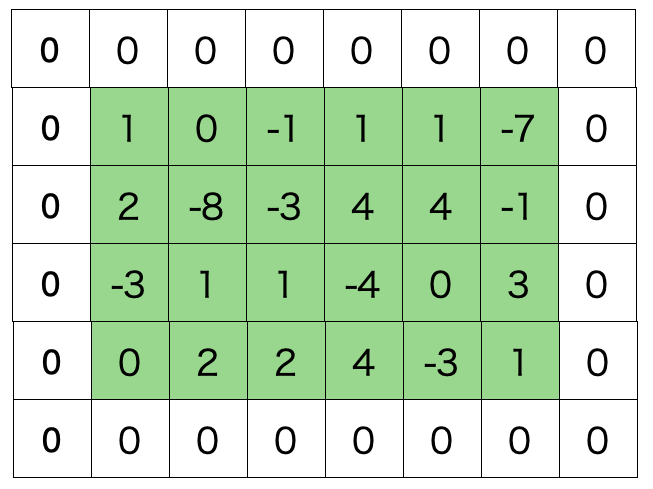
そして出力のシェイプで分母に![]() とありますがこれについては次の図を見てください。緑が入力、オレンジが出力
とありますがこれについては次の図を見てください。緑が入力、オレンジが出力
スライド幅: 1
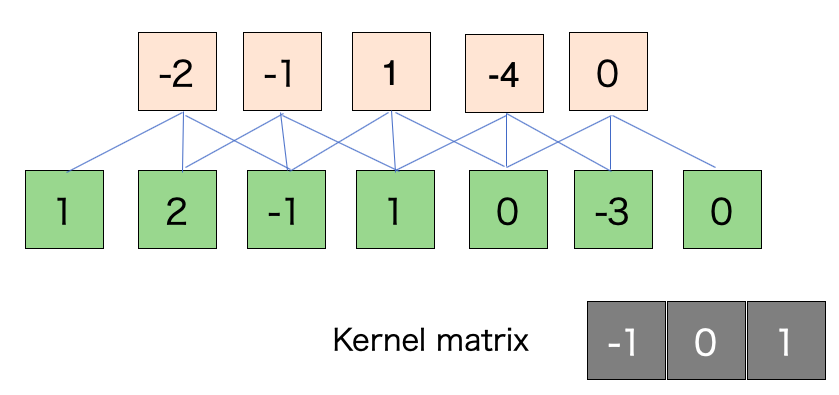
スライド幅: 2
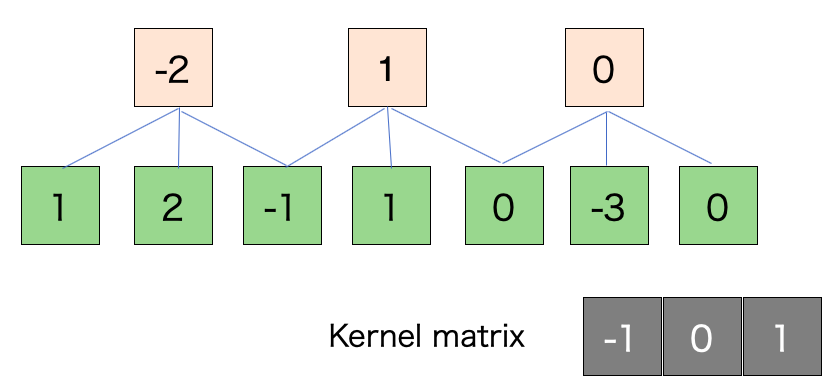
緑のブロックにカーネルを重ね合わせ線型結合を計算します。この際、スライド幅が適切でないシェイプが少数になるのでそこだけ注意。
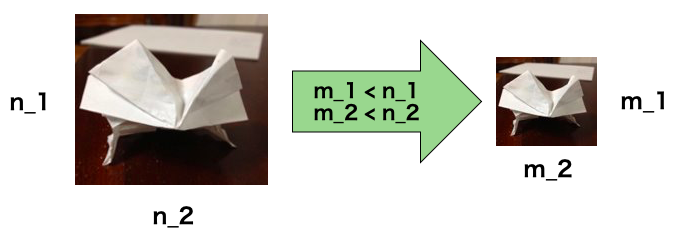
CNNでは畳み込みに加えてPoolingという操作があります。これは画像の縮小です。今までのニューラルネットワークでは隠れ層のノード数を減らすことで次元を落としていました。これを行列入力においても可能にしようというものです。
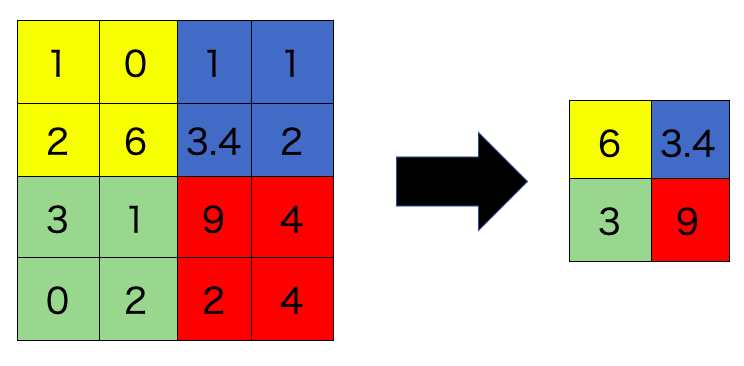
具体的な方法はMax-poolingというものです。![]() のKernelでスライド幅2だと次のようになります。
のKernelでスライド幅2だと次のようになります。
定式化すると
- 入力:
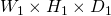
フィルタサイズ: F
スライド幅: S - 出力:
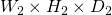
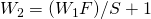
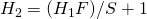
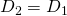
となります。しかし、Poolingという操作はあまり人気がないらしいのでスライド幅の大きい畳み込みで対処するようです。
最後に次のリンクが非常に参考になるので見てみてください。
本日はここまでです。でわ。