こんにちは。理論編で主成分分析についてはみなさん理解できたと思います。が。本日は少し応用です。
とりあえず復習から始めましょう。
PCAは固有ベクトルへの射影
そうです。たとえば400次元から2次元へのPCAは固有値を大きい方から2つ選び、対応する固有ベクトルに射影です。つまり
軸を新しく定義している
つまり
空間が変わっている
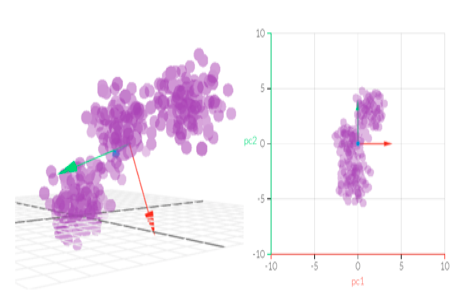
まさにこの図、3次元のデータ(左)にPCAをかけて2次元データ(右)にしている。軸が異なるどころかその数も変わっていることより空間が変わったことは明らか。
しかし、今回は
次元を保ったまま空間を押しつぶす
をします。
重要なのは次の考え方のみ!
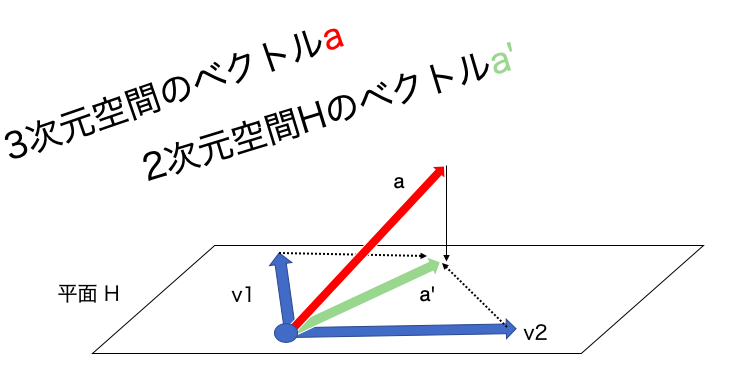
適当に作った例だと
![]()
が前回のPCAに対し
![]()
のように次元を保ったまま平面上の点に置き換える。上の図だと![]() に対し
に対し
![Rendered by QuickLaTeX.com \[ a' = c_1v_1 + c_2 v_2 = c_1 \begin{pmatrix} v_{11} \\ v_{12} \\ v_{13} \end{pmatrix} + c_2 \begin{pmatrix} v_{21} \\ v_{22} \\ v_{23} \end{pmatrix} \]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-74f974780f6b5ea2d2521d4080520c37_l3.png)
とできる。ただし、![]() である。
である。
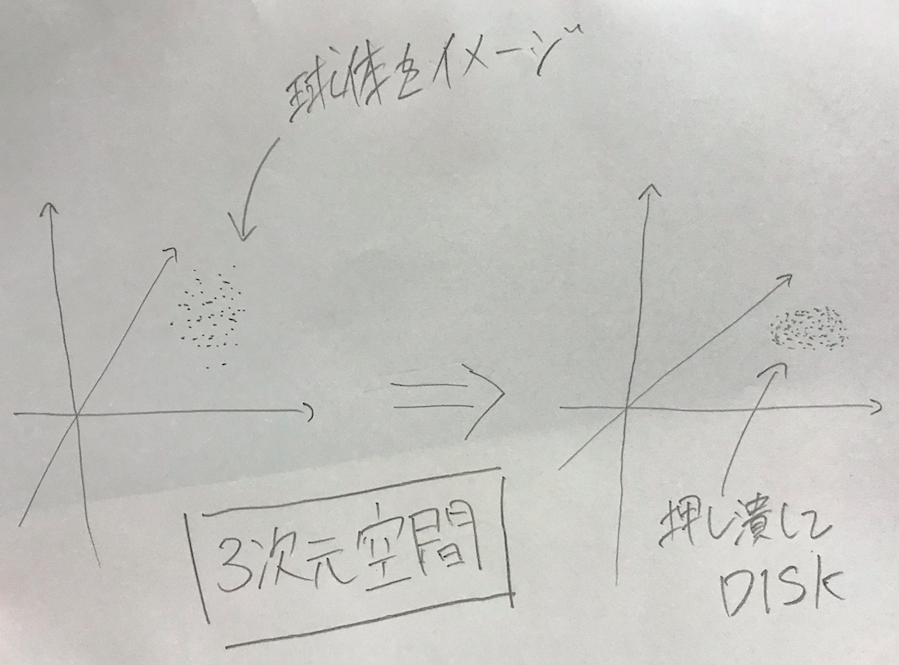
まとめると、
あるベクトルたちの線型結合で全部書き直そう
ということ。上では3次元ベクトル2本![]() 用いて平面を構成した。
用いて平面を構成した。![]() を平面H上の点
を平面H上の点![]() としようということ、これを全データ点で行う。計算してみよう。
としようということ、これを全データ点で行う。計算してみよう。![]() とすると
とすると![]() で
で![]() が貼る平面状の点を表すことができるので
が貼る平面状の点を表すことができるので
![]()
を最小化するような![]() を見つければいい。このとき
を見つければいい。このとき![]() となる。ここで
となる。ここで
![]()
![]()
これらの公式を用いて
(1) 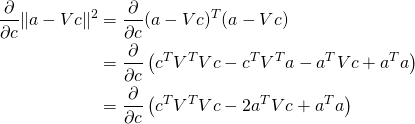
微分を0とする。
(2) 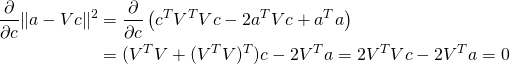
従って逆行列をかけることで
(3) ![]()
つまり!
(4) ![]()
が![]() である。
である。
![]()
を
Vの列ベクトル空間がはる空間への射影行列
という。
では数学の時間です。
データ![]() (m次元)
(m次元)
平面を貼るベクトルを![]()
ただし![]() ,
, ![]()
とする。目標は![]() を見つけ出すこと。見つかれば上で導出した射影行列を全データにかければ良い。なんだけど、ちょっと長くなるから次の記事で。
を見つけ出すこと。見つかれば上で導出した射影行列を全データにかければ良い。なんだけど、ちょっと長くなるから次の記事で。
でわ。
READMORE