こんにちは。
本日はprior distributionについて深入りしてみようと思います。事前分布って不思議ですよね。個人的には共役事前分布って誰が見つけたのかなー?と永遠思ってます。事前分布のスキルを高めるということはベイズの力を高めるということだと思います。なのでやっていきましょう。
Conjugate Prior
欲しいものはいつもposterior distributionです。
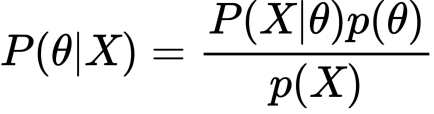
![]() と
と![]() が同じ分布になる時、そのpriorをconjugate priorといいます。共役事前分布です。しかし、実世界においてconjugate priorで十分か、といいますとそうではありません。なので現状はMCMCを使った次のようなアルゴリズムを使って数値計算するらしいです。
が同じ分布になる時、そのpriorをconjugate priorといいます。共役事前分布です。しかし、実世界においてconjugate priorで十分か、といいますとそうではありません。なので現状はMCMCを使った次のようなアルゴリズムを使って数値計算するらしいです。
- Stan
- WinBUGS(Bayesian inference Using Gibbs Sampling)
- OpenBUGS(Bayesian inference Using Gibbs Sampling)
- JAGS(Just Another Gibbs Sampler)
- PyMC(Hamiltonian Monte Carlo)
- INLA(Integrated nested Laplace approximation)
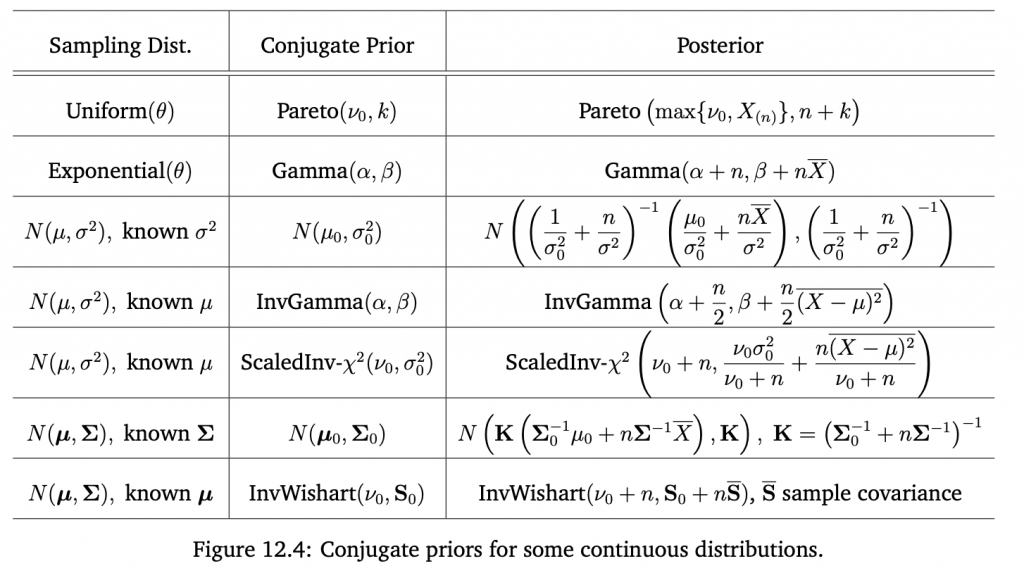
とはいえ共役事前分布はもう皆さんご存知で、飽きていると思うので少し特殊なPriorを見ていこうと思います。
Improper Prior
事前分布が以下を満たす時、improper priorと言います。
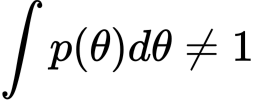
たとえば、
などです。priorがimproperであることが問題かどうかは人によってことなるようです。ベイジアンのLuca Rossiniという方はimproperでも問題ないと言っているようです。とはいえ、ベイズの定理の右辺が求まらないのであれば事後分布を得ることはできないのでもともこもありません。
Uninformative Prior
とはいえパラメータの事前分布なんてわからないのにどうすればいいんだ、、、という時に使われるのが無情報事前分布です。non-informative priorともいいます。情報がない、以外にも次の理由で使われたりします。
- priorの事前情報がない
- posteriorに変な影響を与えたくない
- データのみの情報でposteriorを決定したい
一様分布はいい例じゃないでしょうか。そして他には以下のようなものがあります。

ここではJeffry’s Priorについて深入りしようと思います。
Jeffrey’s Prior
以下を満たす時、パラメータ![]() のpriorが近似的にnon informative priorとなり(次で話します)、そのpriorをJeffreyの事前分布といいます。
のpriorが近似的にnon informative priorとなり(次で話します)、そのpriorをJeffreyの事前分布といいます。
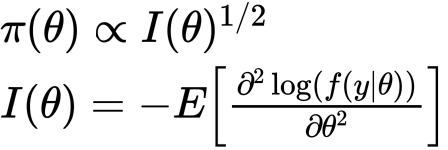
見ての通り、フィッシャー情報量のルートになっています。また、このpriorはリパラメタライゼーションに対して不変です。これについては下で述べます。
とはいえ、これだけだとなにを意味してしているかよくわかりません。なので簡単な例、二項分布でJeffrey priorを求めてみます。
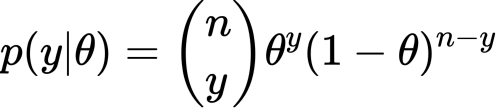
尤度は上のものを考えます。Jeffrey priorを![]() と表すことにします。
と表すことにします。
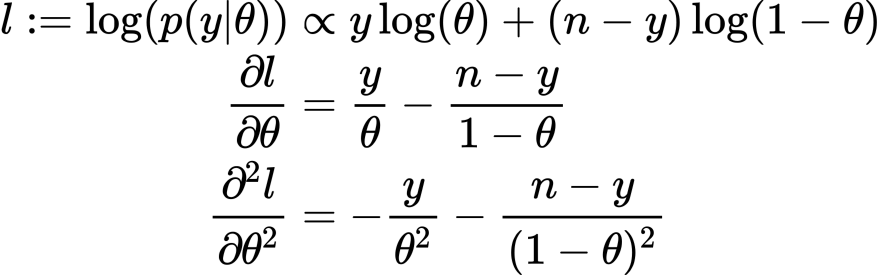
よってフィッシャー情報量は
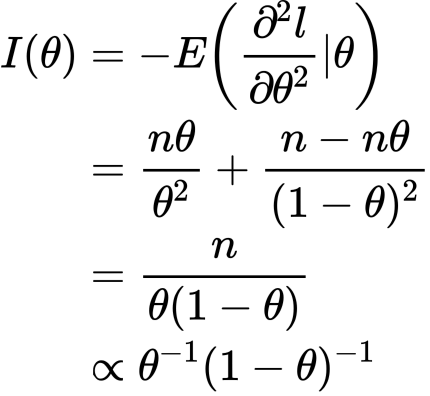
したがって
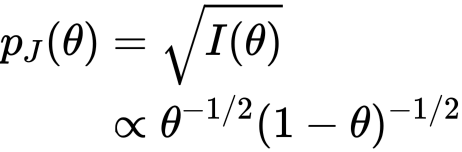
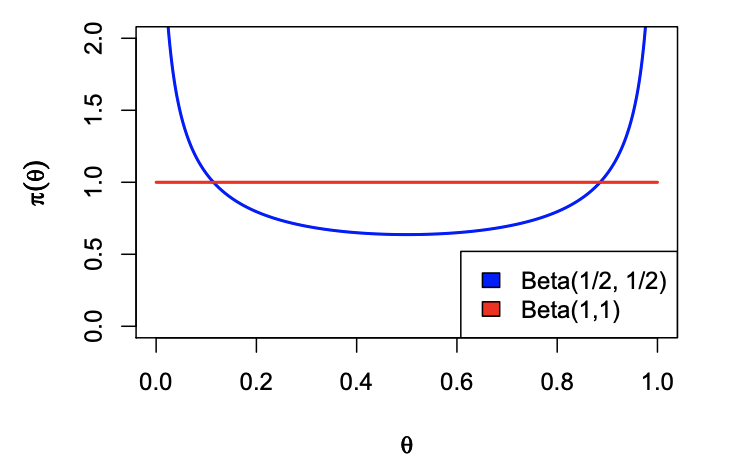
とこの尤度に対するJeffrey priorを求めることができました。しかもよく見るとこれは![]() ですね。ついてでに分布も見ておきます。
ですね。ついてでに分布も見ておきます。
ちなみにリパラメタライゼーションについては全単射な関数![]() を考えます。このとき
を考えます。このとき![]() という変数変換にたいして
という変数変換にたいして![]() は次の二通りの方法で得られます。
は次の二通りの方法で得られます。
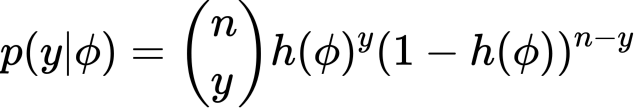
まずは変数変換後の尤度を用いて計算する方法。そして
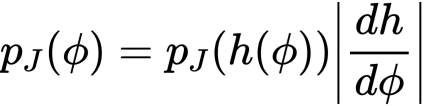
ヤコビを使う方法です。たとえば
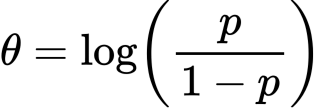
というリパラメタライゼーションを考える例は参考文献にあるので気になる方はどうぞ。
Jeffrey’s Priorの意味
さて、これを使う意味ですが個人的には2つあると思っています。
- リパラメタライゼーションによる新しいモデル構築が容易な点
- posteriorとのKLを最大ができる点
まず、一つ目は対象のパラメータに対して別のモデルを考える時にヤコビをかけるだけで済むのがいい点の一つだと思います。
そして二つ目、こちらが各だと思っています。Jeffreyを用いることでそのposteriorとのKLを最大化させることができます(データが十分多い時)。これによってposteriorはpriorには極力影響されない一方で、最大限にデータの影響のみを受けた分布になります。つまり、データをはっきりと表現していることになります。

実はこの話はBernardo reference priorというものと関係があるようです。そのパラメータ![]() が一変数という条件がJeffrey Priorと一致するようです。
が一変数という条件がJeffrey Priorと一致するようです。
こういう意味でJeffrey priorはuninformativeと言われているようです。ついでにパラメータをいじった事後分布の結果を見てみましょう。
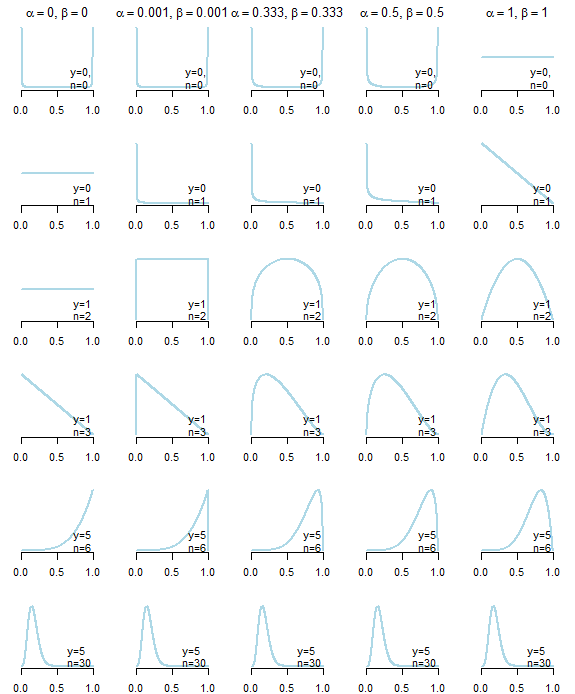
5種類の事前分布に対する事後分布の変化の図です。Jeffrey Priorは右から二つ目です。データの情報を最大限に説明する分布と言いましたが、まさにそうなんじゃないかなと思いました。まず注目すべきは![]() です。一回の試行で裏の出た時ですが、パラメータはグイっと左によっています。右の一様分布ではそうなりません。
です。一回の試行で裏の出た時ですが、パラメータはグイっと左によっています。右の一様分布ではそうなりません。
次に注目したのが![]() です。
です。![]() の同じ条件と比べると事後分布が綺麗に半円を描いています。関数が滑らかであることはいろいろと都合がいいと思うのでこれもJeffreyの良さかなと思いました。
の同じ条件と比べると事後分布が綺麗に半円を描いています。関数が滑らかであることはいろいろと都合がいいと思うのでこれもJeffreyの良さかなと思いました。
お気づきかと思いますが、![]() と比べるとあまり差がないように思います。僕もそう思いもう少し調べてみました。
と比べるとあまり差がないように思います。僕もそう思いもう少し調べてみました。

見ての通り、事後分布にそれほど大きな差はないと思いました。よって僕の中の結論としてはデータ数が非常に少ない場合においてJeffrey Priorは力を発揮するのでは?です。
僕的まとめ
この記事でreference priorとjeffrey priorの二つの新しい事前分布を紹介しましたが、共役に加えて最終的なベストなものは何なのか、というのが気になる点です。パラメータについて考慮するものがなければ共役事前分布またはreference priorがいいなと思いました。ここで、考慮するものとはたとえばデータのタイプであったり、物理的な何かであったり詳しいことは僕にはわかりませんが事前情報というよりは制約的な形で考慮するものなんだと思います。たとえば、画像処理における事前分布だと以下のようなものがあります。
そしてこのJeffrey Priorですが改めてまとめますと、これベルナドのrerefence priorの単変量バージョンに相当します。そしてこれはフィッシャー情報量から導出されます。これはつまり今あるデータから事前分布を構築するということを意味します。したがってよく使われる直感、inductive biasというべきでしょうか、の影響を極限まで希薄した事前分布を意味します。また、無情報事前分布と言われている理由はデータが十分に大きい場合、事後分布とのKLを最大化させるためです。この証明は参考文献にあります。最終的には場合分けで解が得られていました。
話が長くなりましたが今回個人的には学ぶことが多かったです。情報幾何に少し近づけた気がします。でわ
References
- https://stats.stackexchange.com/questions/58564/help-me-understand-bayesian-prior-and-posterior-distributions
- https://stats.stackexchange.com/questions/78606/how-to-choose-prior-in-bayesian-parameter-estimation
- http://www.stats.org.uk/priors/noninformative/YangBerger1998.pdf
- https://stats.stackexchange.com/questions/87321/does-the-bayesian-posterior-need-to-be-a-proper-distribution
- https://www.johndcook.com/CompendiumOfConjugatePriors.pdf
- https://stats.stackexchange.com/questions/283703/difference-between-non-informative-and-improper-priors
- https://www.slideshare.net/hoxo_m/ss-59418886
- https://zhenkewu.com/assets/pdfs/slides/teaching/2016/biostat830/lecture_notes/Lecture14.pdf
- http://www.stat.cmu.edu/~larry/=sml/Bayes.pdf
- https://stats.stackexchange.com/questions/297901/choosing-between-uninformative-beta-priors/
- https://www4.stat.ncsu.edu/~wilson/bayes/noninformative_priors3.pdf
- https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/lectures/lecture7.pdf
- https://stats.stackexchange.com/questions/7519/why-are-jeffreys-priors-considered-noninformative/39098
- https://www2.stat.duke.edu/courses/Spring13/sta732.01/priors.pdf
- https://www.zhihu.com/question/67846877