こんにちは。
本日は機械学習のモデルの評価方法についてまとめます。Gistsがかなり重くなってしまったので一発で見れない場合はColabで開くか、Gistsに飛んだのちページを何度か更新してみてください。
分類指標
この記事では分類問題に焦点を当てます。なので回帰におけるMSEとかは話しません。
- TP / TN / FP / FN (真陽性 / 真陰性 / 偽陽性 / 偽陰性)
- confusion matrix (混同行列)
- simple accuracy (正解率)
- recall (再現率) (sensitivity)
- precision (適合率)
- f1 measure (F値)
- f1 beta measure (重み付きF値)
- threshold (閾値)
- ROC / AUC (受信者操作特性 / AUC下部の面積)
- MCC (マシューズ相関係数)
これらのベーシックな指標についてまとめます。またF-betaについては少し深入りします。でわやっていきましょう。
分類指標の必要性
もちろん、汎用性がめちゃくちゃ高いものがあればそれでいいんですが残念ながら私は知らないです。。。他にも具体例で考えてみましょう。
たとえば、100枚のラーメンの写真をデータセットとします。モデル![]() で
で
- 二郎系だ
- 二郎系ではない
という分類をしたとするじゃないですか、Accuracy=99%となったとするじゃないですか、この数値だけ見ればすごく上出来なんですけど仮に100枚中1枚しか二郎系がなかったとしたら![]() はなにも考えず1を出力するだけで99%とれちゃいますよね。これって
はなにも考えず1を出力するだけで99%とれちゃいますよね。これって![]() はまともな学習をしていないことになりますよね。つまり、このモデル
はまともな学習をしていないことになりますよね。つまり、このモデル![]() よくないですよね。
よくないですよね。
Confusion Matrix
クラス分類の結果をまとめた表のこと。各要素がTP / TN / FP / FNとなる。ただし、これは二値の場合。しかし多値分類でも同様に作れます。
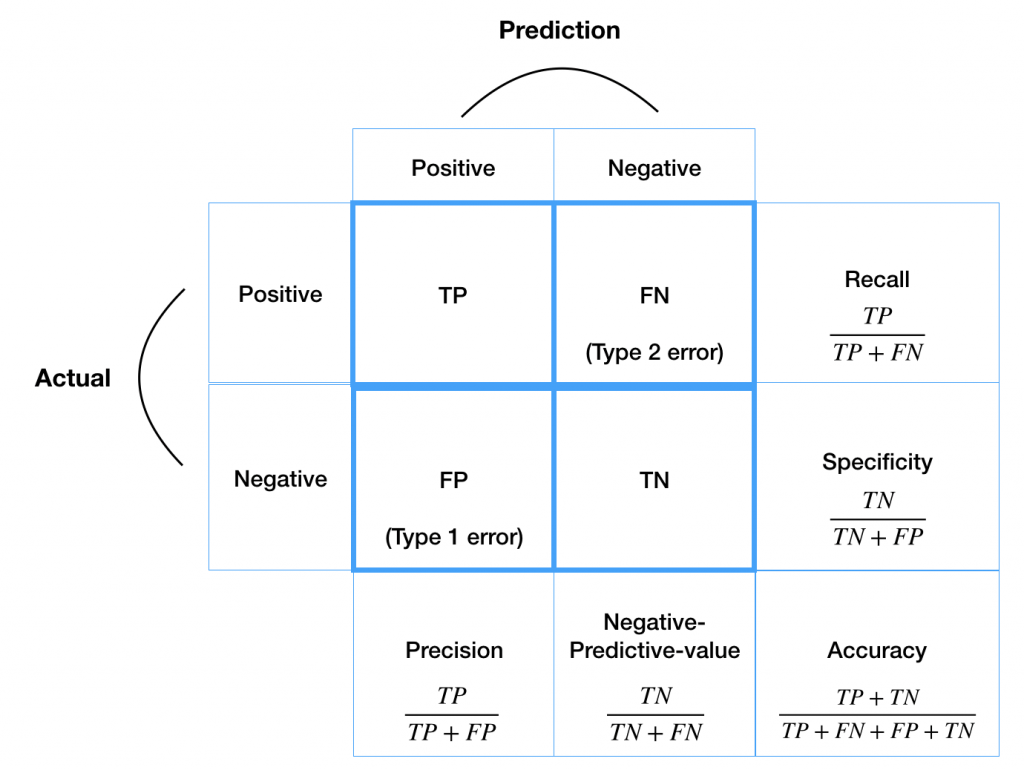
Pythonで実装する際はパーセンテージも表示させるといいですね。
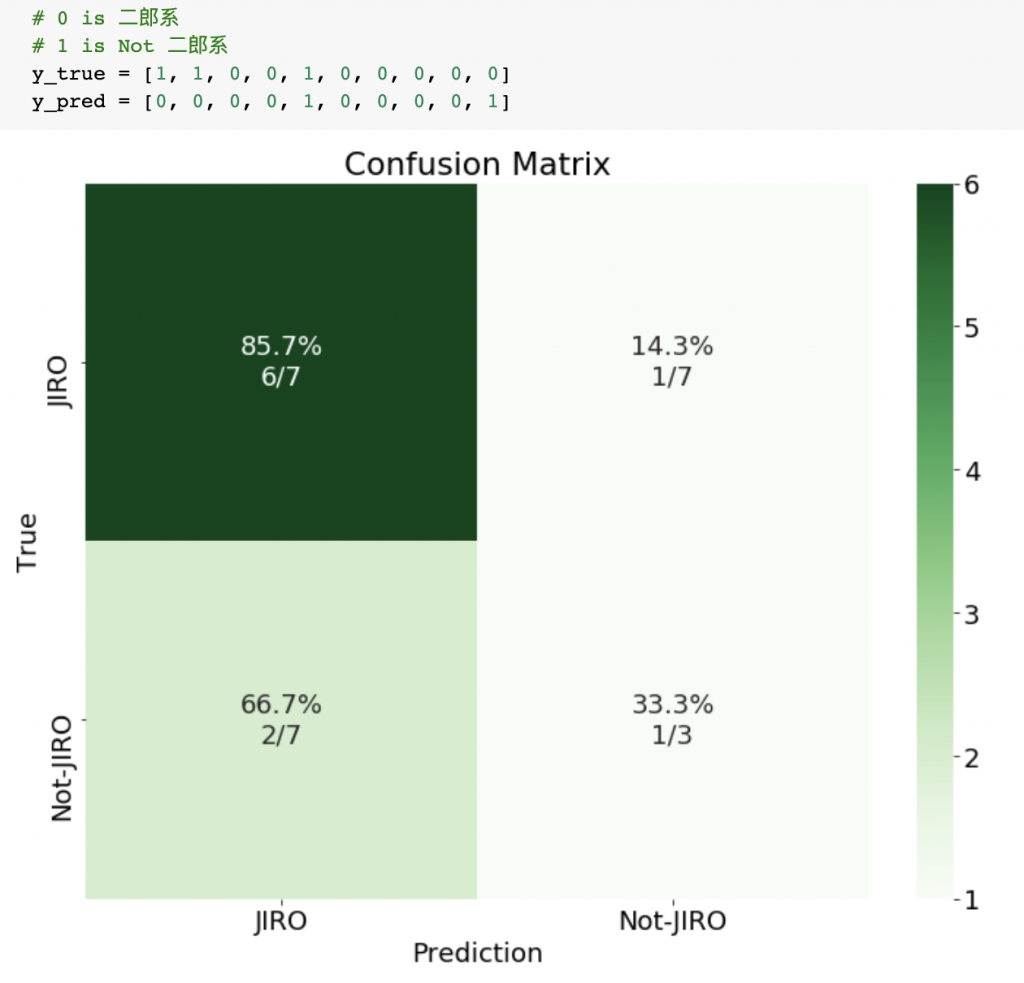
で、Confusion Matrixの中の指標を一個づつ見ていきます。
Accuracy
もっとも、シンプルかつ、直感的な正答率
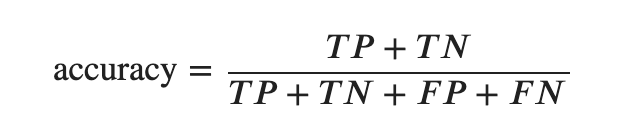
Precision
少しの外れを許すが機会損失したくない時に使う
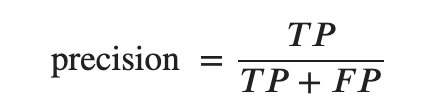
Recall (Sensitivity)
機会損失してでもとにかく正確に当てたい時に使う
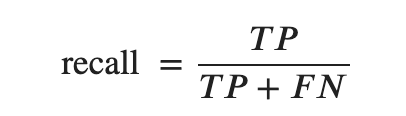
PrecisionとRecallの具体例
たとえば全国の二郎系を制覇したいという目的に対してはRecallよりもPrecisionを重視します。なぜならば行ったラーメン店が高い確率で二郎系あっても素通りしてしまっては目標が達成できないからです。
逆にRecallを重視するのはたとえば病気を判別するときです。病気なのに病気ではない、と判断すると大変ですよね
とはいえ、完璧な分類は共に高いのでどうせならこの二つの指標を同時に見たいですよね。つまり。2つの指標を同時に加味して「全体としての良さ」を測りたい時に![]() の登場です。
の登場です。
F1 measure
RecallとPrecisionを同時に考慮する指標です。調和平均という見方もできますが![]() が「外れの総数」であることに注意すると外れの平均を考慮した正解率と考えることができます。
が「外れの総数」であることに注意すると外れの平均を考慮した正解率と考えることができます。
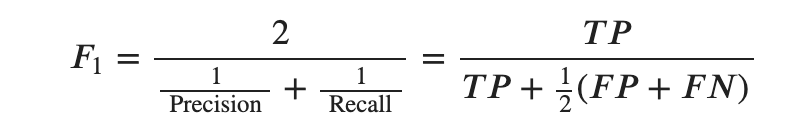
しかしです。先程の例のようにどっちかを特別重要視してモデルを評価したい時多いですよね。つまり、recallとprecisionを同じくらい重視して全体の良さを図るのではなくどちらかを相対的に重視したモデルの良さの指標が欲しい時の方がぼくは多い気がします、そこで![]() の登場です。
の登場です。
F-beta measure
RecallとPrecisionに重みを加えたF measureです。いわば一般化です。
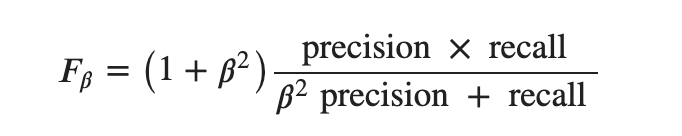
Precisionを重視したいなら (![]() )
)
![]()
Recallを重視したいなら (
![]()
しかしです、この式おかしいと思いませんか?相対的に重みづけするならば一方が![]() でもう片方は
でもう片方は![]() だと思いませんか?つまり
だと思いませんか?つまり
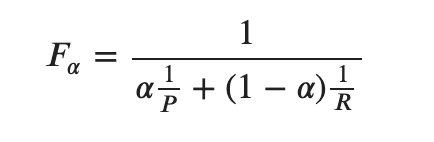
のほうが自然なF-betaですよね?え?ぼくだけ、、?笑。まあそういうことにしてちょっと聞いてください。
van Rijsbergen’s E (effectiveness) function
F-measureは実は別の指標から導出されたものらしいです。起源は次のもの
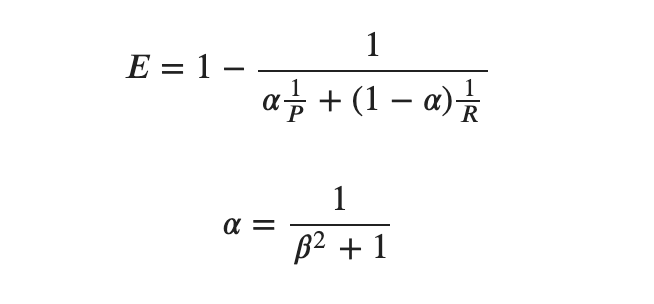
前述の![]() の定義が[Chinchor, 1992]なのに対してこれは[van Rijsbergen, 1979]です。たしかに古い。
の定義が[Chinchor, 1992]なのに対してこれは[van Rijsbergen, 1979]です。たしかに古い。
代入して変形します。
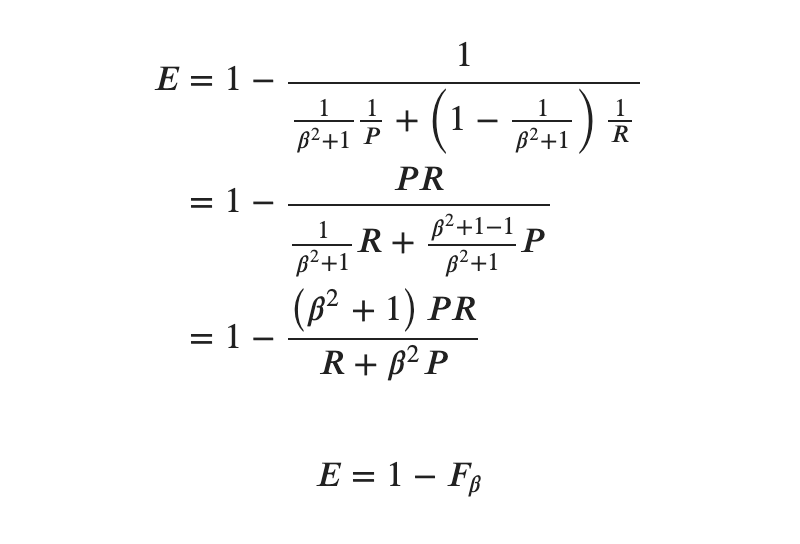
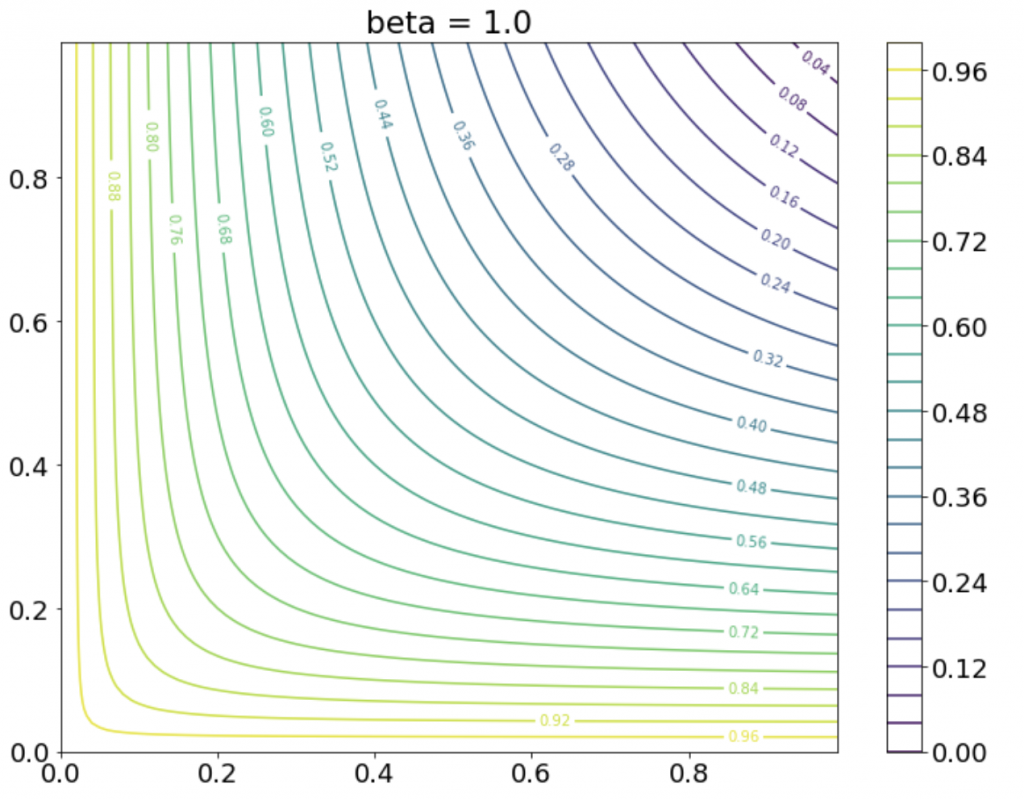
この関数![]() を
を![]() でプロットしてみます。
でプロットしてみます。
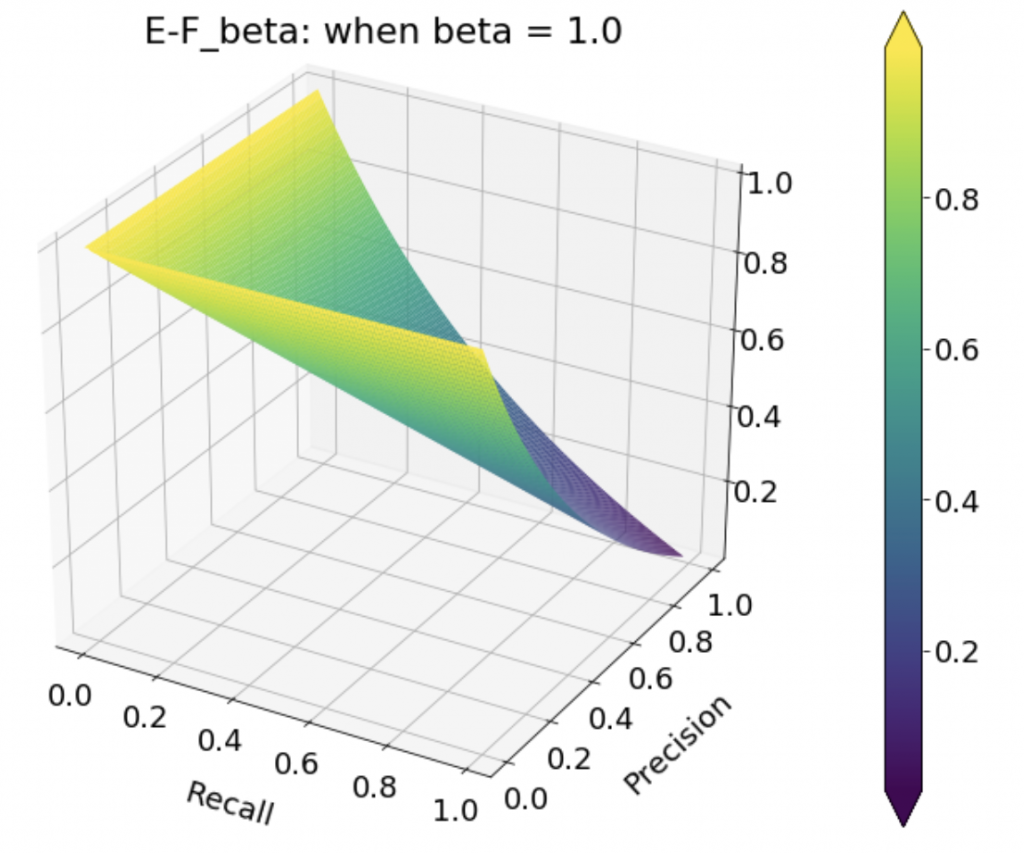
次は![]() を動かしていって
を動かしていって![]() を見てみます。
を見てみます。![]() ではないことに注意。
ではないことに注意。
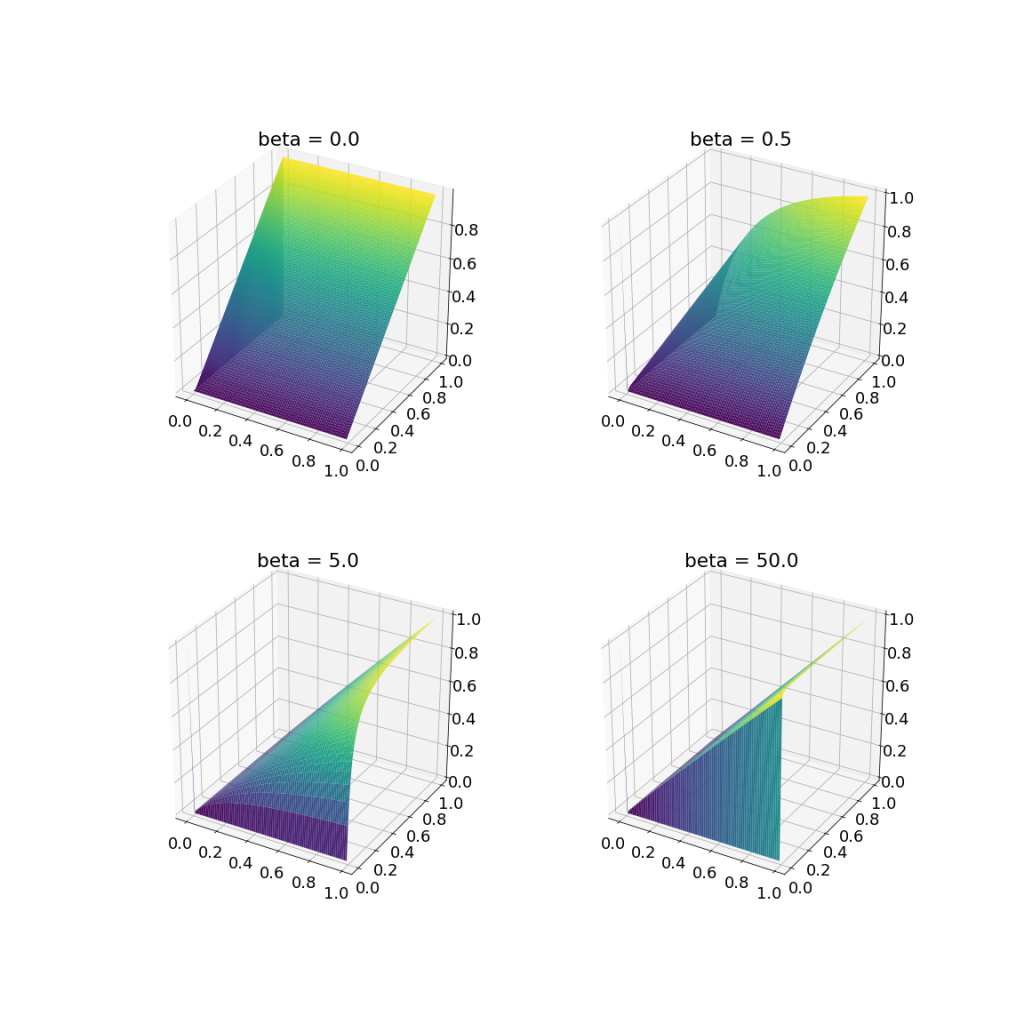
で、このグラフを頭に置いたまま話を戻すと関数![]() の
の![]() はなぜあのような形なのか?気になります。調べますと次の条件を満たすようにされているらしいです。
はなぜあのような形なのか?気になります。調べますと次の条件を満たすようにされているらしいです。

真実を確かめるために計算していきます。
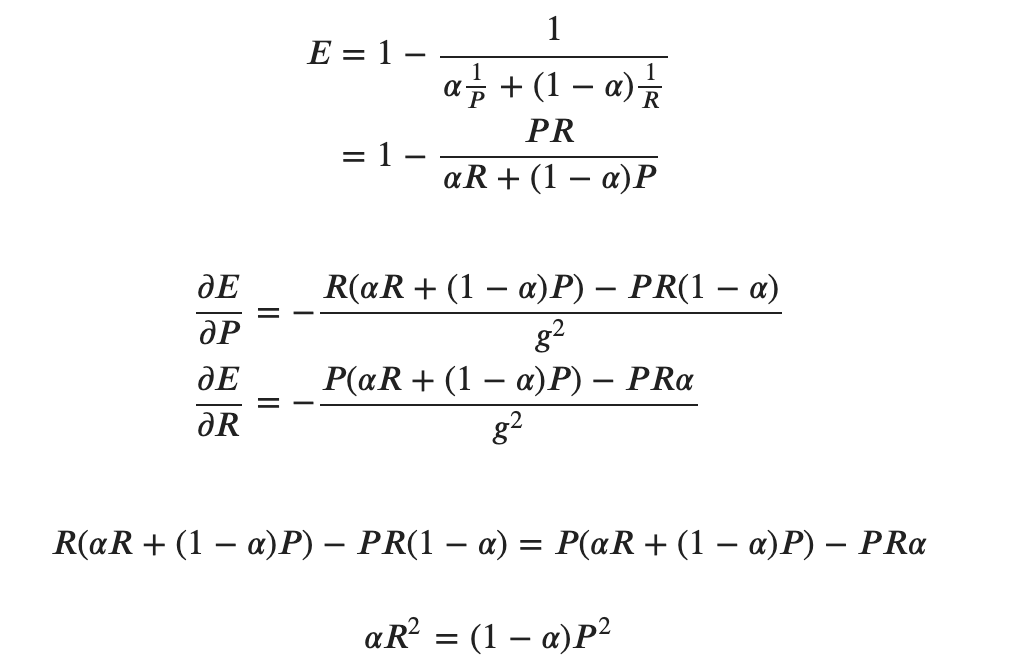
ここで ![]() なので
なので ![]() を
を ![]() と置き換えて
と置き換えて
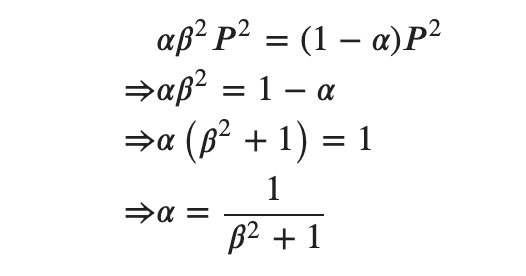
と、確かに導出されました。しかし、勾配が等しくなるという条件にどういう意味があり、なぜ必要なのかは理解できませんでした。すいません、、
とはいえ、わかったことをまとめると直感的な加重調和平均は![]() の方だということ。重み
の方だということ。重み![]() に戻して考えると
に戻して考えると![]() が
が![]() のとき重みが1/3対2/3になり、たしかに直感的に2倍の重みを置いていることになりますね。
のとき重みが1/3対2/3になり、たしかに直感的に2倍の重みを置いていることになりますね。
ROCとAUC
確率出力に対して最もいい閾値を見つけると同時に、モデルを比較するための指標をグラフ化したものです。
グラフ上の点は特定の閾値を用いてラベリングされたのちの混合行列から算出されたspecificity, sensitivityである。次の動画がかなりわかりやすいので絶対見てください。
簡単にまとめると、例えばロジスティック回帰を用いた2値分類を考えます。この時に閾値をいくつにするかが問題ですよね。出力の確率と閾値を比較して大きければ1,小さければ0のようにラベルを振る必要があるからです。つまり実数からカテゴリカルに変換する必要性。
ということはです、もちろん閾値と混合行列は一対一対応します。
どの閾値がもっともいい分類をしてくれるのか?という問に答えてくれるのがROCです。
そしていくつかのモデルに対してどのモデルがいいか、つまりどのROCがいいかという問に答えてくれるのがAUCです。
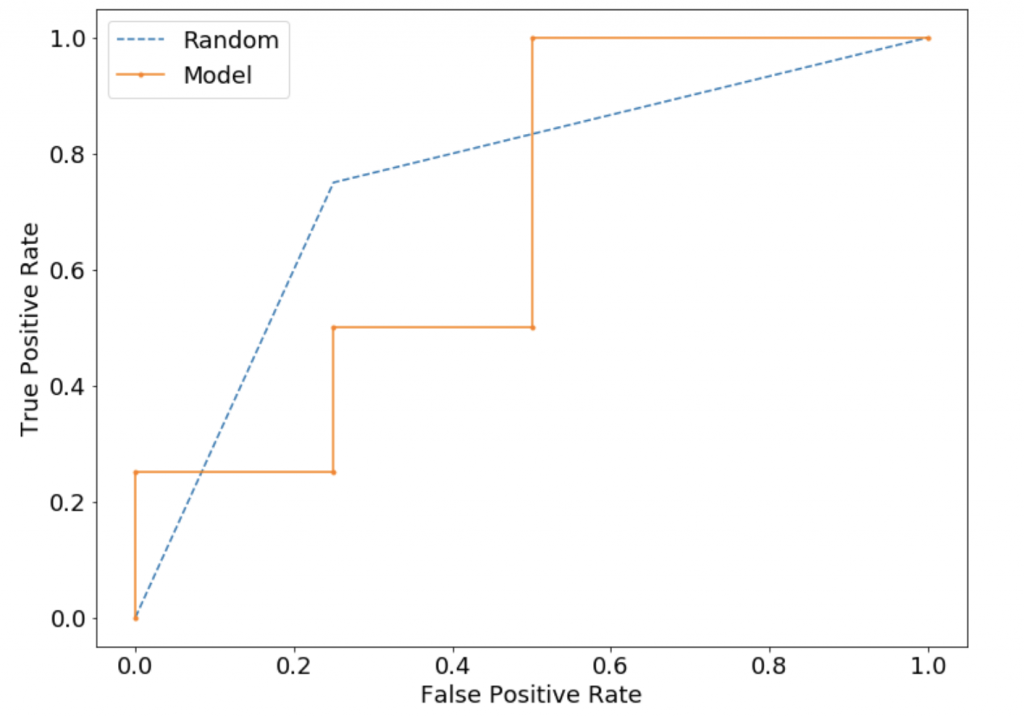
各軸はTPR、FPRとよばれます。言い換えると縦がRecallで横が(1-Sepecificity)です。つまり左上に近づくほど理想的であることがこの定義よりわかります。
そして上の図中の点ですが、これひとつひとつが特定の閾値によって算出された混合行列を用いて計算されたTPR、FPRです。
ここでわかったこととして他クラスのROCはそう単純ではないということです。sklearnに実装はありますがバイナリ で実装されているのか閾値をクラス数で分割しているのかわかりませんが、理論上はそう簡単にROCが作れないことは気にかけておいた方がいいと思います。
MCC
各クラスのサイズが非常に異なっていても使用できる評価指標です。
この記事の冒頭で極端な例をあげましたが、実世界の分析においてはよくあることだと思います。ですのでその点ではいい指標だなと思います。
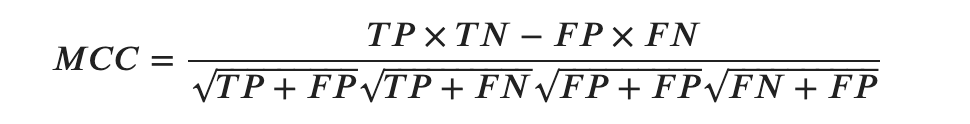
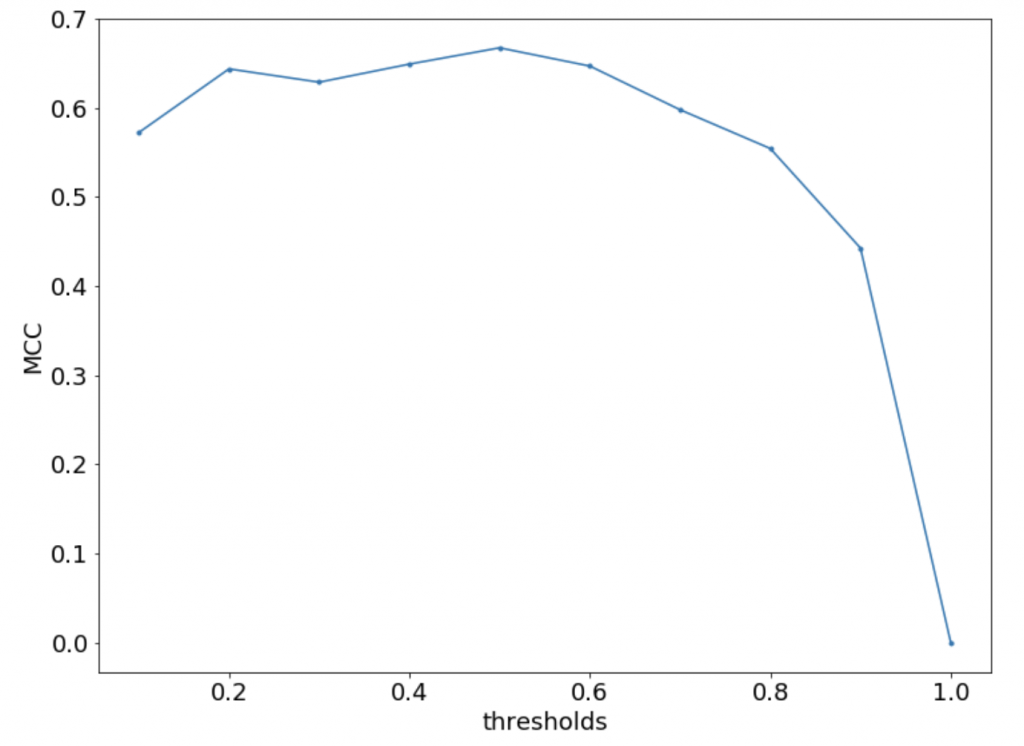
でわコードを貼って終わりにします。
パラメータ空間は位相空間。でわ