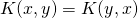こんにちは。
今回はカーネルについてです。カーネルといえば次元削減がもっともポピュラーな関連ワードなんじゃないでしょうか。なぜカーネルなのか、どうやって働いているのか、について少し考察してみます。
そもそもカーネルとはなんなのか?という問いに対しては
ある空間(主に高次元)での内積を計算する手法
が答えになります。では次に来るのはなぜ内積を計算したいのか?という問いです。
 https://commons.wikimedia.org/wiki/File:Kernel_yontemi_ile_veriyi_daha_fazla_dimensiyonlu_uzaya_tasima_islemi.png
https://commons.wikimedia.org/wiki/File:Kernel_yontemi_ile_veriyi_daha_fazla_dimensiyonlu_uzaya_tasima_islemi.png
データを扱う際、別に高次元だけでなくあらゆる空間で内積をとるという行為はあちこちで必要となります。これについてはSVMの実装とか色々勉強してみるとわかります。つまり、先走ると、データを別次元で扱いたいさいはその内積さえわかればいいことが多いんです。
内積だけでいいのか??
と絶対思いますよね。上の図でいえば写像
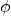
を知る必要なしに、右側のFeature Spaceで左側のInput Spaceのデータを扱うことができるなんてあり得るのでしょうか?それがあり得るんです。 みていきましょう
写像
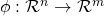
を画像左側から右側へのものとします。すると、特徴空間での
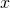
と
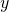
の内積は
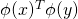
となります。つまり、カーネルは次のようになります。
![Rendered by QuickLaTeX.com \[K(x,y) = \phi(x)^T\phi(y)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-9aceadfad99cc3015ecc3f7e19a6237d_l3.png)
これだけではわからないので具体例を見ましょう。すればわかります。
![Rendered by QuickLaTeX.com \[K(x,y) = (x^T y)^2\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-9086d3d56a4bff6147224d1d1a422ea9_l3.png)
上のカーネル関数を考えます。これを分解していきましょう。つまり
![Rendered by QuickLaTeX.com \[K(x,y) = \left( \sum_{i=1}^{n}x_i y_i \right)\left( \sum_{j=1}^{n}x_j y_j \right)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-3dad6aafd1a53f146d7dbe8b996e1614_l3.png)
![Rendered by QuickLaTeX.com \[= \sum_{i=1}^{n}\sum_{j=1}^{n} x_i x_j y_i y_j\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-27b6446b5c3cabb4e9d15868bd7f6a89_l3.png)
![Rendered by QuickLaTeX.com \[= \sum_{i,j=1}^{n} (x_ix_j)(z_i y_j)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-afa083fe1c27065db7e34882da2dade8_l3.png)
とします。もうわかりましたでしょうか。例えば
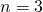
とすると
![Rendered by QuickLaTeX.com \[ \bm{\phi(x)} = \left[ \begin{array}{c} x_1x_1 \ x_1x_2 \ x_1x_3 \ x_2x_1 \ x_2x_2 \ x_2x_3 \ x_3x_1 \ x_3x_2 \ x_3x_3 \end{array} \right]^T\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-bc2126902a8619e9f86d3db0d2e47e8b_l3.png)
ということになります。つまり、この例だと写像
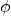
は上のようなものであり、特徴空間は9次元だったということです。ちなみにこのカーネル関数を線形カーネルと言います。もう一例みましょう。
![Rendered by QuickLaTeX.com \[K(x,y) = (x^T z + c)^2\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-c1f03151096f46e96ae425f19dd3f288_l3.png)
同様に分解すると
![Rendered by QuickLaTeX.com \[= \sum_{i,j=1}^{n} (x_ix_j)(z_i y_j) + \sum_{i,j=1}^{n} (\sqrt{2c}x_i)(\sqrt{2c}y_i) + c^2\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-6f50e0d793318c2c281b6551418cd415_l3.png)
で
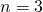
のとき
![Rendered by QuickLaTeX.com \[ \bm{\phi(x)} = \left[ \begin{array}{c} x_1x_1 \ x_1x_2 \ x_1x_3 \ x_2x_1 \ x_2x_2 \ x_2x_3 \ x_3x_1 \ x_3x_2 \ x_3x_3 \ \sqrt{2c}x_1 \ \sqrt{2c}x_2 \ \sqrt{2c}x_3 \ c \end{array} \right]^T\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-0d1aa844f9af7dc43be7f88de3984875_l3.png)
見ての通り13次元の特徴空間であることがわかります。一般化すると
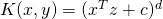
は
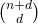
次元でのカーネルになります。
ここまででカーネルがでたらめではなく、ちゃんと高次元での内積を計算してくれていることがわかりました。では次の疑問としてどういったカーネル関数ならいいのか?が現れます。実はここが非常に難しいのです。
Mercer’s Theorem
Reproducing Kernel Hilbert Space (RKHS)
これらがキーワードになります。特に上の定理について
- symmetry:
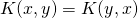
- Positive semi-definiteness
を満たす必要があります。
カーネルが何か、そして何をしているのかわかったかと思います。面白いカーネル関数がわかれば僕に連絡ください。笑
Reference

![]()
![]()
![Rendered by QuickLaTeX.com \[K(x,y) = \left( \sum_{i=1}^{n}x_i y_i \right)\left( \sum_{j=1}^{n}x_j y_j \right)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-3dad6aafd1a53f146d7dbe8b996e1614_l3.png)
![Rendered by QuickLaTeX.com \[= \sum_{i=1}^{n}\sum_{j=1}^{n} x_i x_j y_i y_j\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-27b6446b5c3cabb4e9d15868bd7f6a89_l3.png)
![Rendered by QuickLaTeX.com \[= \sum_{i,j=1}^{n} (x_ix_j)(z_i y_j)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-afa083fe1c27065db7e34882da2dade8_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[= \sum_{i,j=1}^{n} (x_ix_j)(z_i y_j) + \sum_{i,j=1}^{n} (\sqrt{2c}x_i)(\sqrt{2c}y_i) + c^2\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-6f50e0d793318c2c281b6551418cd415_l3.png)
![]()