こんにちは。

本日はアップリフトモデリングやっていきます。こちらも傾向スコア分析と同様にマーケティングの分野で使われる機械学習的な手法です。ちなみに論文の原本はこちらです。
まず前回の復習を行い、今回のアップリフトモデリングとの違いをはっきりさせましょう。
傾向スコア分析
復習です。傾向スコア自体はバランシングスコアの特殊形として定義される実数でした。その実数を出力する関数(モデル)としてロジスティック回帰を使うのでした。こうして得られた傾向スコアがRubinのSUTVAを満たしてくれるおかげで、「もしTreatmentを受けていたら〜」の代替として扱えるのでした。
今回のアップリフトモデリングは少し異なります。名前の「アップリフト」からわかるように費用対効果を最大化するためのモデリングです。つまり、どういったユーザーをTreatすれば無駄なく効果を最大化できるかをモデリングします。一方で傾向スコア分析は因果効果の推定方法です。
Who is Target ?
上のセクションで述べた「どういったユーザー」について確認します。Rubinのモデルを思い出してください。「もし〜だったら」も含めたユーザーの行動の有無を考えると行動パターンは次の4種類になります。
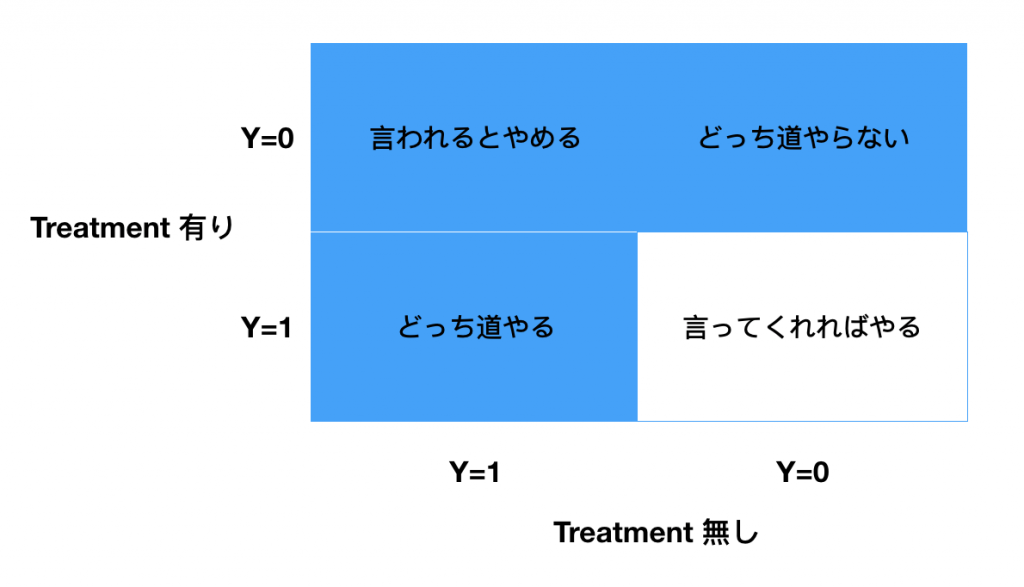
前回のサイゼリアを例にするとTreatmentはクーポンの配布です。ラベル![]() がサイゼリアに行ったか、行かなかったかです。アップリフトはこのクーポンの費用対効果を最大化させるための指標です。
がサイゼリアに行ったか、行かなかったかです。アップリフトはこのクーポンの費用対効果を最大化させるための指標です。
見ての通り、図中の白い部分のユーザーを対象にクーポン配布することが最も効果的であることがわかります。
Two-Model Approach
ではそのアップリフトの定義です。
The uplift is defined as the difference between success probabilities in the treatment and control groups.
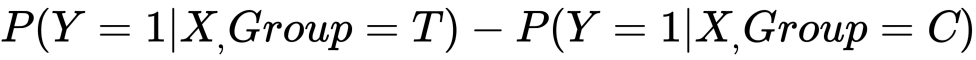
見ての通りこれは各集合における成功確率の差です。(モデルはそれぞれ定義します。)したがってアップリフトモデルは
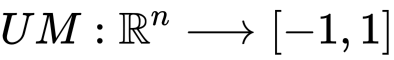
として定義されます。ちなみに、参考文献ではアップリフトを差ではなく、割合として定義されていました。おそらくどちらでも構わないと思いますが、この記事では論文にしたがって差として話を進めていきます。(割合にすると理論上は無限まで飛びます。)
また、先ほどの図とこのUMの値を共に考えていただきたいのですが、UMが大きいとはつまり、P(Y=1|X, G=T)が大きく、P(Y=1|X, G=T)が小さいことを意味します。これはまさに図中の白い部分に相当します。逆も同様です。したがってアップリフトが費用対効果最大化の指標として素晴らしいことがわかります。
AUUCとLIFT
AUUCはアップリフトモデリングの指標になります。
The Area Un- der the Uplift Curve (AUUC) can be used as a single number summarizing model performance.
AUCのように面積が広い方が精度が高いことを意味します。このAUUCの導出の際にLIFTと呼ばれる値を用います。AUCがどうやって導出されたかを思い出して考えます。AUCは無数の閾値で与えられたグラフでした。さらにTPRとFPRに対してトレードオフの性質を持っていました。AUUCも同じようなものです。
アップリフト上位の![]() 個のサンプルに対して次がliftになります。
個のサンプルに対して次がliftになります。
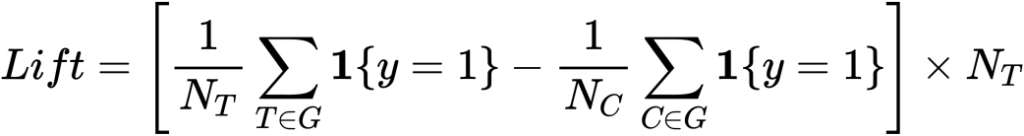
N_TはTreatmentの総数です。またベースラインはアップリフトの上位ではなくランダムで算出した値になります。
ここで考えます。アップリフト上位のデータ群に対するLIFTは右上がりになりますよね。これは先ほどのUMの写像の際の説明からわかります。となると逆も然りです。つまり、アップリフト下位のデータ群はLIFTは右下がりになることが予想できます。したがって最終的にAUUCのグラフはAUCと同様に凸関数のような形になり、その頂上を刺す時のUPLIFTが閾値として最適であると判断できます。(AUUC図のx軸はアップリフトの降順、y軸はLIFT)AUUC自体はbaselineとliftに囲まれた実数になります。
ここまでのTwo-Model ApproachではTreatmentとControlのそれぞれについてmodelを用いて![]() を予測しました。しかし、二つのmodelを用いることによってパラメータチューニングが難しくなるなどの問題点があります。共変量シフトがあるかもしれないので。そこで単一のモデルのみを用いたClass Variable Transformationについてみてみます。
を予測しました。しかし、二つのmodelを用いることによってパラメータチューニングが難しくなるなどの問題点があります。共変量シフトがあるかもしれないので。そこで単一のモデルのみを用いたClass Variable Transformationについてみてみます。
Class Variable Transformation
とはいえ単一のモデルでどうやってアップリフトを定義するのでしょうか。非常に気になります。文字がかなり出てきますが頑張っていきましょう。
まずは次の変数を導入するところからです。
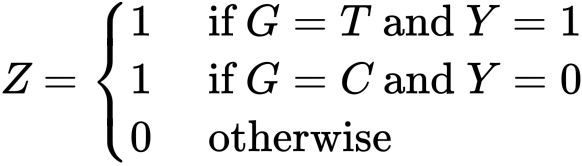
これを用いて先ほどと同じように![]() について確率を計算してみます。
について確率を計算してみます。
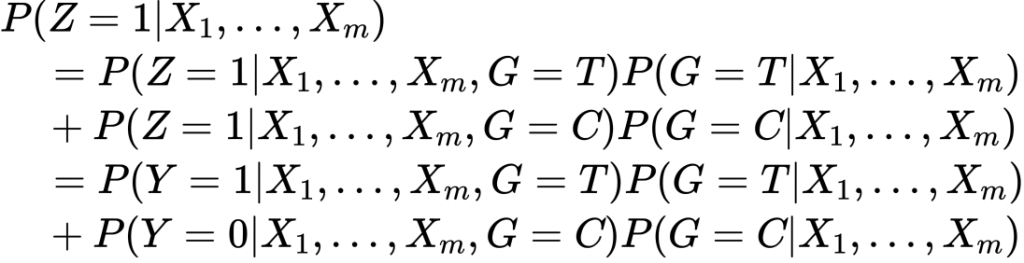
ここで割り当ては無作為を仮定します。これ重要。したがって
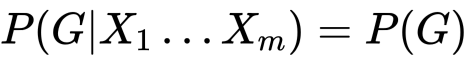
こちらも必要な仮定になります。
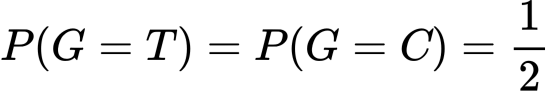
また、次も成り立ちます。
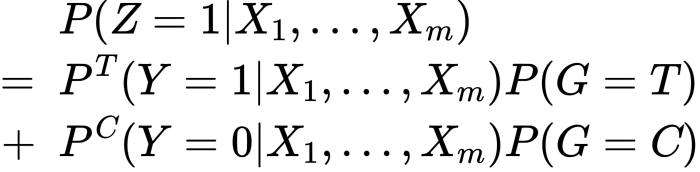
すると次が得られます。
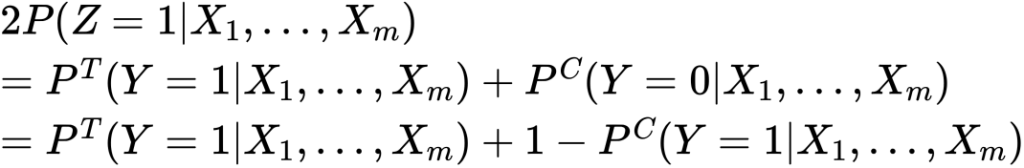
お、できました、移項すると
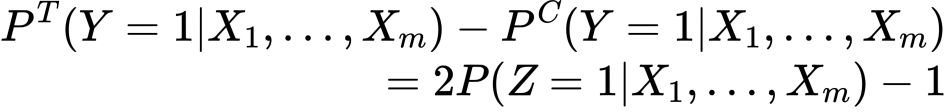
つまり新しく導入した![]() が1になる確率を予測するモデル一つで先ほどと同じようにアップリフトが算出できるということです。
が1になる確率を予測するモデル一つで先ほどと同じようにアップリフトが算出できるということです。
ちなみにAUUCとLIFTはアップリフトモデリングの指標なのでこちらのアプローチにももちろん使えます。
アルゴリズムの比較
まずはAUUCです。
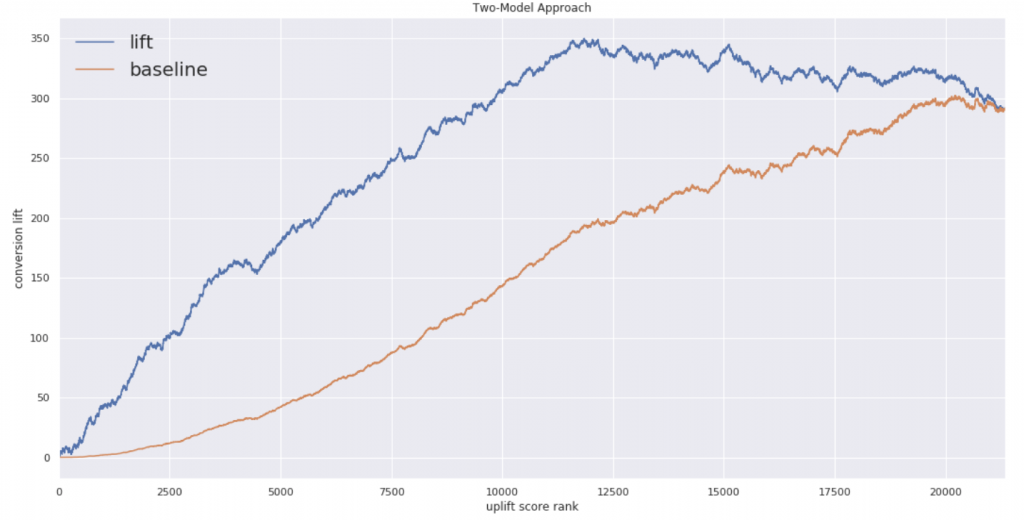
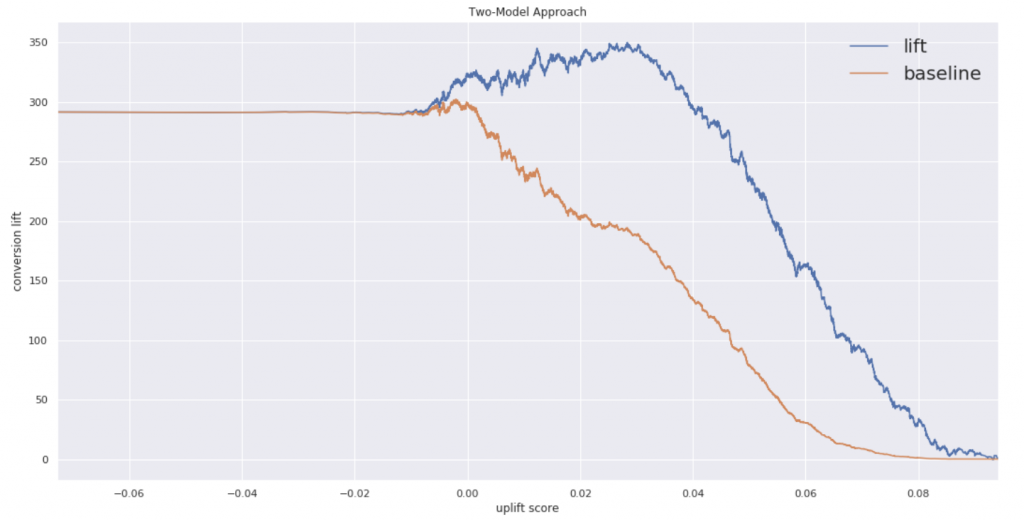
閾値としてのアップリフトスコアは0.03あたりが良さそうです。ちなみにスコアと各確率は次のような感じ
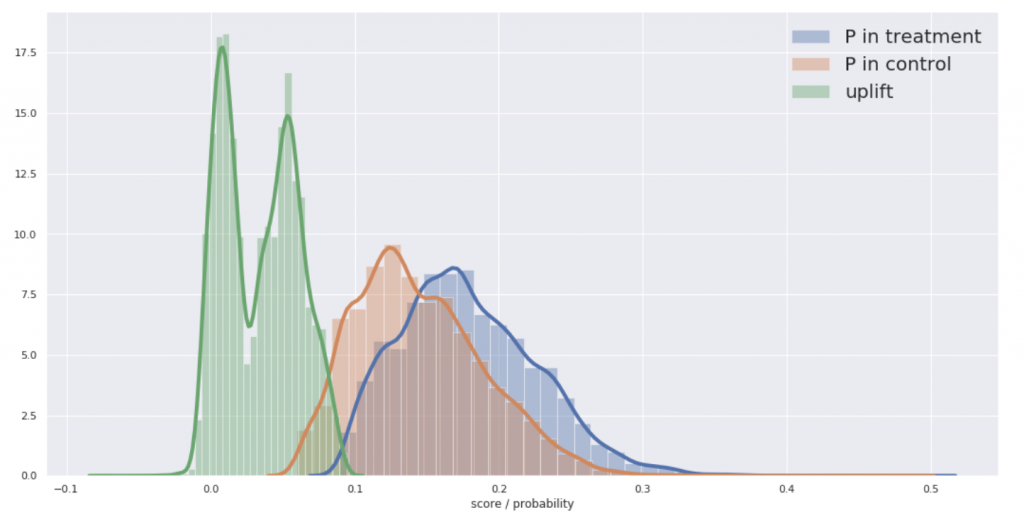
先ほどのグラフで原点より左が潰れていることがここから確認できます。ではもう一方のアルゴリズムでも確認してみます。
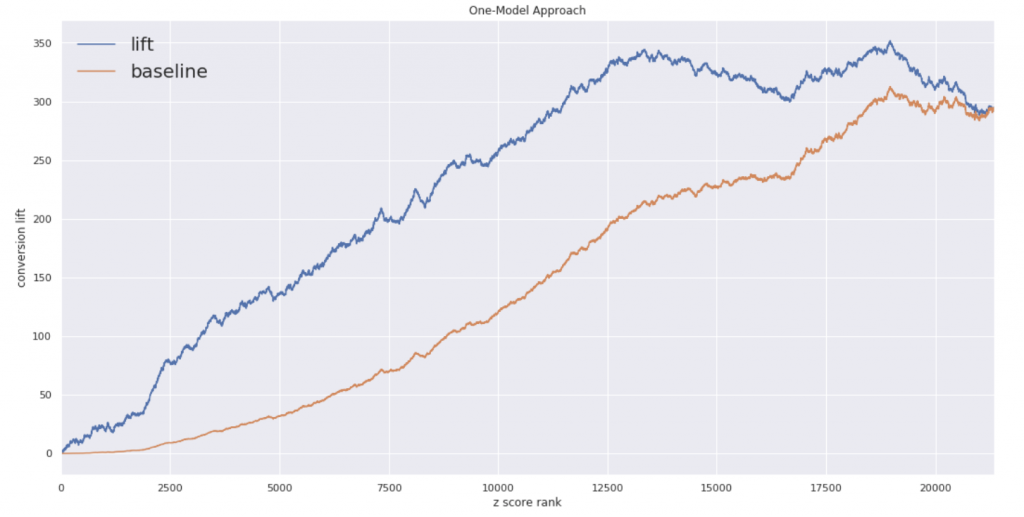
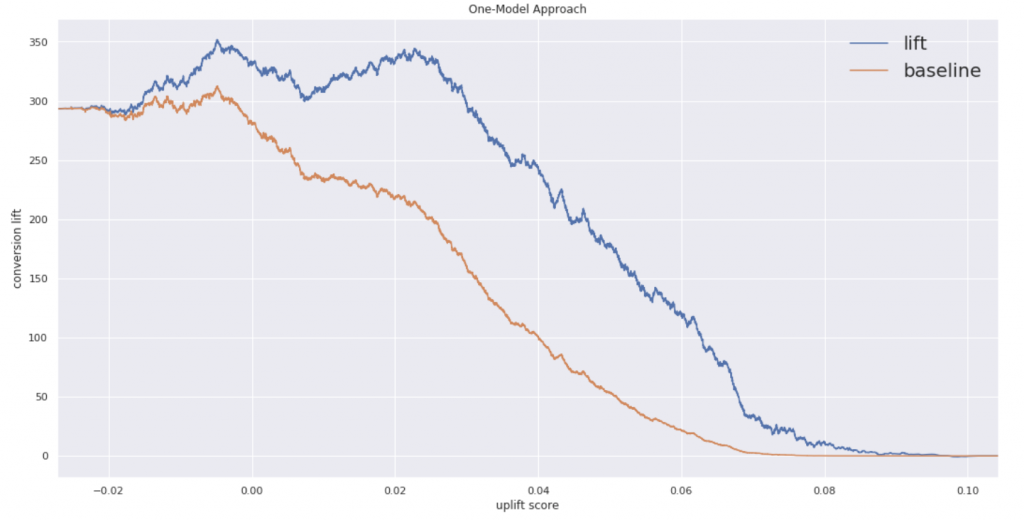
シングルモデルのおかげか綺麗なグラフになっています。ちなみにコンバージョン率のパーセンタイル分布は以下のようになってます。
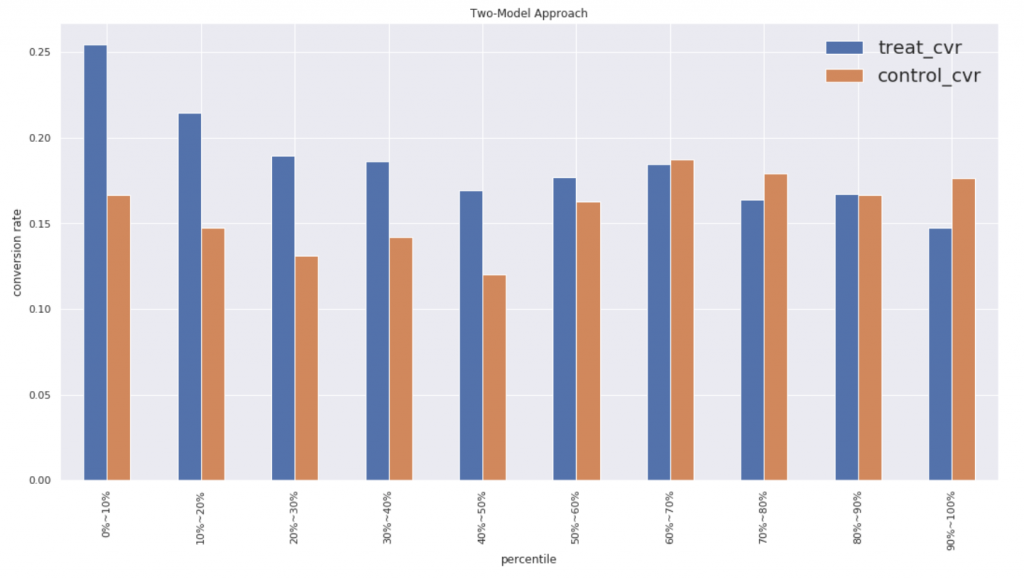
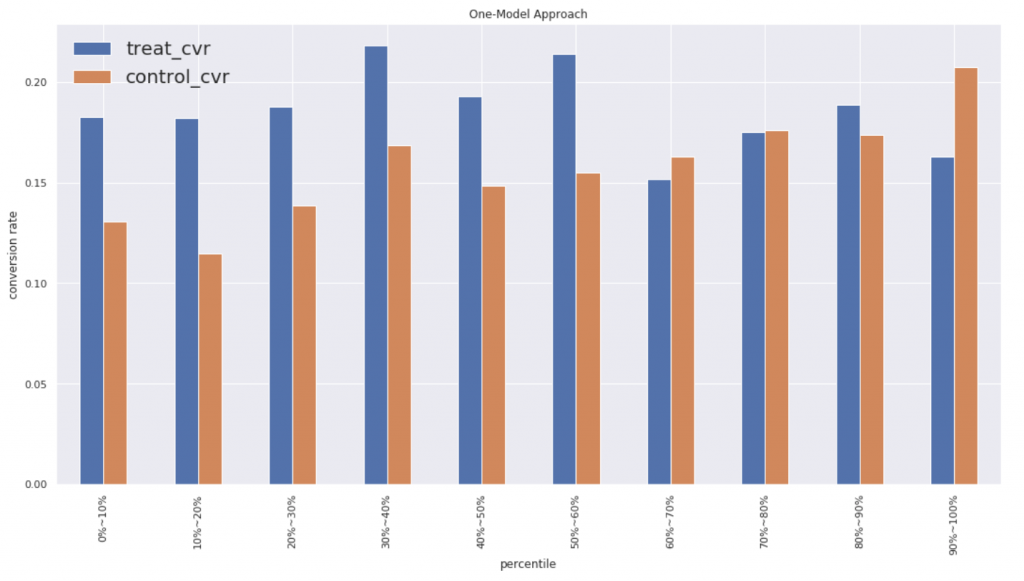
シングルモデルの方が上位60パーセントにおいてTreatの効果があることがわかります。
長くなりましたが実装貼っておきます。
一般化傾向スコア分析が難しすぎます。でわ