こんにちは。kiwamizamuraiです。

本日はダブルロバストについて勉強します。まぁ、IPWも厳密には理解できていないんですけどね。。。。僕の勉強スタイルはとにかく大きく進んで大きく戻っての繰り返しです。するとたまにぱってアイデアが生まれてわかる時があります。まあそんなことはおいておいて

Recap

この記事ではダブルロバストの理論について触れます。その前に前回のIPWの復習も行い、新しい知見が得られることにも個人的に期待します。

ただ、Counterfactual Machine Learningにもダブルロバストが登場して用語などが非常にごっちゃになりやすいところだと思うのでそれについてもまとめます。

  • Multi-Arm Bandit Algorithm
  • Reinforcement Learning
  • Counterfactual Machine Learning
  • Causal Inference

ここら辺は正直ごちゃまぜになっている気がしますね。。。。。さきに断りますが今回のダブルロバストは因果推論におけるものを指します。反事実機械学習のポリシー評価に対するダブルロバストではありません。

因果推論の復習

僕たちが測りたい因果効果はATE(Average Treatment Effect)といいます。

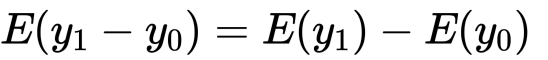
ちなみに割り当てがされた、つまり処置群における平均処置効果はATTといいます。

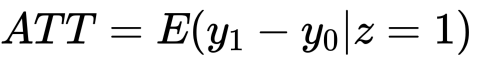
ATEについては各群間での効果量の差をとればいいじゃん、という単純な案がありましたが駄目でした。それはoutcomeであるyの期待値が確率収束するものの条件付きの値だからです。つまり、上記のATEではないということです。そこでRubinのSUTVAの仮定のもとで因果効果を「無作為割り当てでないことによるバイアス」を消去しつつ測ろうというものでした。

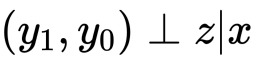
そして登場するのが傾向スコアです。yに対してセミパラメトリックなアプローチができ、モデルの誤設定の可能性が低まります。また、N次元であった共変量が1次元になることでその影響も排除することができます。

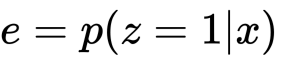
この傾向スコアはSUTVAを満たしてくれるので等しい傾向スコアのもとで


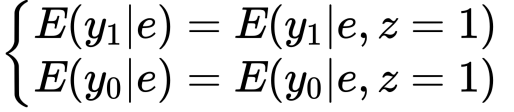
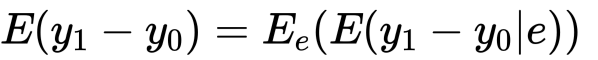
が成り立ち、

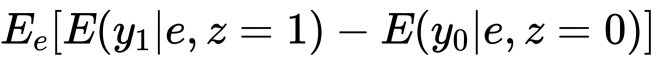
がATEであることがわかります。少し補足をしておきます。

傾向スコアのモデルはロジスティックが一般的ですが、RFなどのアルゴリズムも使用可能です。ただ、その後たとえばマッチングを行うと仮定するとRFの高精度な分類により各分布が大きくことなる可能性があります。この場合、マッチングがうまく働かないかもしれません。なので個人的にはロジスティックがいいかなと思います。

Inverse Propensity Score Weighting

最近傍マッチングと層別解析については触れません。ここではIPWの復習を個人的に行います。このアルゴリズムは無作為割り当ての問題を解決しつATEを算出することができます。では解説します。

真の傾向スコアが既知かつSUTVAが成り立つとする。


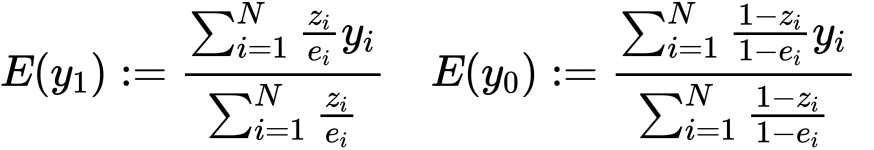
このとき、上のように定義することでそれぞれy1,y0の周辺平均の不偏推定量となります。さらに、我々が算出する傾向スコアに対してもタイスの法則よりこれらは一致推定量になります。（ちなみに分母を集合の濃度Nで代用する方法もありますがこちらのほうが精度は高いことがしられています。）次のセクションではこの意味について考えてみます。

Pseudo-population

eは傾向スコア、つまり確率です。この逆数を重みとする、というのはどういう意味があるのでしょうか？例えば0.1の逆数は10です。0.8の逆数は1.25です。

これはつまり確率を割合として考えれば個人的にはわかる気がします。つまり、各群の集合の濃度を傾向スコアの逆数で補正しているということです。Inverse Weightingの値をPseudo-populationといいます。たとえばマッチングにおける問題点の一つは分布差でした。つまり。個体数が異なります。この個体数差をInverseで重み付けという形で加味できるということです。

Doubly Robust

では個人的に本題のダブルロバストについてです。これは二つのモデルを仮定してどちらか少なくともどちらか一方が正しければうまくいく、というものです。二つのモデルのうちの一つは単純な回帰によるATEの推定モデルです。

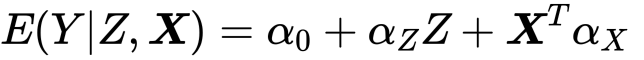
これはyの真のモデルであればの話です。そしてもう一つはIPWを使った上記のものです。

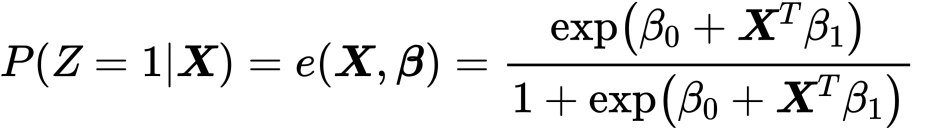
こちらは傾向スコアを通したATE測定のためのモデルでした。ダブルロバストはこれらを融合します。つまり、yとeのモデルを融合するということです。DR(Doubly Robust)はこれらのモデルによって得られたe,y_1y_0を用いて算出されます。

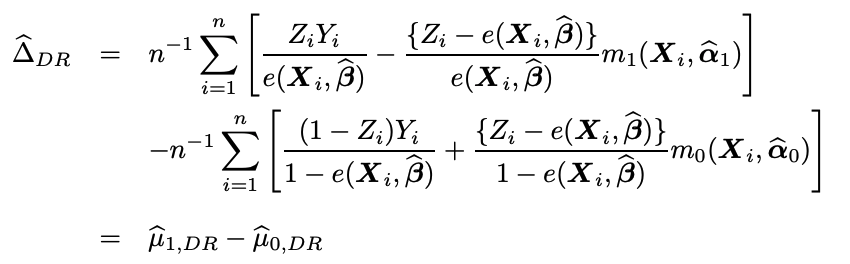
計算式は上の通りです。シグマの前の1/nはIPWのセクションで述べた理由からです。デルタはATEのことです。非常にややこしい式ですね、、、少しずつみていきます。

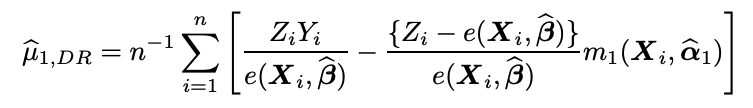
この大括弧内の初項はIPTW、第二項はAugmentationと呼ばれます。とりあえずこの期待値をみてみましょう。

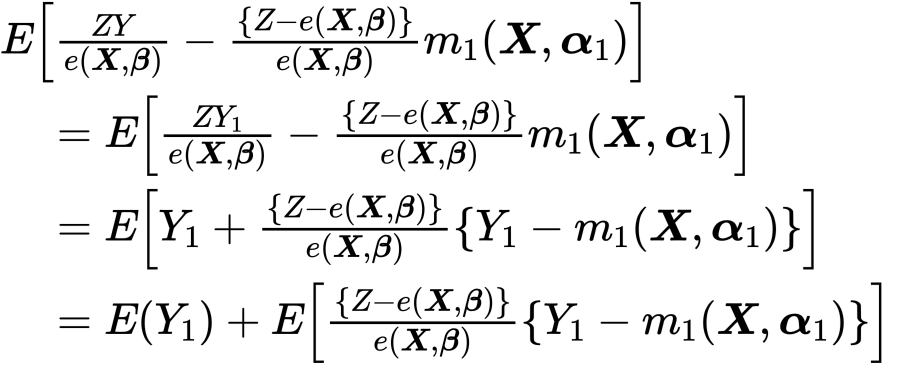
つまり、第二項がゼロでいてくれればE(Y1)が推定できます。ではどのような時がゼロになってくれるのか？ここでダブルロバストが生きます。

まず、傾向スコアが正しくて、回帰モデルが誤っている場合。つまり、

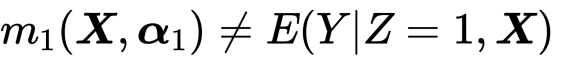
であり、傾向スコアが真であるとき、

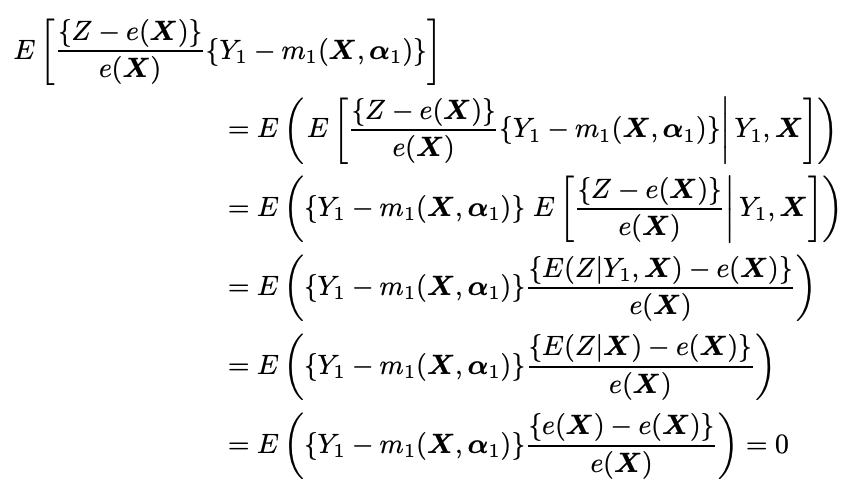
とうまく第二項が消えてくれました。わーい。E(y0)も同様です。では逆の場合を考えましょう。つまり、傾向スコアが誤っていて、回帰モデルが正しい場合

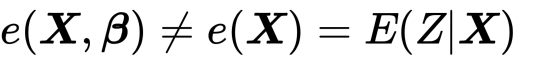
であり、回帰モデルmは正しい時、同じように第二項は

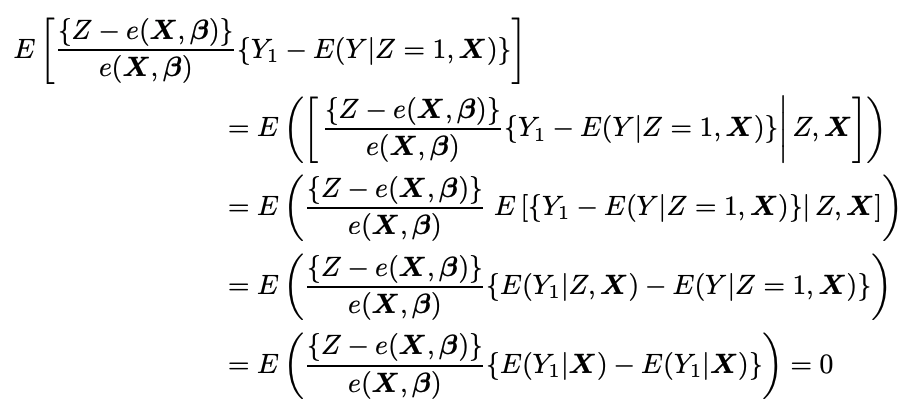
となります。こういう意味でダブルロバストと言われています。ちなみにですがこの推定方法をAugmented IPTWといいます。AIPTWです。

実装

データは前回と同じものを使いました。IPTWとAIPTWを比較するとわずかですが今回はIPTWが勝ちました。また、分母に集合濃度Nを用いると大きく精度が悪化しました。

次は反事実機械学習のダブルロバスト！

References