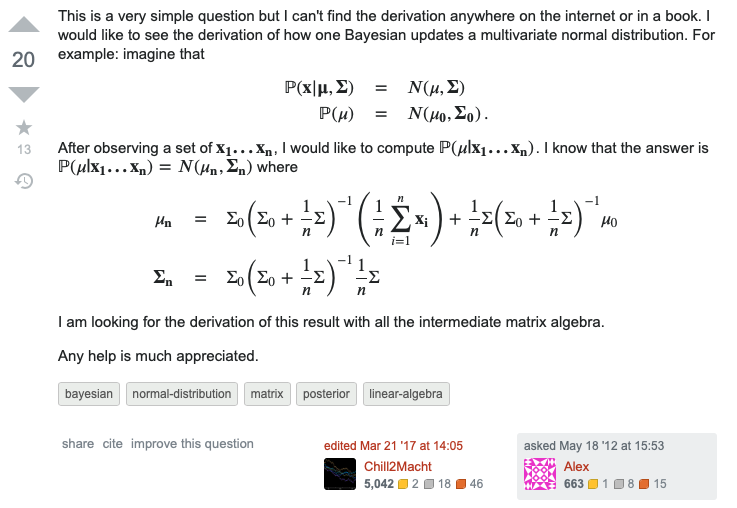
こんにちは。

本日は文脈バンディットをやっていきます。行列とかでてきて、、、、計算が苦手な僕は、、、って感じなんですけどやってることは前回のUCBをTSと全く同じなので気楽にいきましょう。

Contextual Bandit

文脈バンディットとは以前のバンディット問題にユーザーの特徴量ベクトルを導入されたものです。というとは、前回は単純に時刻tにおいて行動価値関数のみでアームを選んでいましたが、文脈バンディットではユーザーの情報も加味してアームを選ぼうという考えです。

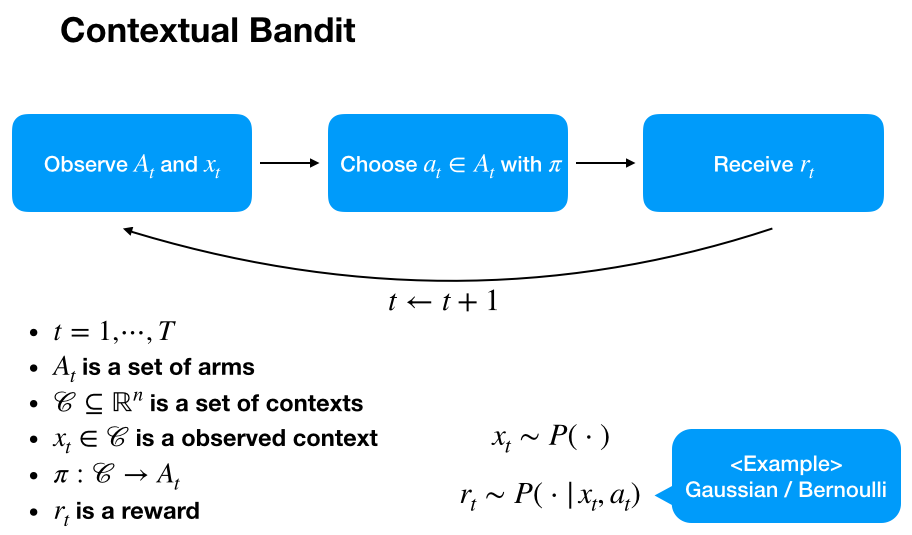
アルゴリズムに入っていく前に具体例と一緒にこの文脈バンディット問題の全体像を掴みます。

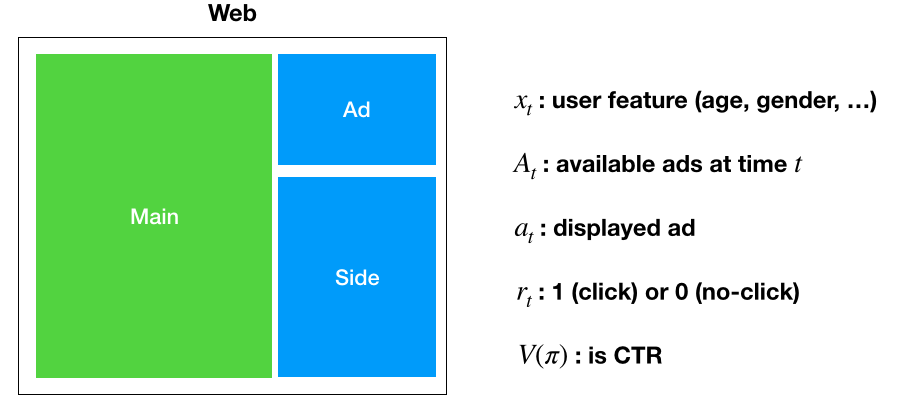
たとえば上の図のような感じです。報酬は購入額（例えば正規分布）とかでもいいです。とりあえず問題設定はできました。

ポリシーに対するoffline評価などはまた次回やりたいと思います。今回は単純に次の二つのポリシーの実装のお話です。

LinUCB

まずLinUCBとは前回したUCBの文脈バンディットへの拡張アルゴリズムです。この時点で上界・分散的なイメージをもって欲しいです。また、Linearの略です。見ていきます。（添字a,tは時刻tにおける行動aに対する、という意味）

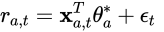
LinUCBのLinearの部分はここからきています。LinUCBは報酬に対して上記の線形モデルを仮定します。また、ノイズとしてsub-Gaussianを乗せます。すると期待値は次の通りです。

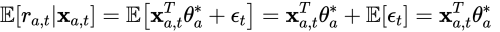
このように行動aに対して確率分布を仮定し、さらにそのパラメータを逐次的に更新することでより柔軟なアームの選択が可能になります。ではそのパラメータの更新式を導出します。

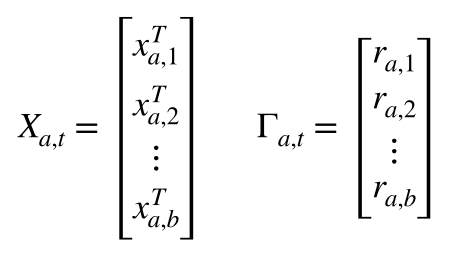
上のように定義します。するとbiased-MFまたはRidgeの時と同じ導出より

次が得られます。

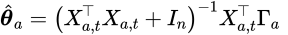
次にUCBの部分についてです、

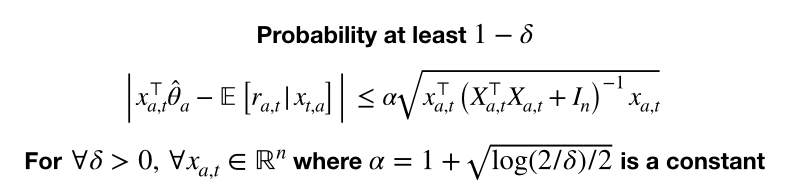
どうやら上は定理のようです。そこまで終えませんでした。すいません。とはいえこれがわかったので前回のUCBを思い出してUpper Boundを加算してアームを選べばよいだけです。

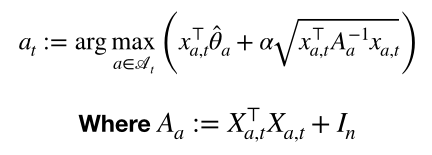
まあA_aは共分散行列とやらですね、inverseをとる点だけ注意していればおkです。では改めましてpresuso-codeは

いい感じですね。ちなみにハイブリットモデルというバージョンのものもあります。

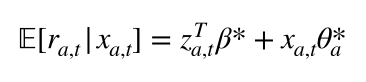
ハイブリッドでは上のように報酬に対する線形モデルが少し変わります。これは前回実装したbiased-MFと全く同じ発想で、zはユーザーの特徴ベクトル、betaは全アームに共通する共有ベクトルと行った感じです。（勝手に命名しました。）presudo-codeも貼っておきます。

でわLinear Thompson Samplingも見ていきましょう

LinTS

これは前回のTSと全く同じで事後分布からパラメータシータをサンプリングする方法です。 ただ、論文中の事前分布とかは結構複雑で結果的に次のpresudo-codeになってます、

ガウス分布を仮定していますが、パラメータが複雑なので簡略化しましょう。なので上の疑似コードは一旦無視です。

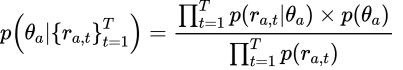
とりあえずベイズを使って上を分解していくんですけど、ここでは事前分布としてsub-Gaussianを仮定します。

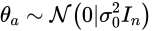
尤度は今回の場合だとガウス分布です。（最初の線形モデルの仮定より）

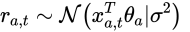
となると事後分布なんですけど、「ガウス x ガウス = ガウス」なのですが、、、、、問題は多次元なんですよね、、、、僕計算めちゃめちゃ嫌いなんですよね、、、、

https://stats.stackexchange.com/questions/28744/multivariate-normal-posterior

って感じで、一応サンプリングできます。

LogisticTS

ただ、前回実装したbanditって報酬はベルヌーイを仮定したじゃないです か、ということはcontextualにもあるはずですよね。

モデルは簡単です、先ほどの線形モデルにロジスティックをかますだけです。

https://arxiv.org/pdf/1508.03326.pdf

そうなんです、あるんです、ただロジスティックを使ってしまうと事後分布が解析的には得られないので勾配法とかになっちゃうところをラプラス近似でやろう！という発想です。僕はラプラス近似をあまり知らないのでそれも勉強しないといけませんが、とりあえず話を進めると事後分布は正規分布になるようです、さらに共分散行列は対角行列らしいです。presudo-codeは次のとおりです。

ぎょえええって感じですね、これを実装しなければいけないのか、、、、

実装

実際の報酬のアームの分布は次の通りです。

LinUCBの結果

LinTSの結果

パラメータを変化させてRegretも確認

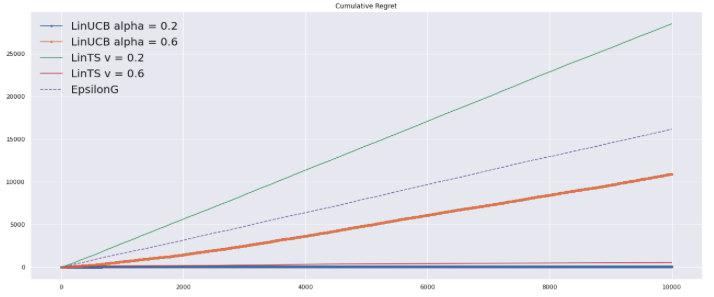
ちょっと疲れました。

ロジスティックはまた今度機会があればやります。

References