こんにちは。kzです。

世の中ではやはり解釈性が重要らしいです。

前回、SHAP含めてモデル解釈の指標についていくつか触れました。やはり一度では僕は残念ながら理解できないので復習も含めて今回この記事を書きます。

前回の復習

上記のリンク先が前回の記事になります。

  • Permutation Importance
  • Partial Dependence
  • LIME
  • SHAP
雑におさらいするとPIは対象の変数をシャッフルして精度の変化からその変数の影響力を見る手法。PDは対象の変数以外を周辺化で消すことによってその変数のみの影響力を見る手法。LIMEは対象の入力データ周辺でブラックボックスモデルを線形近似しその重みでそれぞれの変数の寄与具合を見る手法。SHAPはLIMEのモデルに複数の制約（Consistencyなど）を与えてできた特殊な距離を使った手法（LIMEの上位互換）

ちなみに他にもDrop-Column Importanceとかもあるらしいです。

Feature Importance

順番的には逆になってしまいましたが、決定木自体にはFeature Importanceというものがあります。ご存知ですよね。どうやって算出されてるのや？と思ったので調べました。結論から言えばあまりにも式が複雑で完全に理解し切るのはかなりハードです。。

なのでその計算の核となるGini Impurityから始めます。

Gini不純度

あるノードにおけるGini不純度は上のように定義されます。記号については以下の通り

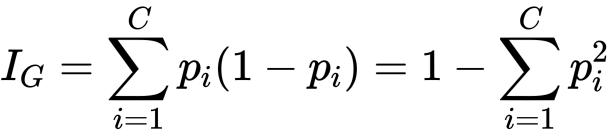
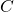  • Cはクラスの総数
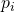  • p_iはクラスiの割合
分類においては各ノードではできるだけ少数のクラスであって欲しいですよね。具体的に計算してみます。 
         二郎系   家系  　  まぜそば 
count =  4       4        4 
p     =  4/12    4/12     4/12       
      =  1/3     1/3      1/3 
GI    = 1 - [ (1/3)^2 + (1/3)^2 + (1/3)^2 ]  
      = 1 - [ 1/9 + 1/9 + 1/9 ]    
      = 1 - 1/3    
      = 2/3   
      = 0.667
各クラスから均等な量の場合とあるクラスに偏りがある場合 
         二郎系   家系  　  まぜそば 
count =  3       3        6 
p     =  3/12    3/12     6/12   
      =  1/4     1/4      1/2 
GI    = 1 - [ (1/4)^2 + (1/4)^2 + (1/2)^2 ]
      = 1 - [ 1/16 + 1/16 + 1/4 ]
      = 1 - 6/16   
      = 10/16    
      = 0.625
少し小さくなりました。ではあるノードにおいて単一のクラスのみある場合はどうでしょうか。 
         二郎系   家系  　  まぜそば 
count =  0       12        0
p     =  0/12    12/12     0/12
      =  0       1         0 
GI    = 1 - [ 0^2 + 1^2 + 0^2 ]
      = 1 - [ 0 + 1 + 0 ]
      = 1 - 1
      = 0.00
0となりました。きれいに分類できている証拠ですね。決定木のFeature ImportanceはこのGiniを用いて算出されているようです。 参考文献によると
とありました。難しいですが、要は最後の式だけ見ればなんとなくわかります。分母は前ノードにおけるImpurity Reductionの総和であり、分子は対象の特徴量jによる分岐ノードでのImpurity Reductionの総和となっています。

つまり、対象の特徴量が木全体においてどれだけGini不純度の減少に寄与できたかという指標でFeature Importanceが算出されているということです。

ということはです。分岐点を多く作りやすい変数の方が相対的にFeature Importanceが大きくなるのは直感的ですよね。単純に考えるとカテゴリカル変数よりも連続値変数の方がFeature Importanceが相対的に高まってしまうということです。さらに木を深めることで多くの分岐点が生成されるのであればその効果は莫大です。

実際Feature ImportanceにはCardinalityが密接に関係します。次にCardinalityについてみてみます。

Cardinality

みんな大好きKaggleにおいて次のような質問があった。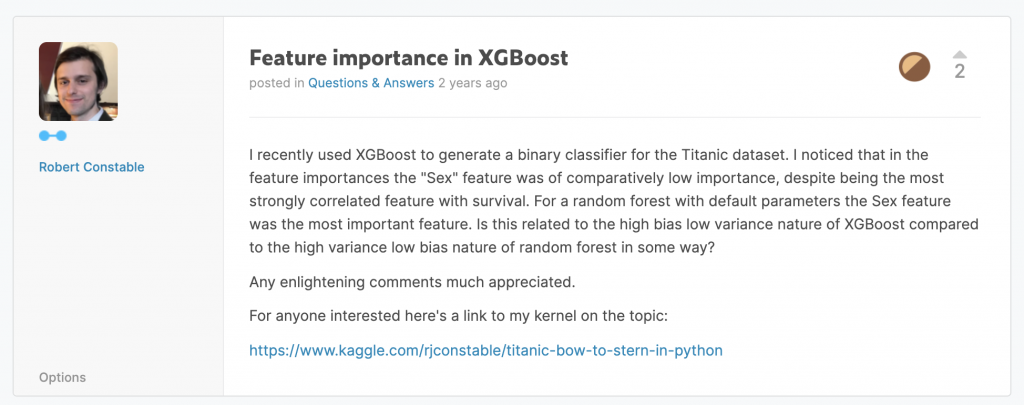
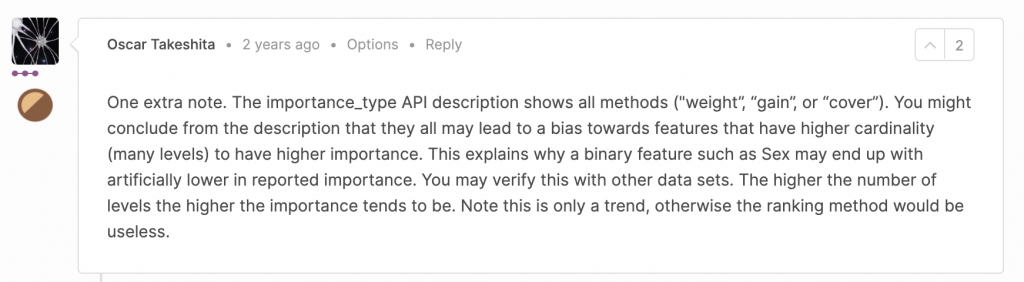
タイタニックデータをxgboostでバイナリ分類したのちfeature importanceをみた結果、特徴量の１つであるSexは目的変数と高い相関があるにもかかわらず、比較的低いimportaceが得られたらしい。 これに対して気になるコメントがあった。
なにを言っているのかというと。カーディナリティによってfeature importanceにバイアスが生じる。high-cardinalityはhigh-importanceを持つ。これが原因でSexが相対的にlow-importaceになっている。

ここでカーディナリティとは、対象の変数の多様性のこと。つまり性別のようなカテゴリカル変数よりは連続値の変数の方がカーディナリティは相対的に高い。

これはまさに上記のGiniの定義より得られた考えのことだ。よってさきほどのFeature Importanceに対する理解は正しかったということだ。

Information Gain

実は決定木における重要な指標はGini Impurityだけではなく、Information Gain（平均情報量）というものが別であります。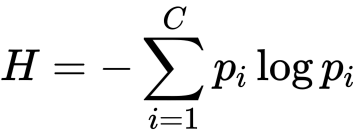
じゃあ、どっちを決定木では使うの？どっちのほうがいいの？という問に対する答えはGini Impurityです。理由は簡単で計算が楽だからです。後者を選んでしまうと対数の計算が必要になります。詳しくは次のリンクへどうぞ

LIME

じゃあ、どうしたらちゃんとした、まともな、直感的なFeature Importanceが得られるのか。という問に対する答えは僕の知るベストだとSHAPだ。もうSHAPしかない。

上述した理由から決定木におけるFeature Importanceに信憑性はない、結果的に重回帰がやはり好かれている。しかし、分類という点においては決定木やNNには重回帰では残念ながら勝てない。

最高に分類できる状態を保ちつつ、重回帰のように最高の形でFeature Importanceがほしい、という欲求を満たしてくれるのがSHAPだ。LIMEの上位互換なのでやってることはほぼ同じ。

記事の最後になりましたがここでは低次元空間においてLIMEの振る舞いを簡単に実装してSHAP（LIMEの上位互換）のイメージを理解します。下のような非線形データを考えます。
可視化に力をいれたいのでgridでデータを再度作成し、とあるインプット（青）を考えます。このインプットしたいするlimeを求めます。
LIMEもSHAPもローカルなので局所的な空間を考えます。多様体の言葉でいうとチャート、または局所座標近傍です。
距離関数としてL2距離を算出します。実際にロス関数を定義して重みを最適化するのではなく、この距離を線形回帰のライブラリのweightというパラメータに用いて外れ値を考慮した線形モデルを構築します。
前述通り今回はロス関数を定義して計算しているわけではないので厳密なLIMEの実装ではないので注意。あとは線形回帰モデルを作って重みを取得するだけです。
両軸を特徴量として扱っているので線形モデルの直線は可視化できませんが上のマークより、その振る舞いは理解できたのでわないかと思います。ピンクの部分はプラスでグレーの部分はマイナスと分類されています。その時の切片、係数も取得できます。これがlimeです。 厳密ではないですがLIMEのやっていることは理解できたかな？と思います。

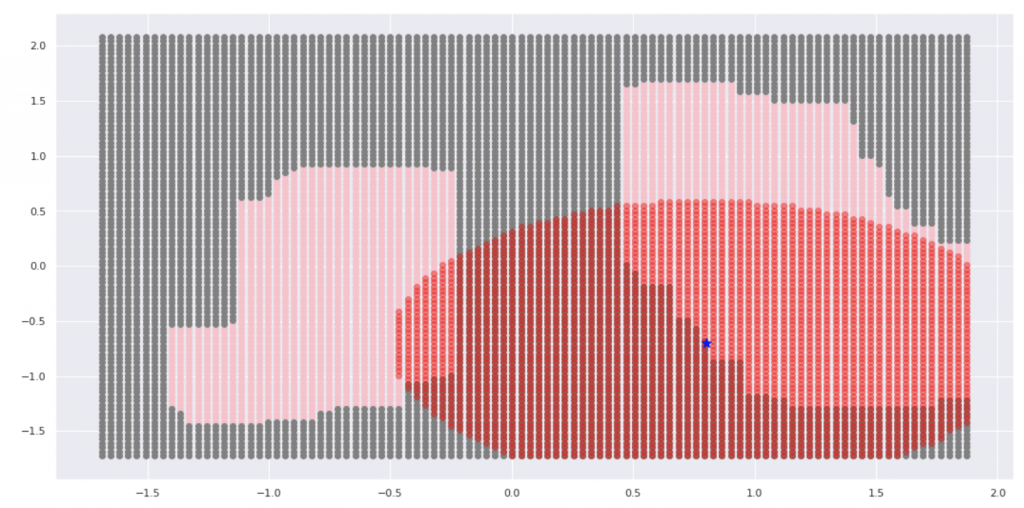
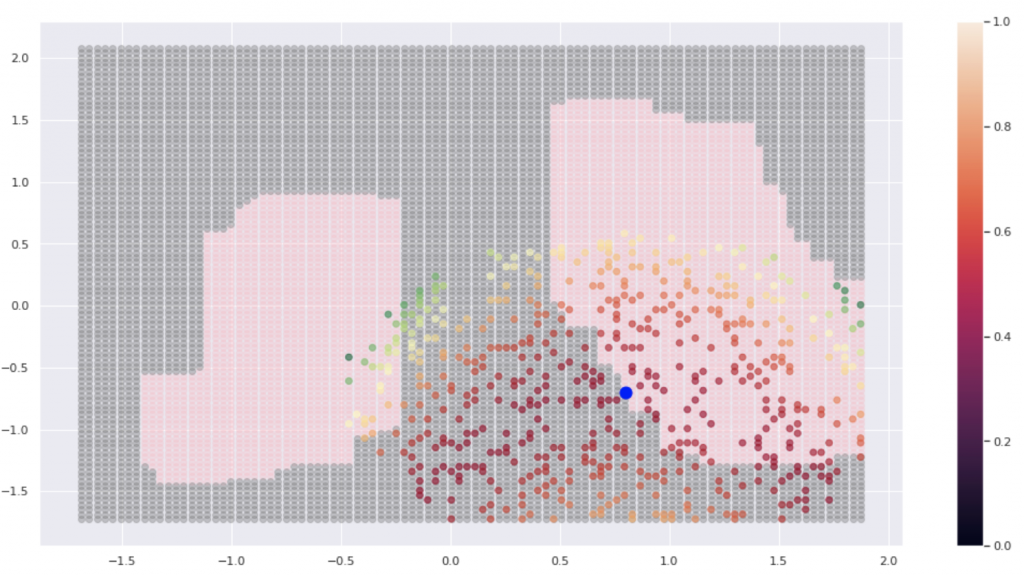
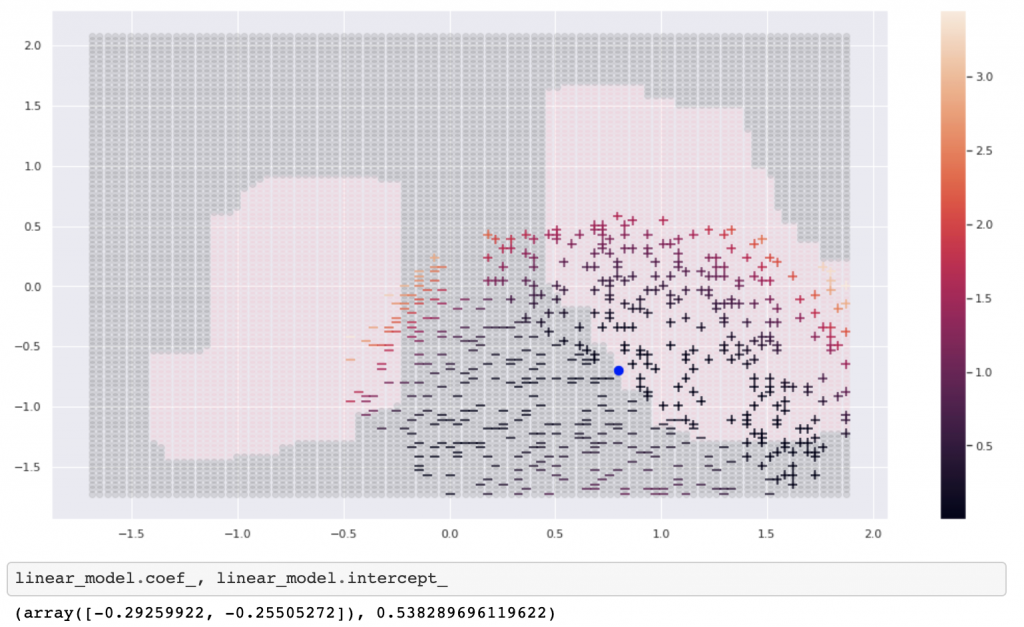
ちなみにSHAPの凄いところは制約3つめのConsistencyです。これによって対象の特徴量のFIがより重み付されます。これによって決定木におけるFIの相対的なつぶれよりも直感的なFIを得ることができます。
SHAPの距離のところがよくわからない。でわ

Reference