レコメンデーション　入門

2020.01.03

こんにちは。

本日はレコメンデーションやります。大昔にチラッと見たんですけどあの頃は興味がなくて全然してませんでした。ということで気が向いたのでやってみます。MFをメインに３つの手法を紹介します。発展版は次回の記事にします。

まずは用語からまとめます。どうやらレコメンデーションには2種類があるようです。

Recommendation System

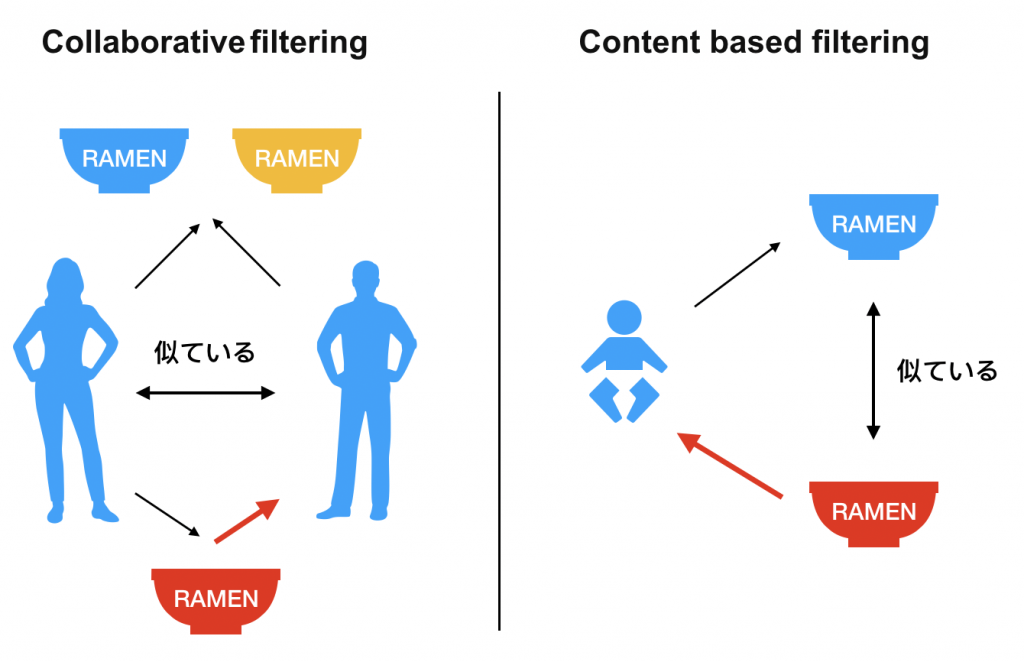
Recommendationには２種類あります。

User Based Recommender Systems
Item Based Recommender Systems

まずUser Based Collaborative Filteringについてです。Collaborative filteringは上からわかるように自分と他のユーザーの経験をデータにレコメンドします。手順は次の通りです。

[ USER x ITEM ] 行列を作成
USER間の似ている具合を計算
似ているUSERを選択
そのUSERの過去の経験からレコメンド

例えばAさんが二郎系がめっちゃ好きで通い詰めてるとします。Bさんは最近二郎系にハマり出したとします。Cさんはラーメンが好きじゃないとします。ラーメン屋の数が１０とすると行列は $3 \times 10$ になります。ここでたとえばコサインを使って距離を測ります。するとBさんはAさんと距離が近くなります。そこでAさんが過去に行った二郎系をBさんにレコメンドするという流れです。

他にも購入履歴だったり、欲しい物リストとかですね。

ただ、このユーザーベースはたとえば年齢の変化につれて趣味も変わりますし、環境によっても変わりますよね。そこでアイテムベースという考え方を紹介します。これは先ほどとステップはほぼ同じですが異なる点は距離の対象です。先ほどはユーザー間の距離を測りましたが今回はアイテム間の距離を測ります。なのでたとえば相関をとって同じようなラーメンをレコメンドしようといった流れです。

なので動画のratingやジャンルはこちらにあたります。（ratingがこっちにくるのはイマイチふに落ちませんが）

もちろん長所と短所はそれぞれあります。ここでは一部だけ紹介します。詳しくは次のリンクへどうぞ。

【レコメンド】内容ベースと協調フィルタリングの長所と短所・実装方法まとめ

行列のサイズをイメージすればわかりますが例えばアイテムが少なければコンテンツベースの方がいいです、逆にアイテムについて事前知識がなければ（ラーメンの具材など）ユーザーベースの方がいいのは自明でしょう。

ではこのくらいにして今回扱う３つの手法を簡単に説明します。他にも強強な手法がありますがまだよくわかっていないので次の記事で深入りできればなと思います。今回は触りです。

データ

その前にデータの説明ですが $User \times Movie$ の行列になります。kaggleからとってきました。各要素にはratingが入ります。たとえばaさんのスターウォーズに対するratingは4といった感じです。評価なしの要素は0で埋めます。これが今回の欠損値処理になります。今回はおすすめの映画をレコメンドすることを目的に話を進めていきます。

Correlationをとるだけの作戦

まず一つ目はcorrelationをとる方法です。映画同士の相関を計算して同じような映画をレコメンドする作戦です。簡単すぎるのでスキップします。

SVDを使う作戦

二つ目はSVDを用いて潜在的な特徴を作成し、それを使って未知のratingを計算してレコメンドする作戦です。

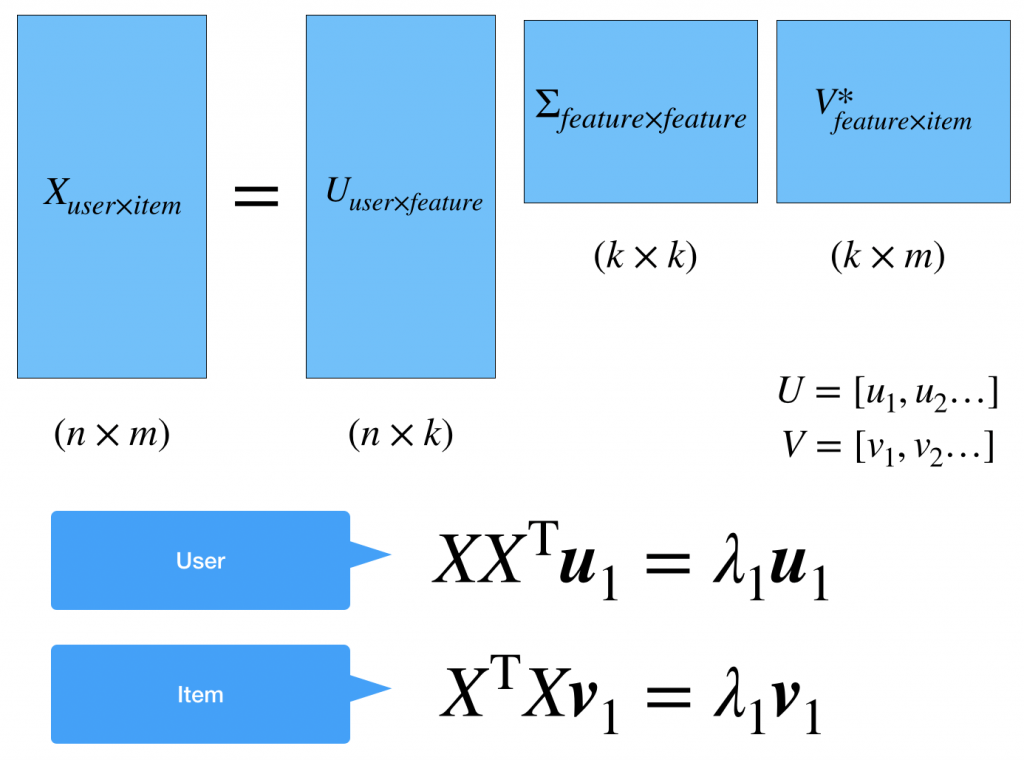
上の図がSVD分解といわれる行列の分解です。PCAの一般化です。なぜなら非正方行列でも分解できるからです。 $X$ がデータの行列になります。これを三つの行列の積に分解します。

まず注目してほしいところは $k$ です。これが潜在的な特徴量の次元になります。特異値と固有値の関係を考えると、固有値が寄与率なら関与することから特異値の最小値が0になるように選べばいいのではないかと個人的に思ってます。解釈についてはたとえば今回の例だとitemはmovieなのでk=genreの数とすれば理解しやすくなるんじゃないかと思ってます。

次に $U$ と $V$ です。これは簡単な計算から固有ベクトルが並ぶことがわかります。これはPCAと同様で重要な軸と捉えればいいと思います。特徴量ベクトルとも言われます。というのはたとえば $U$ の行ベクトルは各ユーザーの特徴を持ったベクトルになるということです。

分解後に行列の積を取ることで未知のratingを計算して映画をレコメンドする手法です。計算については次のmfの方がわかりやすいのでそちらで解説します。ちなみにSVDは自然言語処理でもつかわれます。

ただ、勘のいい人なら気づくと思いますが今回の行列ってかなりスパースなんですよね。SVDはスパースだとよくないらしい。そこで強強のMFが登場するわけです。

Matrix Factorizationを使う作戦

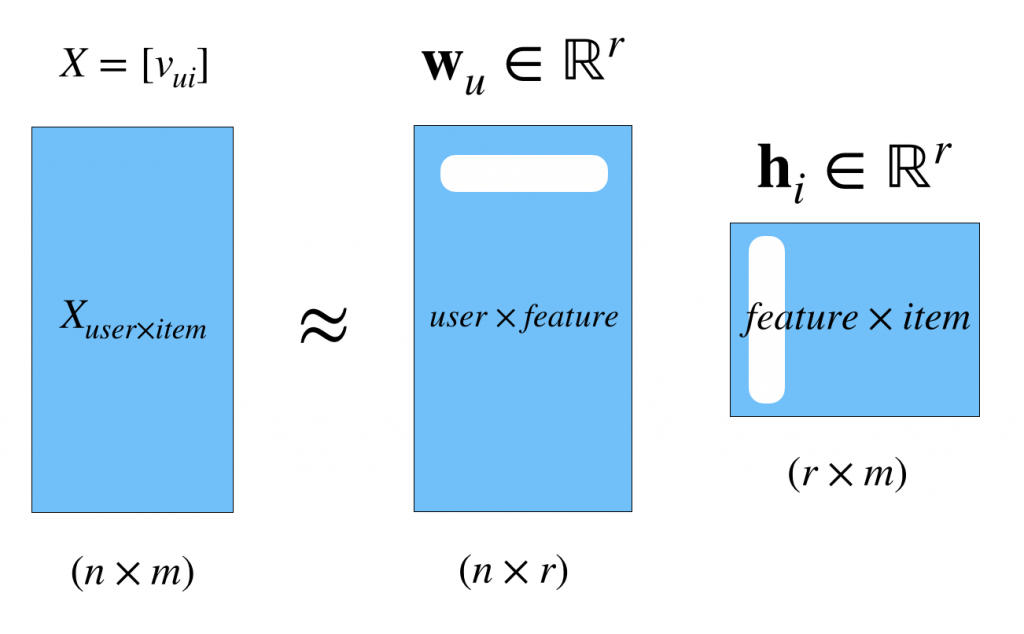
先ほどとは異なり。元の行列Xを二つの行列の積で近似します。この二つの行列がそれぞれユーザー行列、アイテム行列的なイメージです。つまり、画像の白い部分がそれぞれの特徴量ベクトルになります。(SVDと同じです。)たとえばaさんの映画に対する特徴量ベクトルとスターウォーズの特徴量ベクトルの内積をとることでaさんのスターウォーズに対するratingを計算しようということです。ここでの $r$ は先ほどの $k$ と思ってもらえればよくて、つまりジャンルの数的なものです。こちらが指定するハイパーパラメータです。

これはMatrix Factorizationというアルゴリズムですがこれが凄すぎたので解説します。

もともとネットフリックスの映画のレコメンドのコンペがあったようで、その優勝者が提案したアルゴリズムらしいです。

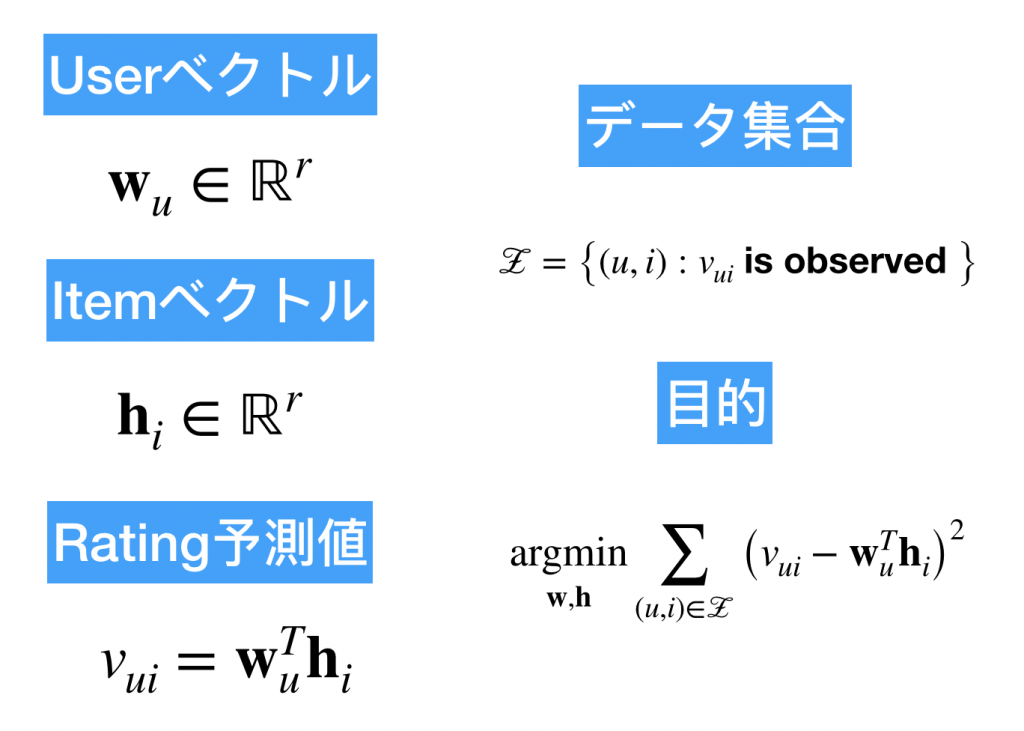
先ほどのSVDはスパースが問題でした、というのは見てない映画はratingは存在しないつまりゼロ埋めですし、見ていても評価していない可能性もあります。しかし、MFはそんな欠損値を無視できます。なぜならば上の図のデータ集合を見てください。observedつまりratingがある要素のみを行列から取り出して学習データにします。

MFのアルゴリズムは単純です。勾配法を使ってユーザー行列、アイテム行列を更新していき、元の行列Xに近似しようというものです。なので上の図で目的がそれぞれの行列の最小化になっています。（ $v_{ui}$ はXのrating成分です。）

で、このままやってもいいんですけど、正規化項を付与しちゃいます。