こんにちは。
本日はついにMCMCです。ベイズ推定とMAP推定がまだの方は次のリンクからどうぞ。
ギブスサンプリングをやっていくんですけど、その前にMCMCについて簡単に説明します。本当に簡単にです。
MCMC
マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods、MCMC) の略であり、求めたい確率分布をマルコフ連鎖を作成することをもとに、確率分布のサンプリングを行うアルゴリズムの総称である。
ここでマルコフ連鎖とは
確率過程の一種であり、未来の挙動が現在
の値だけで決定され、過去の挙動と無関係である(マルコフ性)。各時刻において起こる状態変化(遷移または推移)に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。
難しそうに聞こえますが簡単です。明日の飯が今日の気分だけで決まる感じです。
ちなみにMCと確率遷移行列(マルコフ行列)と呼ばれる物はセットですが、ここでは割愛。でわでわ、気を取り直してMCMCです。
ベイズ推定について述べた際に、![]() の部分が解析的に解けないことがよくあると言いました。たとば多変量になればなるほど積分がシンドくなりますよね。ということで確率分布を直接求めるのではなく、そこからサンプリングして擬似的に求めようというものなんです。
の部分が解析的に解けないことがよくあると言いました。たとば多変量になればなるほど積分がシンドくなりますよね。ということで確率分布を直接求めるのではなく、そこからサンプリングして擬似的に求めようというものなんです。
Gibbs Sampling
で、MCMCの一つであるギブスサンプリングを今回やります。これは確率分布を条件付き確率分布に無理やり分解して一変量ずつサンプリングしようという作戦。もちろん、マルコフ性を仮定してます。
たとえば![]() という2変量の同時分布からサンプリングするよりも
という2変量の同時分布からサンプリングするよりも![]() の方が簡単ですよね。次元が一つ減ってるようなものなので。で、このアルゴリズムはCoordinate descentに似てます。注目する変数以外を固定して計算していくので座標降下法のようにジグザグにサンプリングされます。で、もちろん初期値は適当に選ぶんですけど、バーンインというものがあります。これは初期値から一定時間までの間に得られたサンプルは捨てようという期間です。
の方が簡単ですよね。次元が一つ減ってるようなものなので。で、このアルゴリズムはCoordinate descentに似てます。注目する変数以外を固定して計算していくので座標降下法のようにジグザグにサンプリングされます。で、もちろん初期値は適当に選ぶんですけど、バーンインというものがあります。これは初期値から一定時間までの間に得られたサンプルは捨てようという期間です。
ギブスサンプリングをいきなりベイズ推定で使うのは難しいのでまずは簡単な例でアルゴリズムを理解してからベイズ推定に応用しようと思います。ではいきましょう。
2次元ガウス分布を用いた例
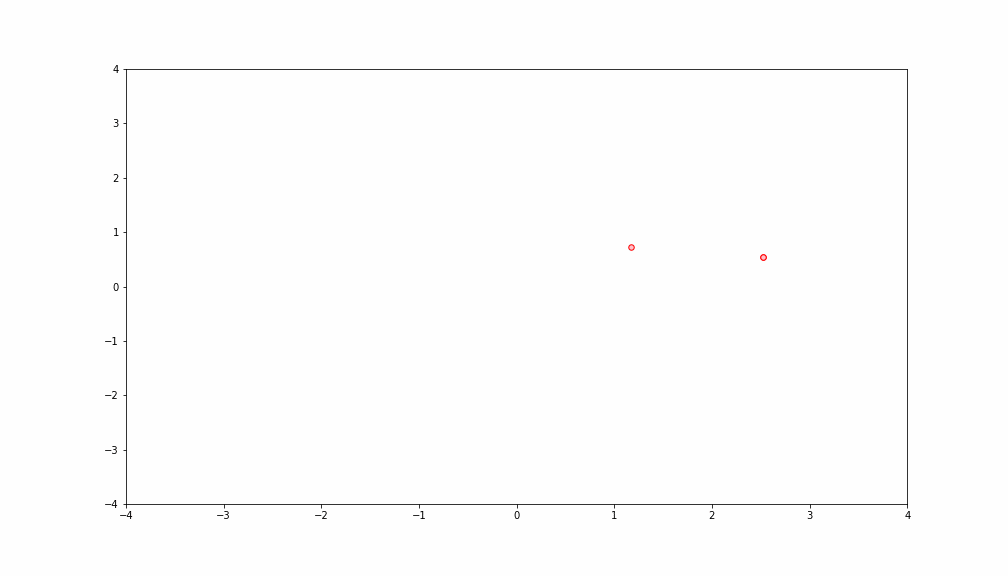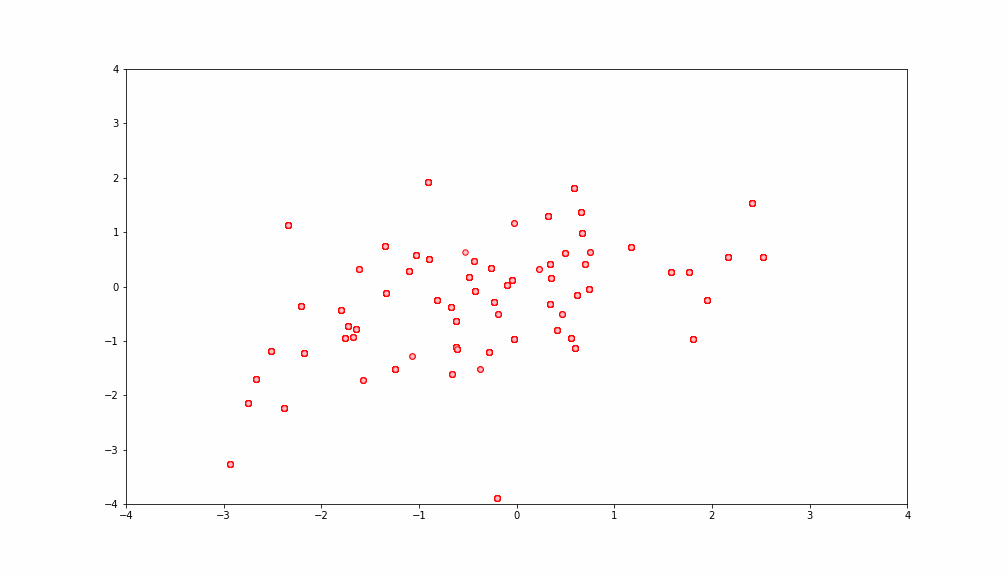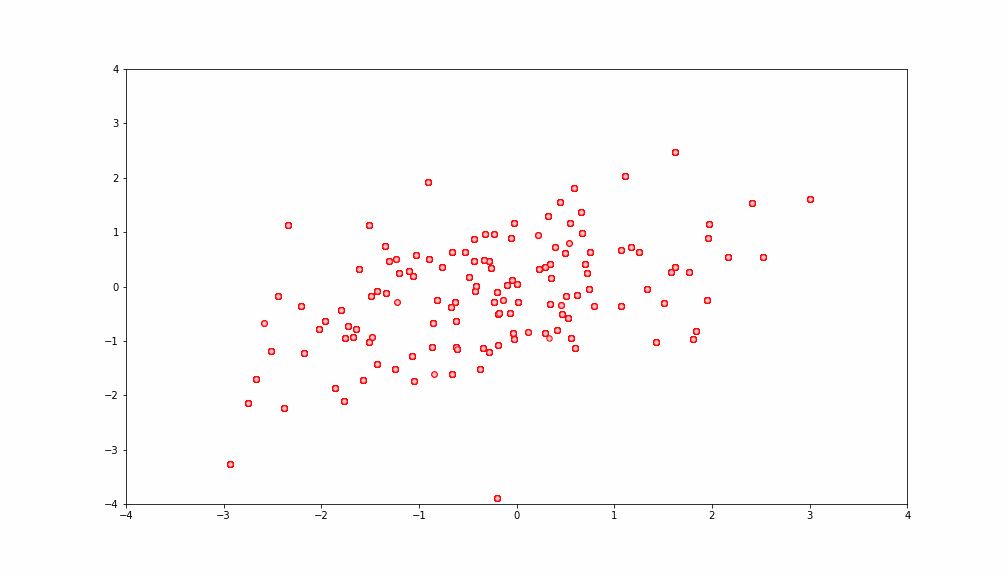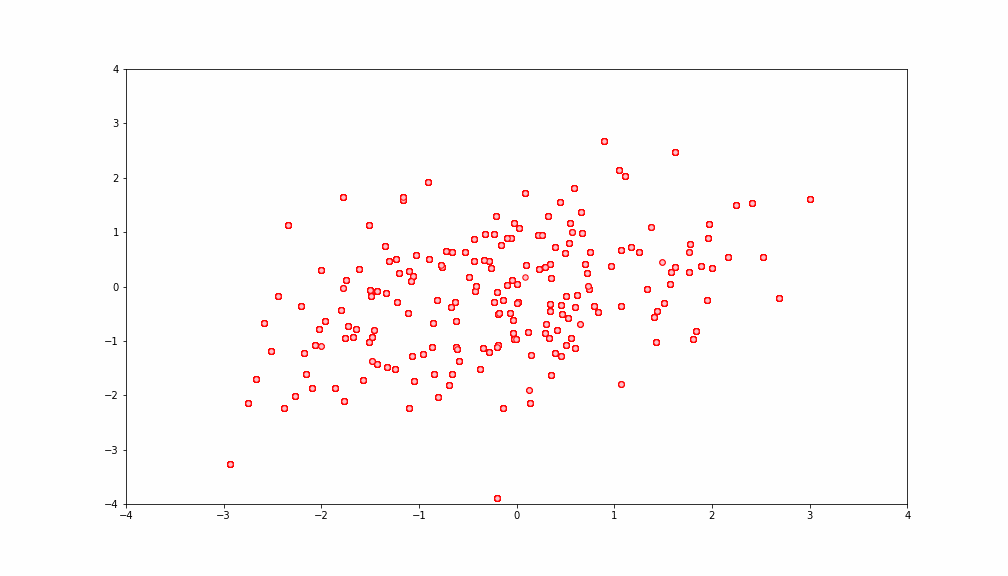
二次元ガウス分布(等高線プロットか3Dプロット)からサンプリングしようと思います。つまり、![]() から点をどんどん取ってくるイメージです。最終的に下を目指します。(赤い点がサンプリングした点)
から点をどんどん取ってくるイメージです。最終的に下を目指します。(赤い点がサンプリングした点)
まずは![]() 次元ガウス分布の式を思い出します。
次元ガウス分布の式を思い出します。
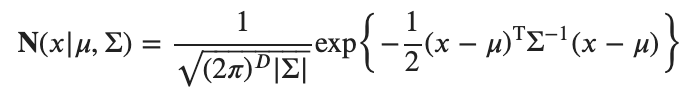
今回は![]() でやります。平均と分散は次のように設定します。
でやります。平均と分散は次のように設定します。
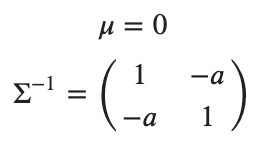
ただし、![]() とします。逆行列と行列式も先に計算しておきます。
とします。逆行列と行列式も先に計算しておきます。
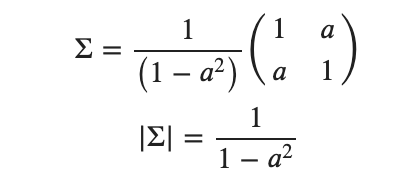
では同時分布![]() をベクトル表記からスカラー表記に書き下します
をベクトル表記からスカラー表記に書き下します
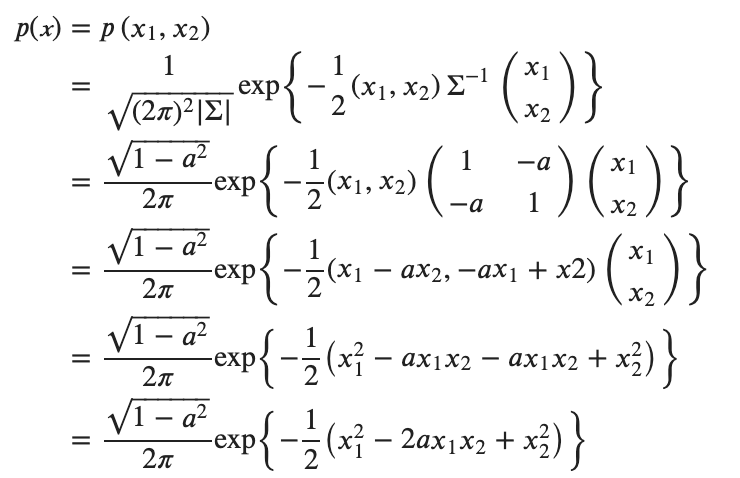
で、目標の条件付き確率は
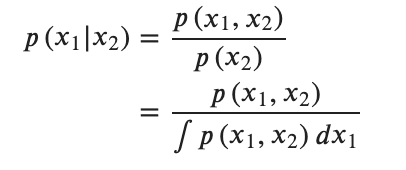
となり、先ほどの式を平方完成すると分母の周辺化が容易になるので
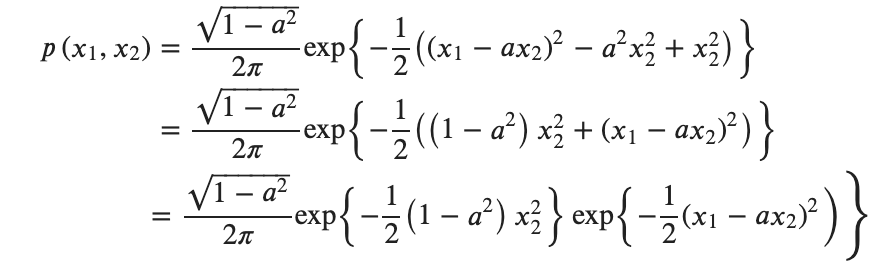
と、平方完成しました。あとはガッツリ積分していって条件付き確率を導出します。「なに分布にしたがうのかなー」と思いながら計算するといいです。
分母の積分をやっていくんですがガウス積分を使います。ガウス積分自体は極座標と重積分でいわゆる![]() 計算で求まるのでここでは割愛します。
計算で求まるのでここでは割愛します。
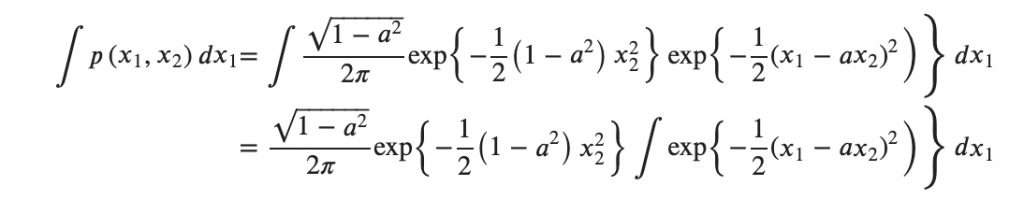
今、![]() 以外は固定しているので定数とみなせます。
以外は固定しているので定数とみなせます。
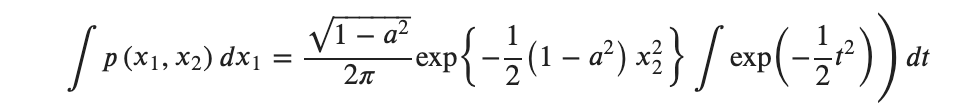
あとはガウス積分を用いて
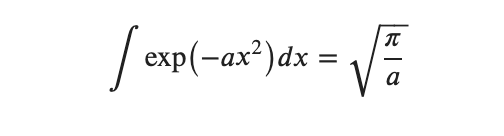
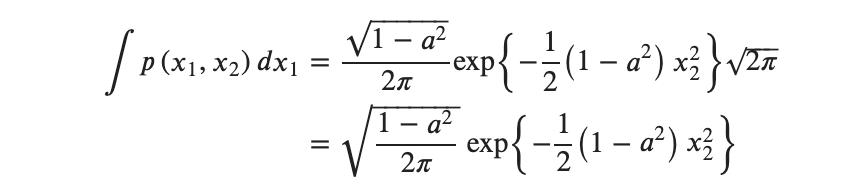
周辺化も計算できたことなので条件付き確率を改めて計算すると
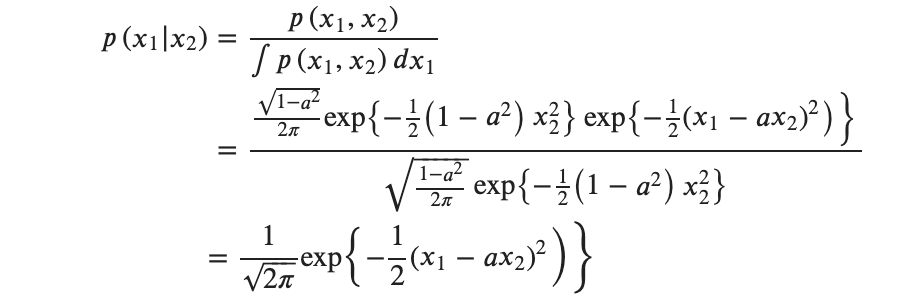
これは![]() の一次元ガウス分布ですね。つまり、正規分布にしたがうことがわかりました。よかったです。これでサンプリングできますね。次元も一つ落ちました。
の一次元ガウス分布ですね。つまり、正規分布にしたがうことがわかりました。よかったです。これでサンプリングできますね。次元も一つ落ちました。
ではコードを書いていく前に。アルゴリズムの流れの確認です。
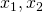 をそれぞれ初期化
をそれぞれ初期化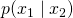 より
より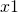 を発生させる
を発生させる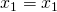 で更新
で更新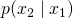 より
より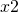 を発生させる
を発生させる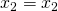 で更新
で更新- 2.〜5.を繰り返す
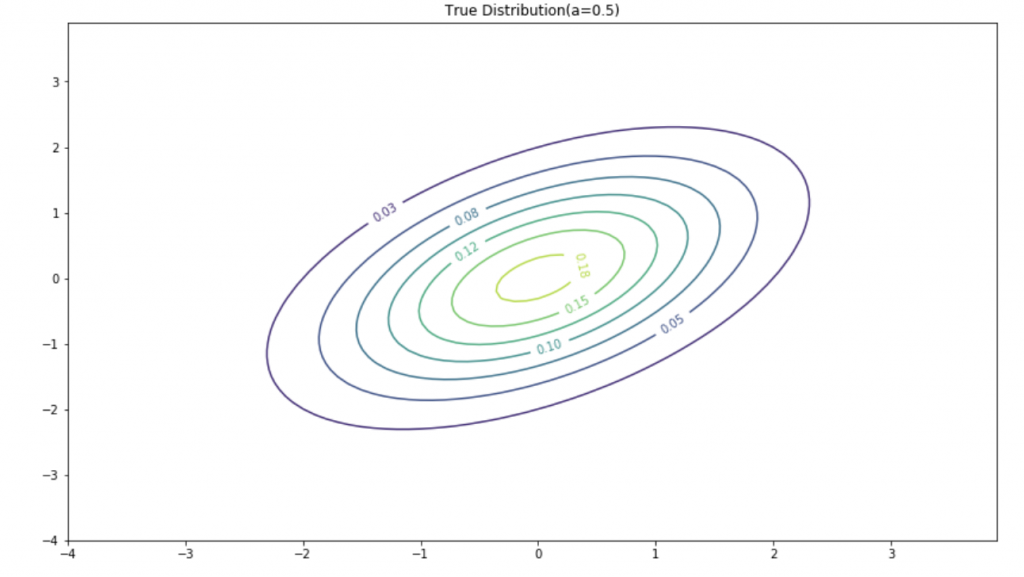
上の真の分布に対してギブスサンプリングで得られたものは
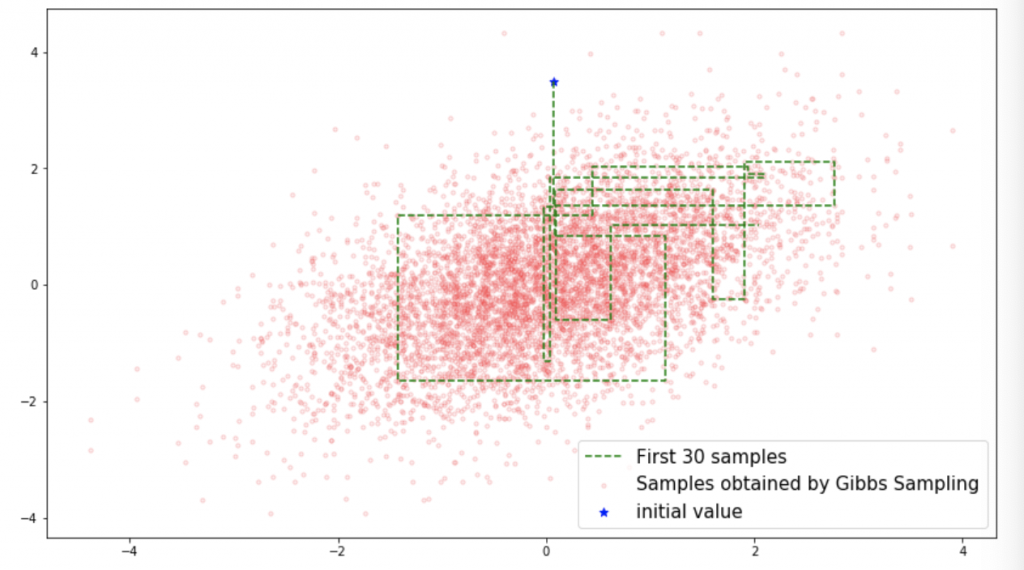
いいかんじですね。今回は平均もゼロですし、シンプルだったので簡単でしたが一般化するともう僕はシンドイです。。。
ベイス推定に応用
ではギブスサンプリングを用いてパラメータの事後分布をサンプリングで得たいと思います。対象となるパラメータは一次元ガウス分布の![]() です。
です。
データ、尤度、事前分布を次のように設定します。
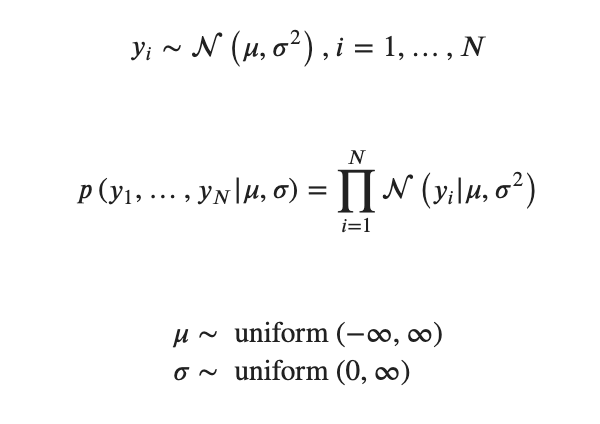
では![]() をサンプリングするための条件付き確率の式を導出します。上の例のように正規分布になってくれるといいなーと思いながら導出します。
をサンプリングするための条件付き確率の式を導出します。上の例のように正規分布になってくれるといいなーと思いながら導出します。
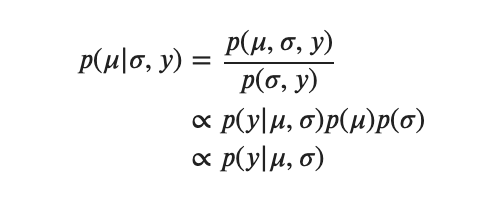
分母は関係ないので消し去りました。では![]() に注目して計算します
に注目して計算します
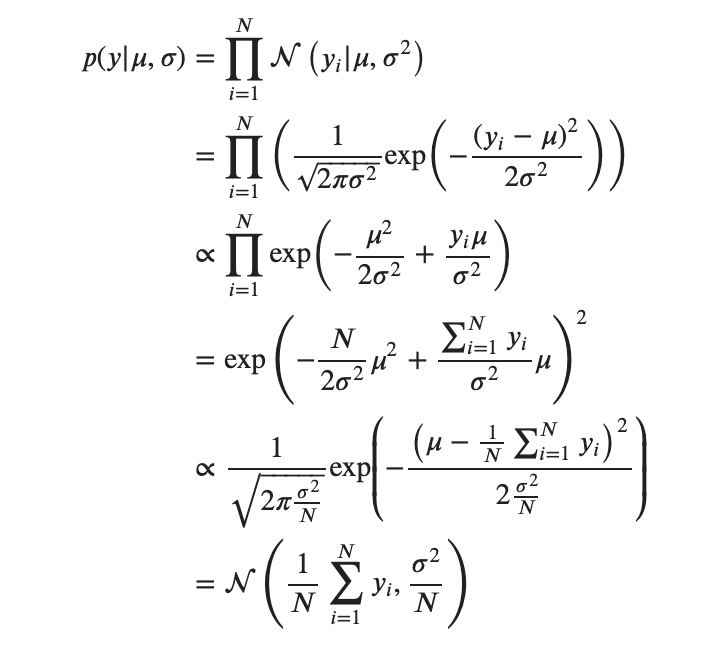
よかったです。正規分布になりました。(4行目から5行目にかけては![]() についての平方完成)
についての平方完成)
このノリで![]() をサンプリングするための条件付き確率の式を導出します。何度も言いますがどんな分布になるか想像しながら計算します。
をサンプリングするための条件付き確率の式を導出します。何度も言いますがどんな分布になるか想像しながら計算します。
先ほどと異なり、注目すべき変数は![]() です。となるとですね、
です。となるとですね、
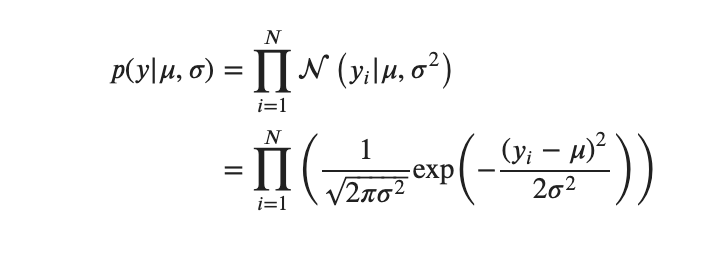
ここから例えば![]() では平方完成できないですよね。となると正規分布には間違いなく従わないでしょう。んーーー、困った。
では平方完成できないですよね。となると正規分布には間違いなく従わないでしょう。んーーー、困った。
んーーーーーーーーーーー、と悩んでいても仕方ないので対数をとってみましょう。
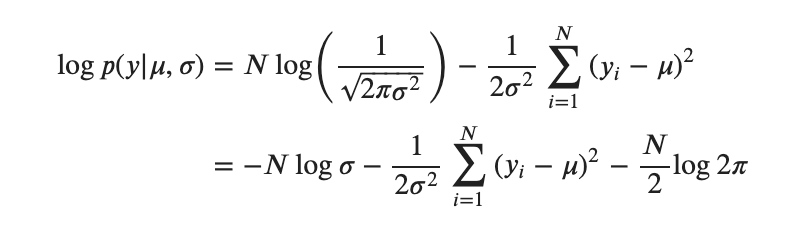
ふむふむ、全くわからないです。僕は閃かなかったのですがガンマ関数がヒントになるらしいです。
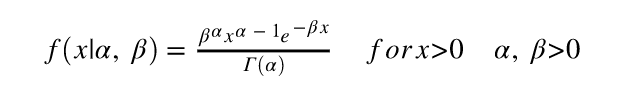
とりあえず分母を無視して
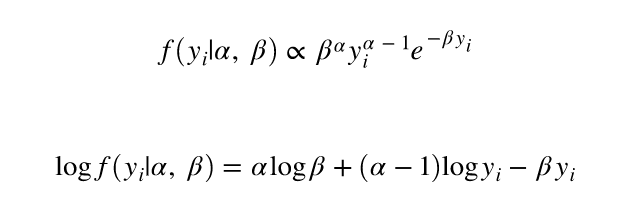
ここで必殺技です。先ほど「んーーー」と止まった式を![]() と置き換えると(このタウは精度と呼ばれる)
と置き換えると(このタウは精度と呼ばれる)
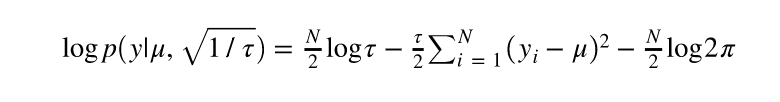
となって、![]() に注目すると以下がわかりました。
に注目すると以下がわかりました。
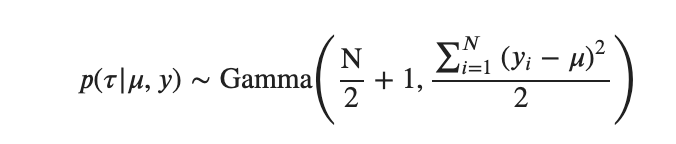
これすごいですよね、対数の式から分布を決定するなんてめっちゃ賢くないですか?まあこれをコードでかいてやってみると
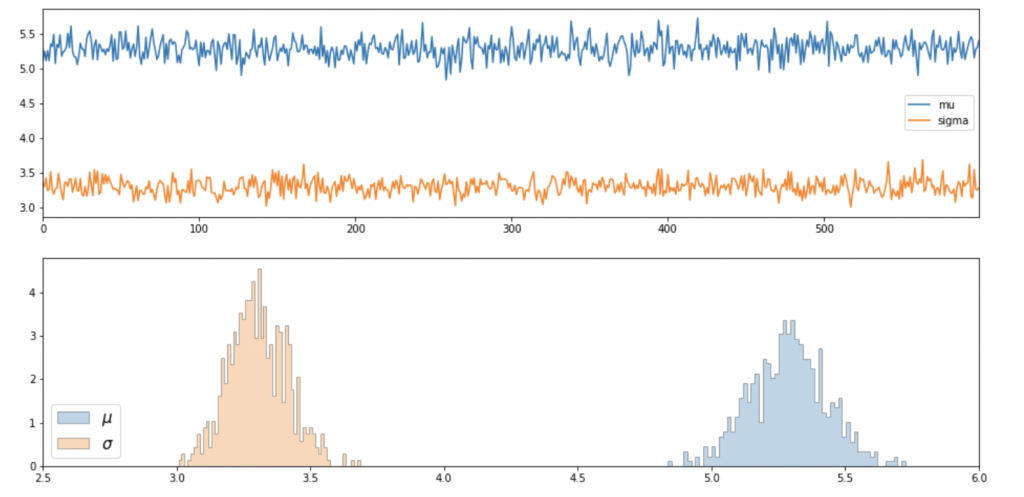
うまくいったようです。よかったよかった。ただnumpyのガンマ関数のパラメータが逆数になっていることに注意してください。詳しくはコードにリンク貼ってます。
疲れましたあ。これ簡単な例だったからよかったですけど実際自分で全部モデリングしたらしんどそうですね、例えばパラメータが2から4になったら、、、、、もう眠れません。でわ
Reference
- http://kazufusa1484.hatenablog.com/entry/2017/06/21/133348
- https://github.com/jojonki/gibbs-sampling