こんにちは。

前回、MAP推定までやりました。

しかしプロットもコードも書かなかったのでMAP推定をプロットするところからはじめます。復習がてらにね

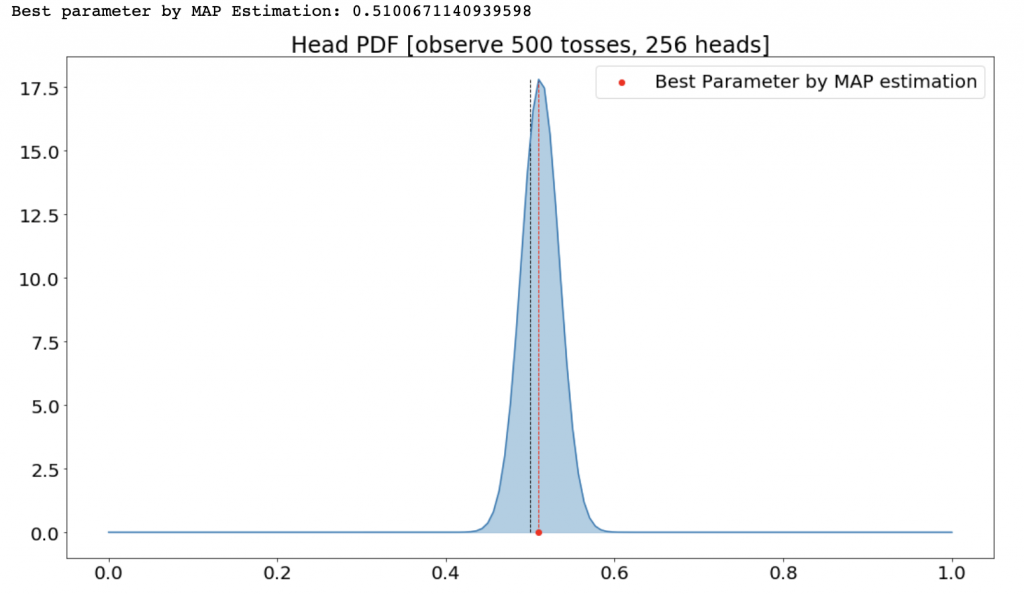
この青いプロットは今回のテーマであるベイズ推定です。まぁそれは置いておいて、「尤度x事前分布」の最大化がMAP推定でした。プロットすると上図のように山が最も高くなる点になります。

MAP推定とベイズ推定の違いを簡単に

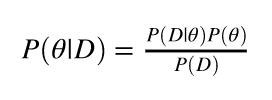
MAP推定は右辺の分子の最大化でした。一方でベイズ推定とは分母を切り捨てずちゃんと計算して左辺をちゃんと導出します。（なぜ切り捨ててよかったというとP(D)はパラメータ\thetaに依存しないからです。）

ということはベイズの方が難しいんですよ。（ちなみに最尤法、MAP推定は値を推定するので点推定とも呼ばれます。）

なぜベイズ推定したいのか？

これはあくまで僕なりの理解と見解なのでそれを踏まえて聞いて欲しいです。

前述通りMAP推定よりベイズ推定の方が難しいです。理由は分母の計算があるからです。この計算は積分の形になり、さらにいうと計算できなくて困っているくらいなのです（MCMCとかで対応）そこまでしてベイズ推定するメリットはなんなのか？なぜMAP推定ではダメなのか？

僕の理解だとまず、MAPがダメというわけではないです。ベイズ推定の結果がMAP推定と同値的なことになることはあります。

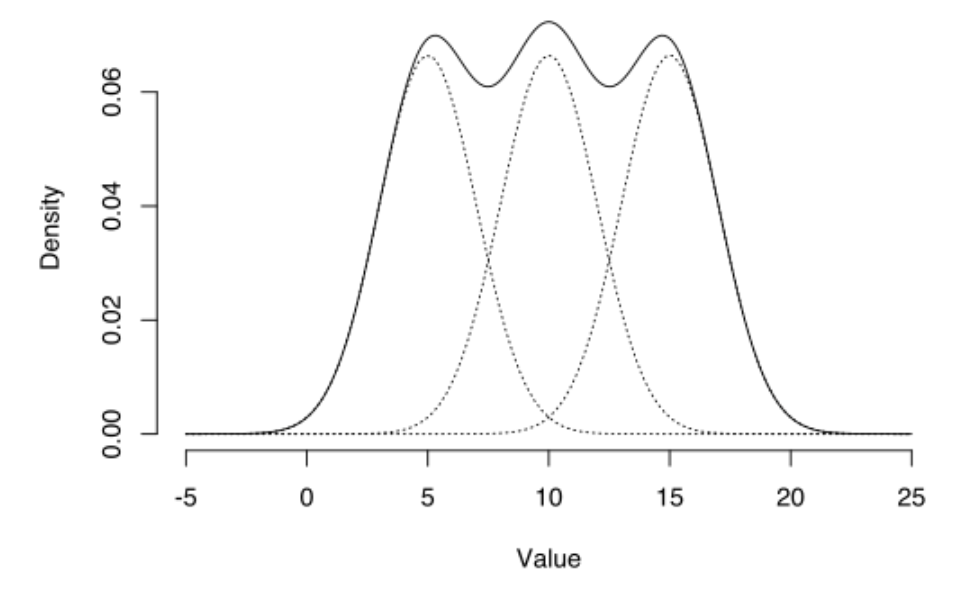
例えばベイズ推定後のパラメータの分布が上のようになったとしましょう。するとベイズ推定最大の利点の一つは「平均をとることもできる」という点だと思っています。説明すると、MAP推定のみの場合は得られる情報は真ん中の山の頂点を指す点、つまり\theta=10のみです。

一方で、ベイズ推定をすると事後分布の全体像がわかるため、例えば図においていい山が３つあるので平均をとって

    \[ \theta=\frac{6+10+17}{3}=11\]

のようにパラメータをより主観的に微調整できるのです。なぜ主観的という言葉を使ったかというとそもそもベイズの根幹に

直感・主観

を反映させるというアイデアがあるからです。

ベイズ推定

最も簡単なのでコイン投げを例に取りましょう。なぜ簡単かというとパラメータが一つで済むからです。というのは表が出る確率を\thetaとすると自動的に裏が出る確率が1-\thetaということです。

加えて計算も楽なのです。（僕は数学が苦手なので複雑な理論とかはできない。）ここではパラメータ\thetaの分布をベイズ推定で求めると同時に、その分布の変化を可視化することで理解を深めます。

パラメータの確率密度関数をf_n、コイン投げの結果x_nをH(head)、T(tale)で表し、確率変数をcと表すことにします。

例えば

    \[f_n(\theta) = f_n(\theta|c=H)\]

は表が出た時のベイズ推定で得た分布ということです。これを踏まえるとn+1回目の更新では次のようになります。

    \[f_{n+1}(\theta) = f_{n+1}(\theta|c=x_n) = \frac{p(c=x_n|\theta) f_n(\theta)}{p(c=x_n)} \]

ただし

    \[ p(c=x_n) = \int_0^1 p(c=x_n|\theta)f_n(\theta) d\theta \]

では事前分布を決めましょう。これは上式のf_1に相当します。事前分布とはパラメータに仮定する分布でした。今回のパラメータ\thetaはコインが表をだす確率です。僕なら事前分布に一様分布を仮定します。なぜなら表も裏も同じくらい出るだろうと思っているからです。

え？一様分布はいや？なら例えば次のような例を考えてみましょう。コイン持っていた人間が表がめっちゃ好きな人間なら事前分布は右に偏ったものになりますよね。つまり一様分布とはかけ離れ\theta=1付近で最大値をとるようないわばデルタ分布とかを仮定することになります。しかし、話がややこしくなるんです。なので一様分布で許してください。

つまり

    \[ f_1(\theta) = 1 \]


前回の記事を読んでくれた方は共役事前分布は？と思ったかもしれないがいったん忘れてください。なぜならとことん話が簡単になるからですよ。

残るは尤度、上式のp(c=x_n)のみです。尤度とはなんだった？それは試行の結果をパラメータを用いて表現したモデルでした

つまり、x_1=Hだったとするとその事象に対する尤度は

    \[ p(c=H|\theta) = \theta \]

となります、実にシンプルだろ？もし二項分布とかでやると計算がうわああってなります。（サイコロのようによりマルチなものをやろうとするとディリクレ分布とかが絡んできて、うわあああってなります）

ではベイズ推定してみよう。前述通りx_1=Hというデータが得られたとします。まずは分母つまり次の積分を計算しましょう。

    \[ p(c=x_1) = \int_0^1 p(c=H|\theta)f_n(\theta) d\theta \]

代入すると

    \[ p(c=x_1) = \int_0^1 \left( \theta \times 1 \right) d\theta = \frac{1}{2} \]

では分子も計算します

    \[f_{2}(\theta) = f_{2}(\theta|c=x_1) = \frac{p(c=H|\theta) f_1(\theta)}{1/2} \]

    \[f_{2}(\theta) = \frac{ \theta \times 1}{1/2} = 2\theta \]

もとまりました。少しまとめてみましょうか。

  1. （試行前）裏表同じくらいで出るよなー？
  2. （試行）Headが出た
  3. （試行後）まじ？まさか表出やすい？けどゆうてまだ一回目やしな

今この3にいるわけです。ではもう一度ベイズ推定してみましょう。
f_2はx_2というデータを用いたベイズ推定における事前分布となることに注意します。

二回目の試行も一回目と同じくx_2=Hだったとします。すると尤度は

    \[ p(c=H|\theta) \]

なのでこれを用いて先ほどと同様に積分と分布を計算します

    \[ p(c=x_2) = \int_0^1 \left( \theta \times f_2(\theta) \right) d\theta = \frac{2}{3} \]

    \[f_{3}(\theta) = f_{3}(\theta|c=x_2) = \frac{p(c=H|\theta) f_2(\theta)}{2/3} \]

    \[f_{3}(\theta) = \frac{ \theta \times 2\theta}{2/3} = 3\theta^2 \]

となりました。先ほど同様にまとめます。

  1. （試行前）裏表同じくらいで出るよなー？
  2. （試行）Headが出た
  3. （試行後）まじ？まさか表出やすい？けどゆうてまだ一回目やしな
  4. （試行）Headが出た
  5. （試行後）うせやろ？これ表しかでーへんパターンやろ

こんな気持ちですよね。この気持ちが分布（密度関数f_n）として現れているんです。というのはf_nに注目してみると

  1. f_1 = 1
  2. f_2 = 2\theta
  3. f_3 = 3\theta^2

とこれ単調増加具合が増えてますよね。可視化してみます。

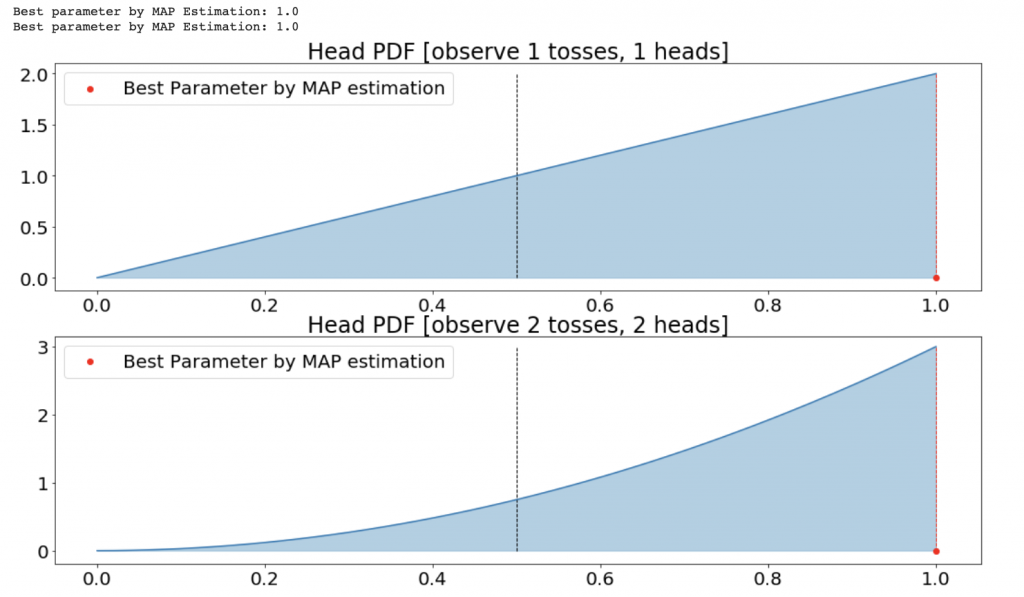
まとめますとベイズ推定で得られる事後分布とはデータを知った後のパラメータに対する気持ちの分布なのです。今の例だと二回も連続で表が出たので表の出る確率が1に近いほど確率密度が高いのです。

もっとシュミレーションすると

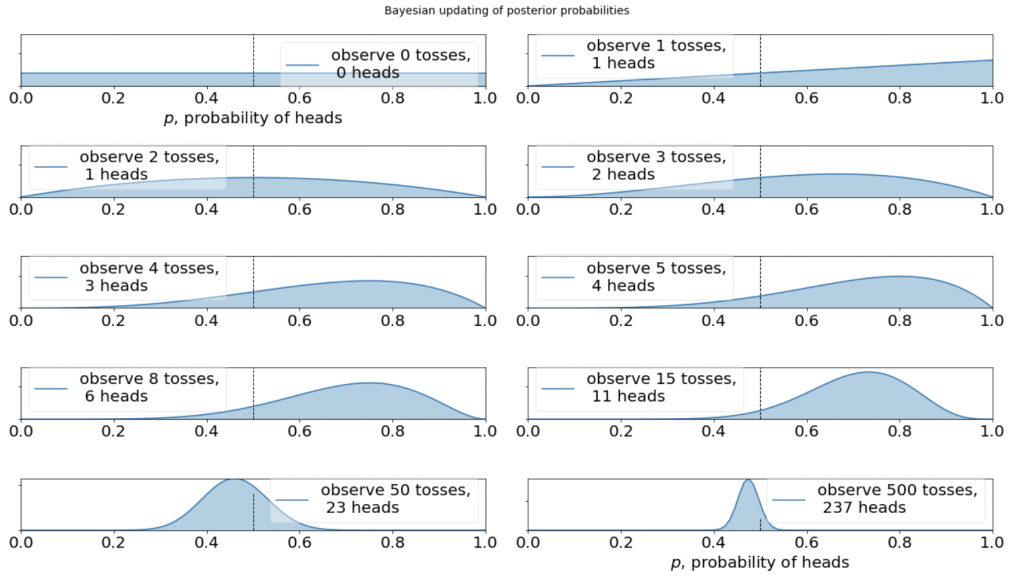
ディリクレ分布でもやりたいんですけど、もう計算が酷くて、、、それよりmcmcしたいですよね。数値計算で積分求めるなんて素敵だと思いませんか？でわ