こんにちは。kzです。
今まで数学に触れつつ機械学習を中心に書いてきましたが、おそらく読者さんは数学科の方ではないと思うのでアルゴリズムの記事をみて、数学書を読もうとした方が本を買ってから後悔しないように、大学一年で習う集合論というものを簡単にまとめてみました。なのでこれは素人の方が数学書の初戦でボコボコにされないための踏み台のような扱いになればいいかな、と思っています。なお、この内容は大学の数学科1年生が習うものになります。
集合
数学で考える対象のはっきりとした集まりのことを集合といいます。ある集合
有限個の元からなる集合を有限集合と呼び、無限個の元からなる集合を無限集合と呼びます。
集合を表す場合、
自然数全体の集合などに以下の記号を用います。
 自然数全体の集合
自然数全体の集合 整数全体の集合
整数全体の集合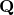 有理数全体の集合
有理数全体の集合 実数全体の集合
実数全体の集合 複素数全体の集合
複素数全体の集合
空集合は任意の集合の部分集合であると定義します。
集合
有限個の集合
ここまでは高校数学でも経験があると思うので直積を除いて簡単ですね。直積は書き方が独特ですが、ただの写像です。簡単にいうと、「二倍する」という写像は引数をひとつ取り出力をひとつ返します。一方で「掛け算」という写像は二つの引数に対しひとつの出力を返します。このようにいくつかの引数を考えるときに直積を使います。
写像
集合また、
2つの写像
「写像」という言葉が出てきましたがただの「関数」だと思ってもらって構いません。人によっては「作用素」と言う人もいます。「
Proposition
- 3つの写像
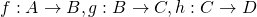 に対して等式
に対して等式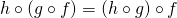 が成り立つ.
が成り立つ.
Definition
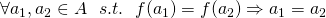 が成り立つとき
が成り立つとき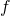 は単射であるという
は単射であるという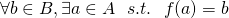 が成り立つとき
が成り立つとき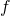 は全射であるという
は全射であるという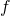 が単射かつ全射であるとき、
が単射かつ全射であるとき、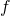 は全単射であるという
は全単射であるという
写像
「逆写像」とよく間違えられるもので「逆像」と言うものがあります。また、「恒等写像」が出てきましたがこちらは有名なResnetのアルゴリズムで登場します。
Proposition
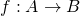 が逆写像を持つことと
が逆写像を持つことと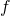 が全単射であることは同値である
が全単射であることは同値である
関係
Definition
- 任意の
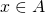 に対して
に対して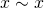 (反射律)
(反射律) 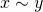 となる任意の
となる任意の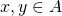 に対して
に対して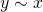 (対称律)
(対称律)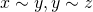 となる任意の
となる任意の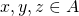 に対して
に対して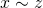 (推移律)
(推移律)
「同値類」、「商集合」は初見で理解するのは難しいものだと思います。僕のイメージとしてはとある集合に対して「グルーピング」の動作を考えます。ここでグルーピングされてできた新たな集合を商集合、各グループを同値類、グルーピング方法を同値関係と言います。簡単な例は割り算のあまりです。
Definition
- 任意の
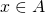 に対して
に対して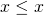 (反射律)
(反射律) 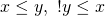 となる任意の
となる任意の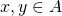 に対して
に対して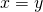 (反対称律)
(反対称律)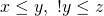 となる任意の
となる任意の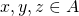 に対して
に対して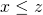 (推移律)
(推移律)
順序集合
このとき、
任意の全順序部分集合が上界を持つような順序集合を帰納的順序集合といいます。また、
順序集合に関しては記号のせいか混乱する友人が多いです。あくまでただの記号なので大小を図る記号の存在は一旦忘れてください。
多様体シリーズとかも欲しいですか?でわ。