ロジスティック回帰を数式から

2019.07.27

機械学習

こんにちは。

本日はロジスティック回帰の実装をやっていこうと思います。といっても非常に簡単なニューラルネットなのでやらなくてもいいかなと思ったのですが、いきなりSoftmaxを実装するのもアレなのでまずは簡単なこちらからやっていこうと思います。

ロジスティック回帰とは？

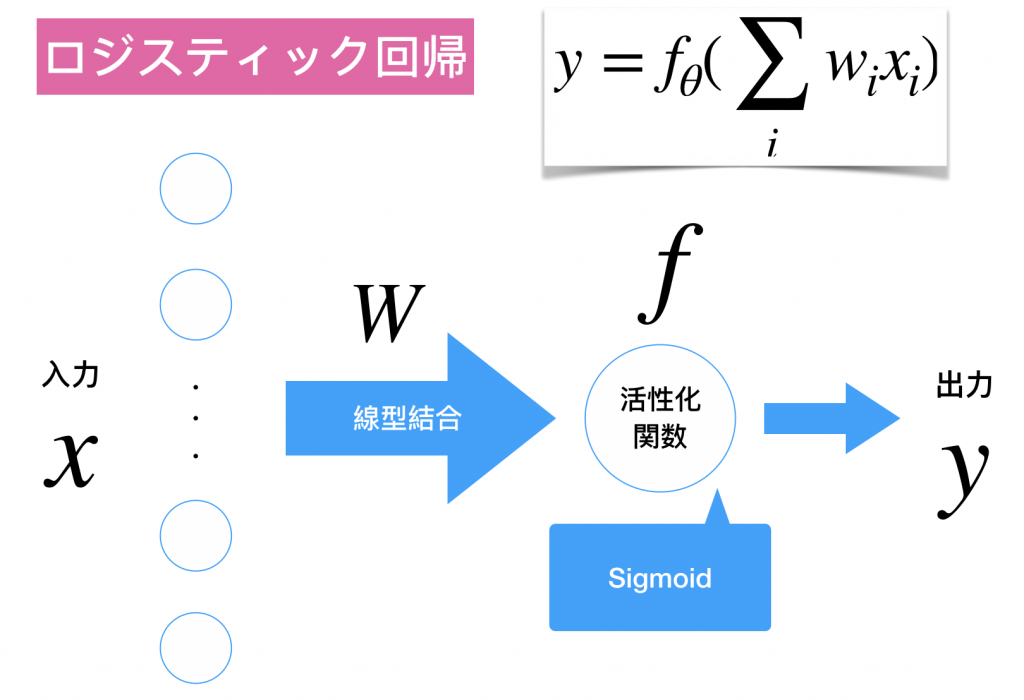
教師あり学習、２値分類を確率の出力で行います。具体的には閾値を自分で設けます。ロジスティックの場合は0.5だと思います。つまり、シグモイドの出力に対してが0.5以上ならラベル１、0.5未満ならラベル２を振り与えて２値分類を行うわけです。また、これを多値分類に拡張したものがソフトマックスになります。

数式導出

まずはシグモイド関数について

$\phi(z) = \frac{1}{ 1 + \mathrm{e}^{-z} }$

微分は

$\frac{d \phi(z)}{dz} = \frac{d}{dz}\frac{1}{ 1 + \mathrm{e}^{-z} }$

$= \frac{ \mathrm{e}^{-z} }{ (1 + \mathrm{e}^{-z})^2 } = \frac{1}{(1 + \mathrm{e}^{-z})}( 1 - \frac{1}{(1 + \mathrm{e}^{-z})}) = \phi(z)( 1 - \phi(z))$

でした、これを用います。

今回の目的関数は以下のようになります。

$\sum_{i = 1}^{m}\left ( y_i \log\phi_i + (1 - y_i)\log(1 - \phi_i) \right)$

なぜこうなるかといいますと、尤度関数にベルヌーイを用いるからです。 $\phi_i$ が確率である出力、 $y_i$ が2値（0,1）つまりラベルの値です。

$Likelihood = \prod_{i=1}^{N} \phi_{i}^{y_{i}}\left(1-\phi_{i}\right)^{\left(1-y_{i}\right)}$

あとは対数をとってマイナスを付与しただけです。そしていつものごとく微分していきます。今回の重みは線型結合時に用いた $w_j$ なのでチェーンルールを用いて( $zは線型結合の値です$ )

$\frac{\partial J(w)}{\partial w_j} = \frac{\partial}{\partial w_j} - \sum_{i = 1}^{N}[y_i \log\phi_i + (1 - y_i)\log(1 - \phi_i)]$

$= - \sum_{i = 1}^{N}[y_i\frac{\partial\log\phi_i}{\partial\phi_i}\frac{\partial\phi_i}{\partial z_i}\frac{\partial z_i}{\partial w_j} + (1 - y_i)\frac{\partial\log(1 - \phi_i)}{\partial\phi_i}\frac{\partial\phi_i}{\partial z_i}\frac{\partial z_i}{\partial w_j}]$