こんにちは。
以前、ニュートン法について述べましたが1次元でした。やっぱり多次元じゃないとあんまりスキルアップにならないですよね。ということでやります。ちなみに
差分法を使います。しかし、この記事で初めてニュートン法を知る人のためにも簡単にアルゴリズムを説明してから実装へ移りましょう。
上のリンクがヒジョーーーーにわかりやすいです。では、始めましょう。
結局はこれ、テイラー展開
テイラー展開は非常に便利です。本日もいつものように勾配法を使うのですが、結局局所的にしか関数は見ないんです。「局所的に」というキーワードが来れば「テイラー展開」と覚えましょう。そして一般的にテイラー展開は2次の項まで使われます。すなはち、
![Rendered by QuickLaTeX.com \[ f\left(x_{k}+ x\right) \approx f\left(x_{k}\right)+\nabla f\left(x_{k}\right)^{T} x+\frac{1}{2} x^{T} H(x_{k}) x\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-e9afafc5cfedf650633136fe8821318d_l3.png)
上のは多変数関数
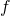
を
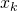
周りでテイラー展開し、二次の項までで近似したものです。ここで
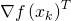
を勾配、
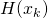
をヘッセ行列と言います。ヘッセ行列の定義は簡単です。
微分を並べるだけです。ちなみに、一変数の場合は次のようになります。
![Rendered by QuickLaTeX.com \[H(f) = \nabla^2 f(x) = f''(x)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-41b633d38bd1070cebcd7b513c0f6b61_l3.png)
ニュートン法について
ではニュートン法ですが、まず正定値行列を知る必要があります。正定値行列とは
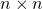 行列
行列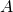 が正定値とは、
が正定値とは、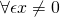 に対して
に対して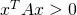 となること。
となること。
なぜこれが重要かというと、極値判定に使うからです。つまり、正定値であれば極小値、負定値であれば極大値です。覚え方は単純、ヘッセ行列は2回微分なので単純に「微分増加率が正か負か」で覚えましょう。極大値であれば「負」になりますね。そしてお待ちかねの更新式は非常にシンプルです。
![Rendered by QuickLaTeX.com \[ x^{t}=x^{t}-\left(\nabla^{2} f\left(x^{t}\right)\right)^{-1} \times \nabla f\left(x^{t}\right)^{T}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-658c61d89e418b81231d9c1e2c2849b5_l3.png)
ヘッセの逆行列をとるので、正則でなければこのアルゴリズムは「THE END」です。加えて、変数の数が多いと逆行列計算がヤバくなって破綻します。一方で、シンプルな勾配法よりも収束が早いことが知られています。では今回の問題を考えます。
ニュートン法 with 差分法
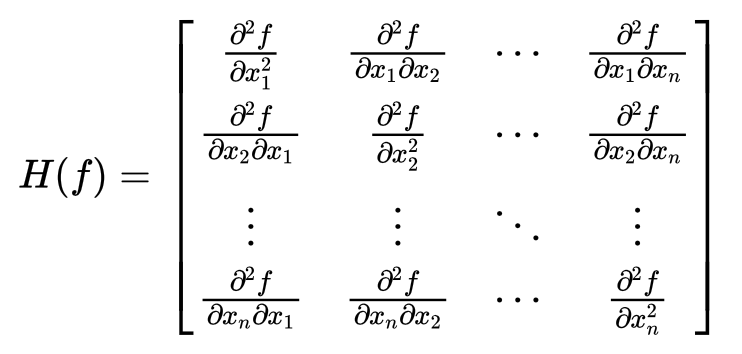
今回の問題はちょっと複雑です。
見ての通り少し複雑です。他のブログで紹介されているニュートン法はシンプルであり、結果的にベクトルとして書き換え直接勾配やヘッセ行列が計算できるようになっていますがこれは見ての通り厳しい。そこで差分法により解決します。差分法を覚えてますか?微分の定義式を使って数値計算により偏微分を計算します。今回の最適化問題は嬉しいことにcontinuousな関数なので偏微分の順序交換が可能です。すなはち
![Rendered by QuickLaTeX.com \[f_{xy} = f_{yx}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-007d5980f339c502507dd89990d87663_l3.png)
です。なぜこんなことを気にするかというと今回は二変数のヘッセ行列を求めるのでこれらをそれぞれ計算する必要があります。さらに前述通り差分法を用いた数値計算です。少しでも工夫するためにはこの等式を活用する必要があります。ヘッセ行列の定義式より
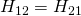
が言えるので計算が1つ減りました、わーい。ではコードに移りましょう。
実装
2種類の初期値を使っています。片方は極小値に行っていないことがわかります。これは初期値が極小値に近くないことが原因です、つまり、ニュートン法はいつでも便利というわけではないということです。
![]()
![]()
行列
が正定値とは、
に対して
となること。
![]()
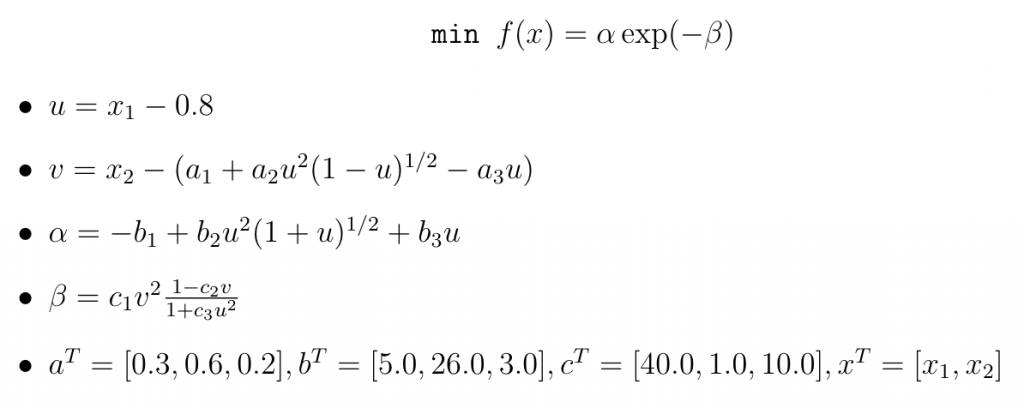
![]()