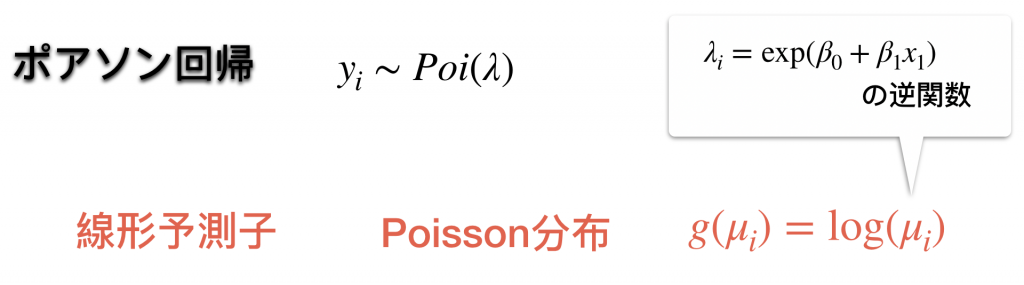こんにちは。
今回はたまに聞くであろうGLM、すなわち、一般化線形回帰についてです。回帰といえば今まで線形回帰とかちょろっとやりました。せっかくなので回帰についてちょっとだけ復習してから本題に入りましょう。
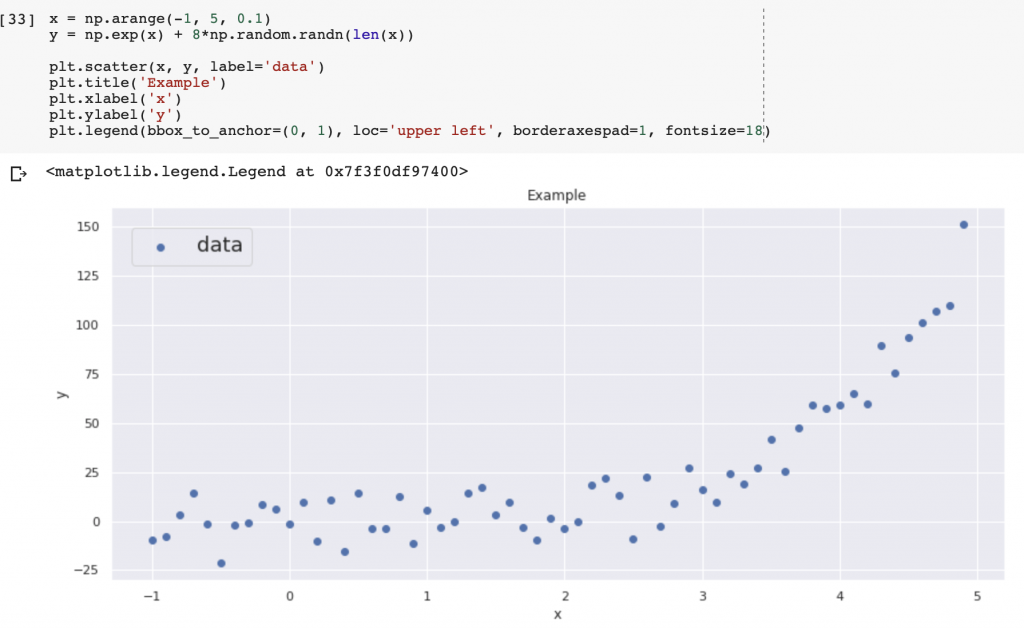
上のデータを回帰することを考えます。今まで線形回帰ばかりしてきました。しかし、今回のデータは線形っぽくない。このような時はどうすればいいのか?一般化線形モデルの登場です。
- データが線形ではないとき
- 誤差が
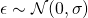 でない
でない  がカテゴリカルとかだったら
がカテゴリカルとかだったら
上記のような場合、線形回帰よりも一般化線形回帰が有効です。一般化線形モデルに入る前に単回帰、重回帰についてもついでに復習しておきましょう。
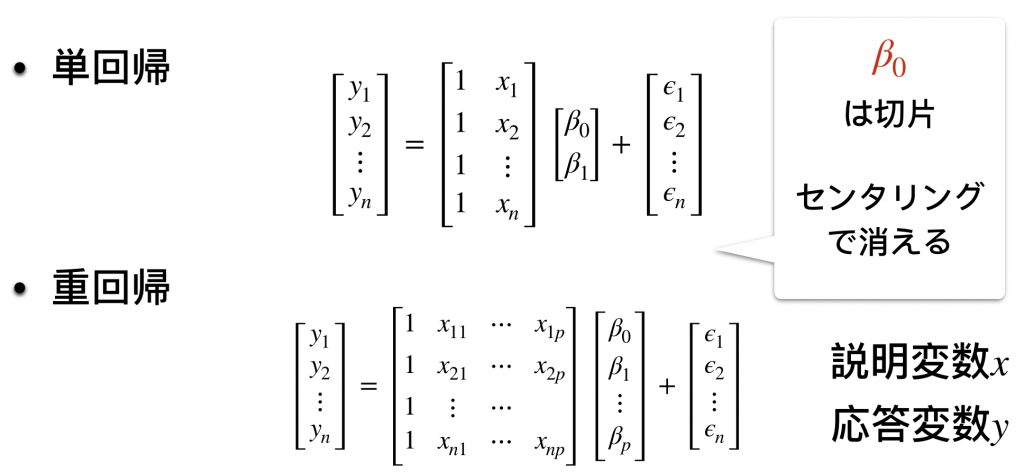
まあ、簡単ですね。では一般化線形モデルへ。

GLMでは上記の3つのファクターが重要になります。これらによりモデルが決まります。
それぞれ、
- 説明変数の線形モデル
- 線形モデルに移す関数
- 目的変数の従う分布
になります。具体的に例を見ていきましょう。

普通の線形モデルは上のようになります。これだけだとわからないのでポアソン分布を例にとってみましょう。
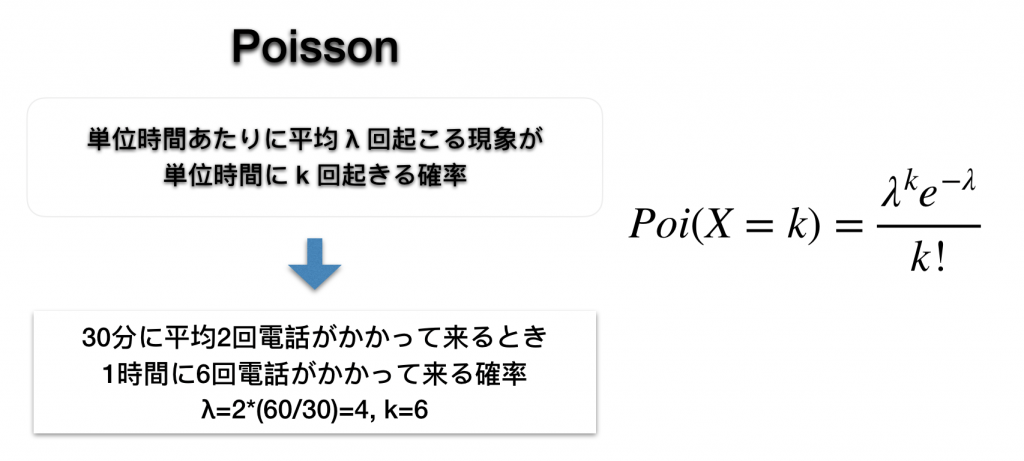
目的変数が非負ということが1つの特徴でしょう。
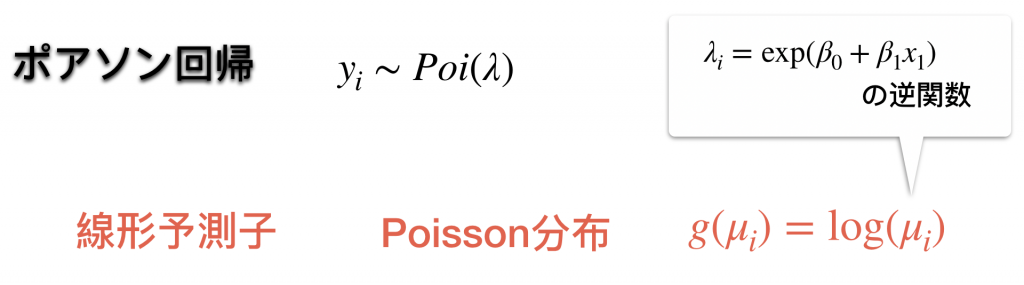
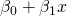
を
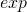
に食わせることで指数関数を用いてモデルを構成しています。線形予測子を得るためには
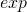
を外せばいいので
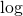
つまり対数がリンク関数になることがわかります。言い換えれば、
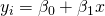
と単純にモデリングしてしまうと目的変数が正規分布に従わないせいで誤差が大きくなってしまいます。それを避けるためにリンク関数により
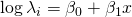
と変形していわば補正をかけます。(
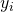
が平均
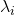
に従うポアソン分布から生成されたと仮定します)
これを用いようとするとPythonよりもRがメジャーな選択肢になりますが、僕はPython派なのでこっちを使います。以下がコードになります。
北大のレジュメの問題はRで解かれておりこれをPythonで解いた結果近い値が得られたのでうまく回帰できたと思います。しかしもう世の中はニューラルネットワークなのか、、、、
でわ

 でない
でない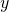 がカテゴリカルとかだったら
がカテゴリカルとかだったら