こんにちは。
久しぶりの投稿になりました。本日の内容はタイトル通りです。
線形回帰とかの目的関数って最適解を持ちましたね。
しかし、ニューラルネットワークはそうはいかないと言いました。
つまり、目的関数が凸関数ではない可能性が非常に高いんですね。
目的関数や凸関数、勾配法がわからない方は次の記事をみてください。
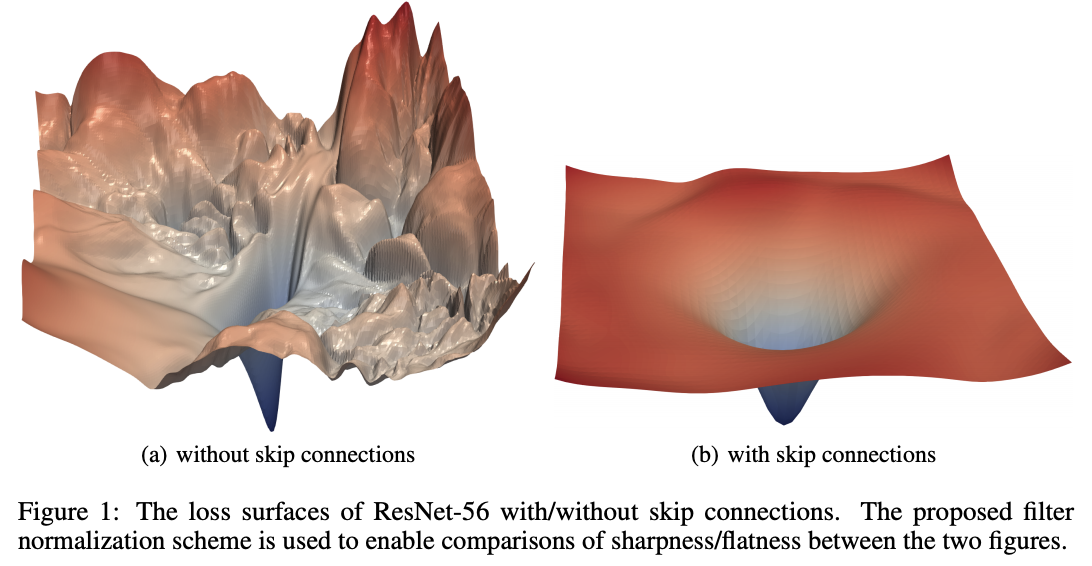
CNNの目的関数を可視化した論文があります。
その図をお借りして実際にどんな感じか見てみましょう。
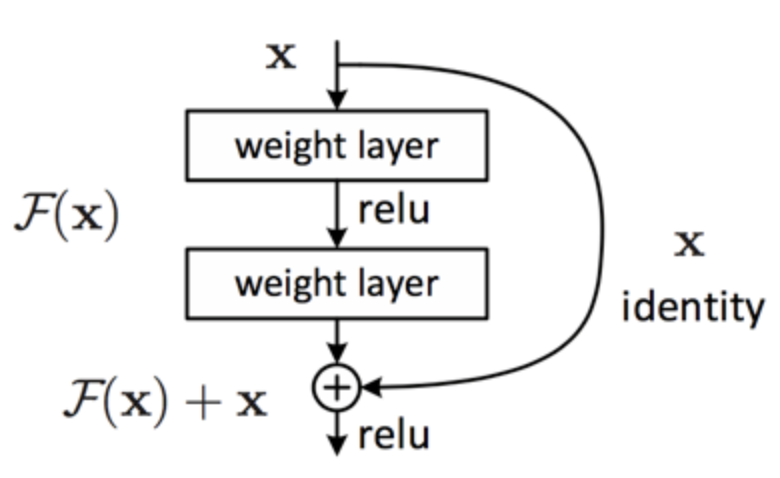
skip(residual) connectionとはResNetの特徴であるResidul blockの恒等写像のことです。
ちなみにこれは余談ですが、ResNetとXGBって考え方似てると思いませんか?
見ての通り左は明らかに凸ではないですね、右もマシではありそうですがサドルポイントが見られます。
別の図も見てみましょう。次のはCIFAR-10 datasetの学習の際のプロットになります。
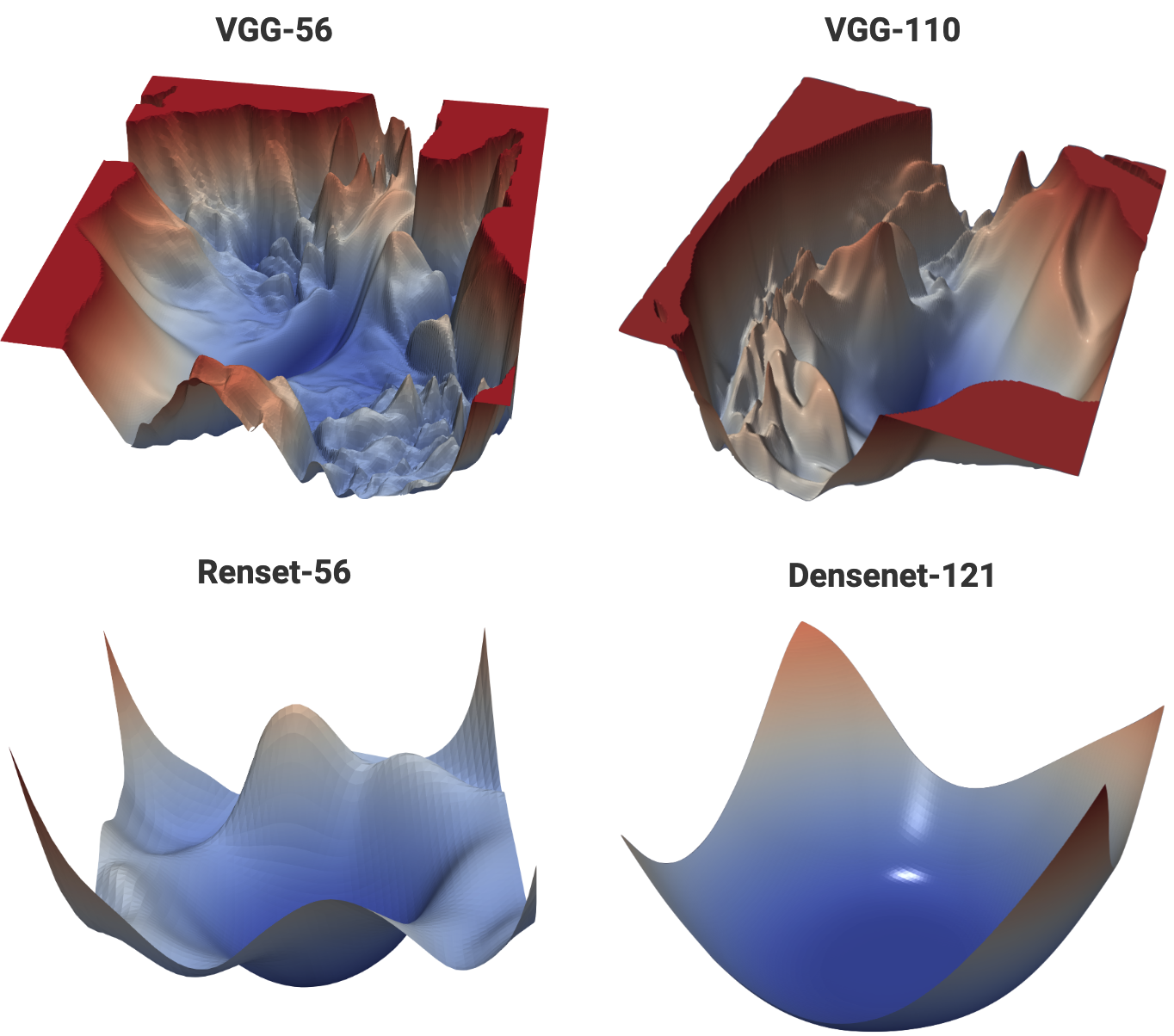
すごくないですか?何がってskip connectionのおかげで少し凸っぽくなってます。
VGGとDenseNetは初見なので調べてみました。というかいろんなモデル多過ぎ、、、
この際なのでニューラルネットワークのモデルをちょろっとみてみましょう。
そもそも現在流行りのCNNの基盤となったアルゴリズムはLeNet-5というものです。
開発者はフランス人のYann LeCun’s Home Pageです。
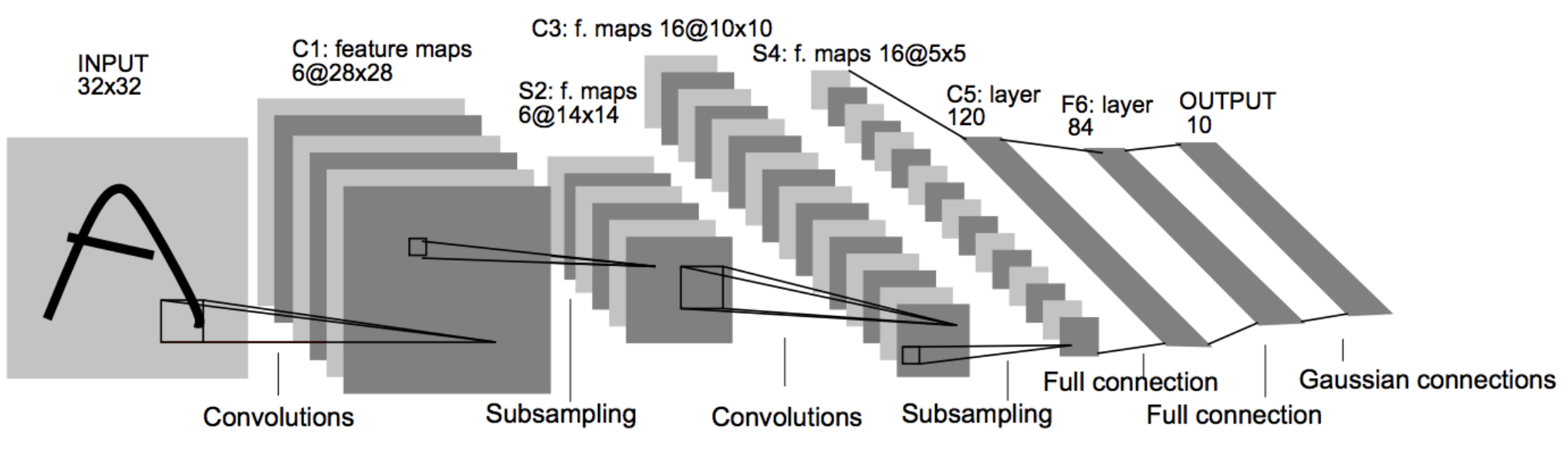
僕も最近知ったんですがこれ何がえぐいかって1998年に発表されているんです。
1998年ですよ?、どんな時代かググってみました。
パソコンの歴史/年代流行によると
1. Windows98発売
2. アップルが初代iMacを発売
だそうです。まだちょっとすごさがわからないので調べてみると
– Windows 98 – Virtual x86
– What’s iMac – AirMac
だそうです。言いたいことは今のスマホの足元に到底及ばないスペックです。
まあこの話は置いておいて、VGGとDensenetは僕は初見だったので調べてみました。
まずはVGGです。下のアーキテクチャは論文のものです。
2014年のアルゴリズムで当時はかなり深いとされていたようです。
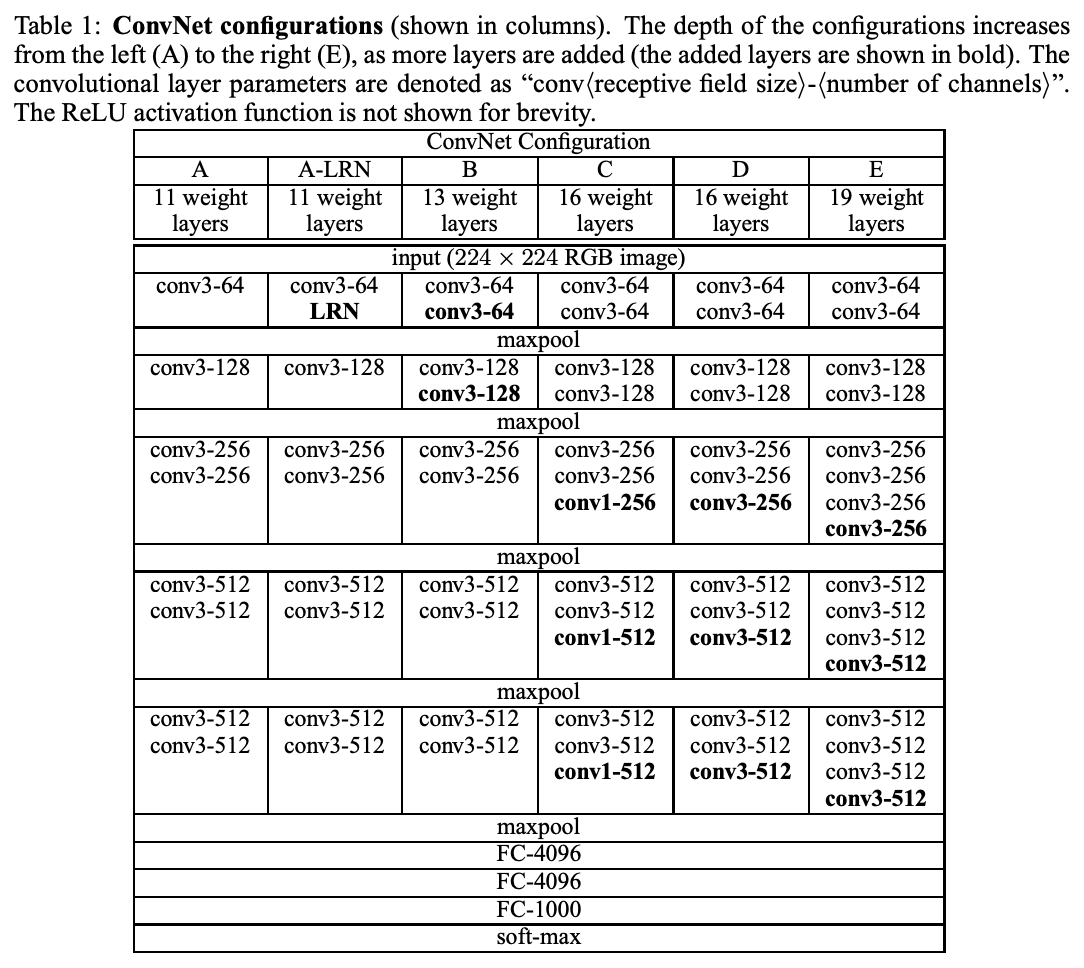
それほど喋ることが見当たらないのですが強いていうなら
このモデルのアウトプットベクトルが1000なので1000種類の画像を識別できます。
Fine Tuningすればあなたの好みの画像を分類できます。例えば、好みの女優とか?
なんでモデルを最初から作らずFine Tuningするのか?
という問に対する答えは、学習量が減るからのようです。
具体的には元々のモデル上層部の重みは学習データを変えてもそれほど変化しないようなので
そのまま使い下層部つまり出力層に近い重みを更新するようです。
入力が人からキリンとかになったらどうかと思いますがね、、、
続きまして、DenseNetです。
これはResNetの改良版と言えるでしょう。改良版というのは次のようにResNetを問題視したからです。
An advantage of ResNets is that the gradient can flow directly through the identity function from later layers to the earlier layers. However, the identity function and the output of H` are combined by summation, which may impede the information flow in the network.
そもそもResNetの背景には深層における勾配消失問題があります。
この対策としてidentity functionが導入されResNetができたのですがDenseNetでは
それはメリットである一方、モデルにおける情報フローを阻害していると考えたようです。
言われてみるとそうかも知れませんね。そこで考えたれた
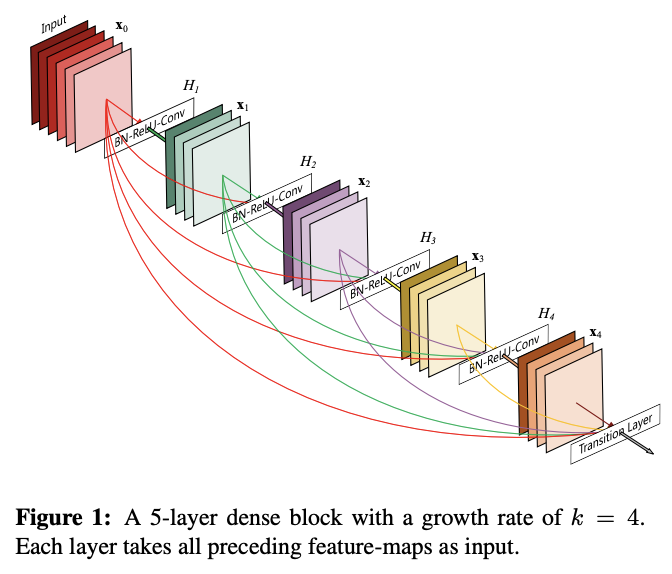
ResNetの特徴Residul blockに対するDense blockです。見ての通り前工程の出力を全て入力に使っています。
で、使われたモデルはこんな感じで
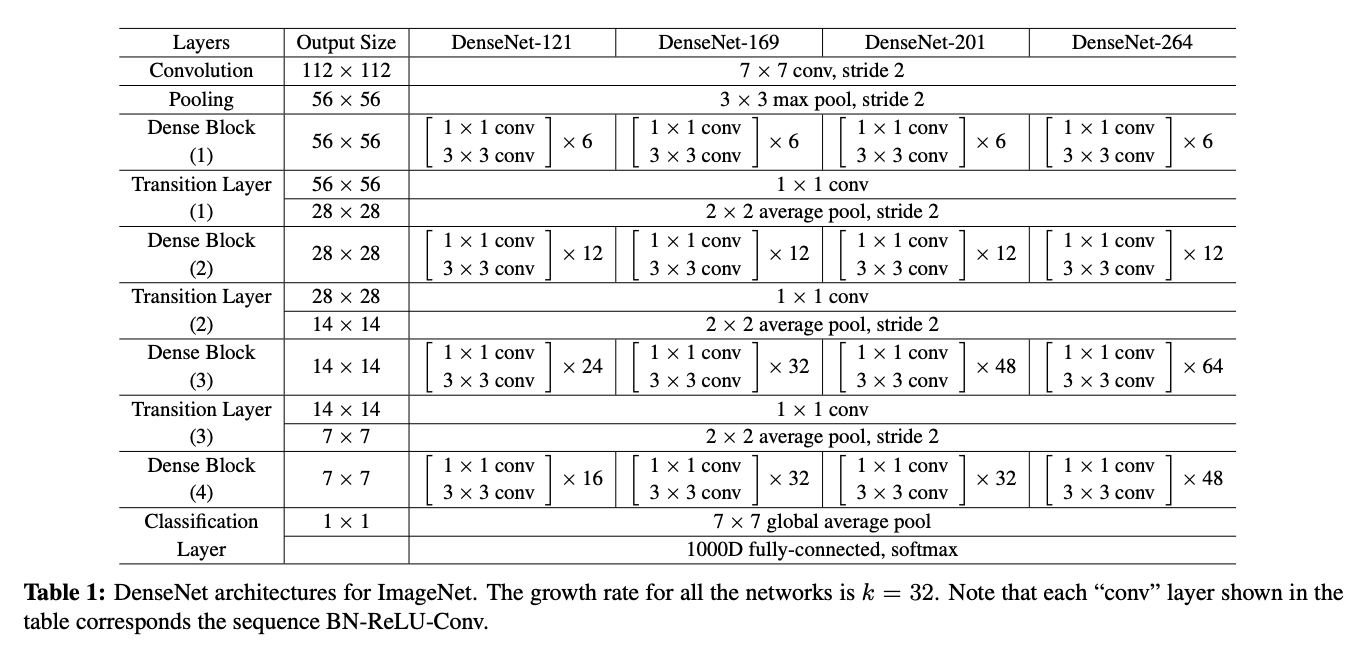
ResNet含め、その他のアルゴリズムとの比較結果がこれ
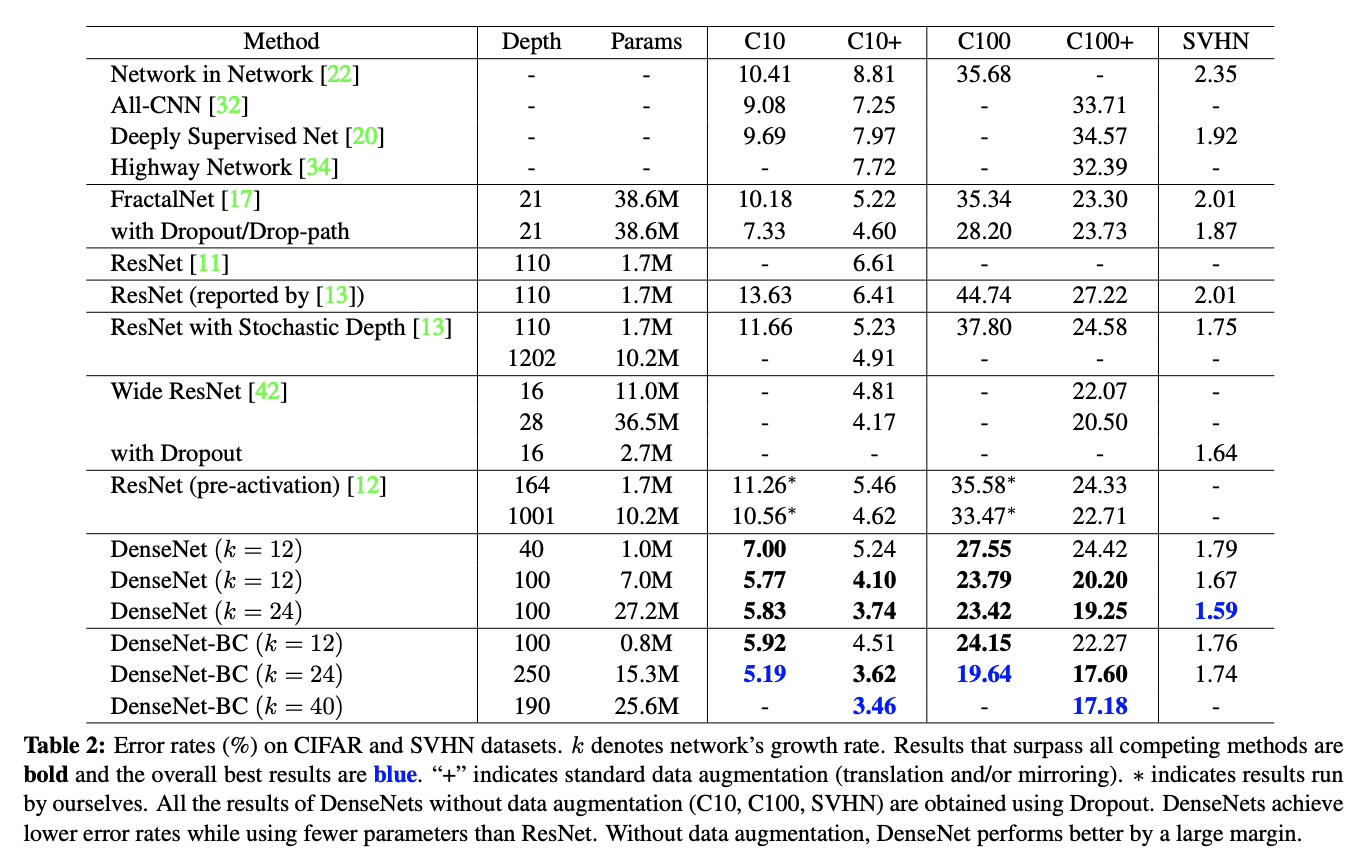
青の数値がDenseNetです。エラーが小さいのでいい精度であることがわかります。
長くなりましたがいろんなCNNと目的関数の凸性を見てみました。
ちなみにこれら全てkerasにあります。
– Applications
便利な時代ですね。。。。そしてこれらも勾配法使われていると思うとエグい、、、
でわ。