こんにちは。
Lassoでスパース、スパースと言ってましたが実際はスパース推定という言葉がよく使われます。これについての説明を軽くしてからGroup lassoの紹介をします。
スパース推定とは
スパースは”疎”を意味します。スパース推定とはどのパラメータが0になるかを推定すること。つまり、データの本質がわかります。直感的には次の図から
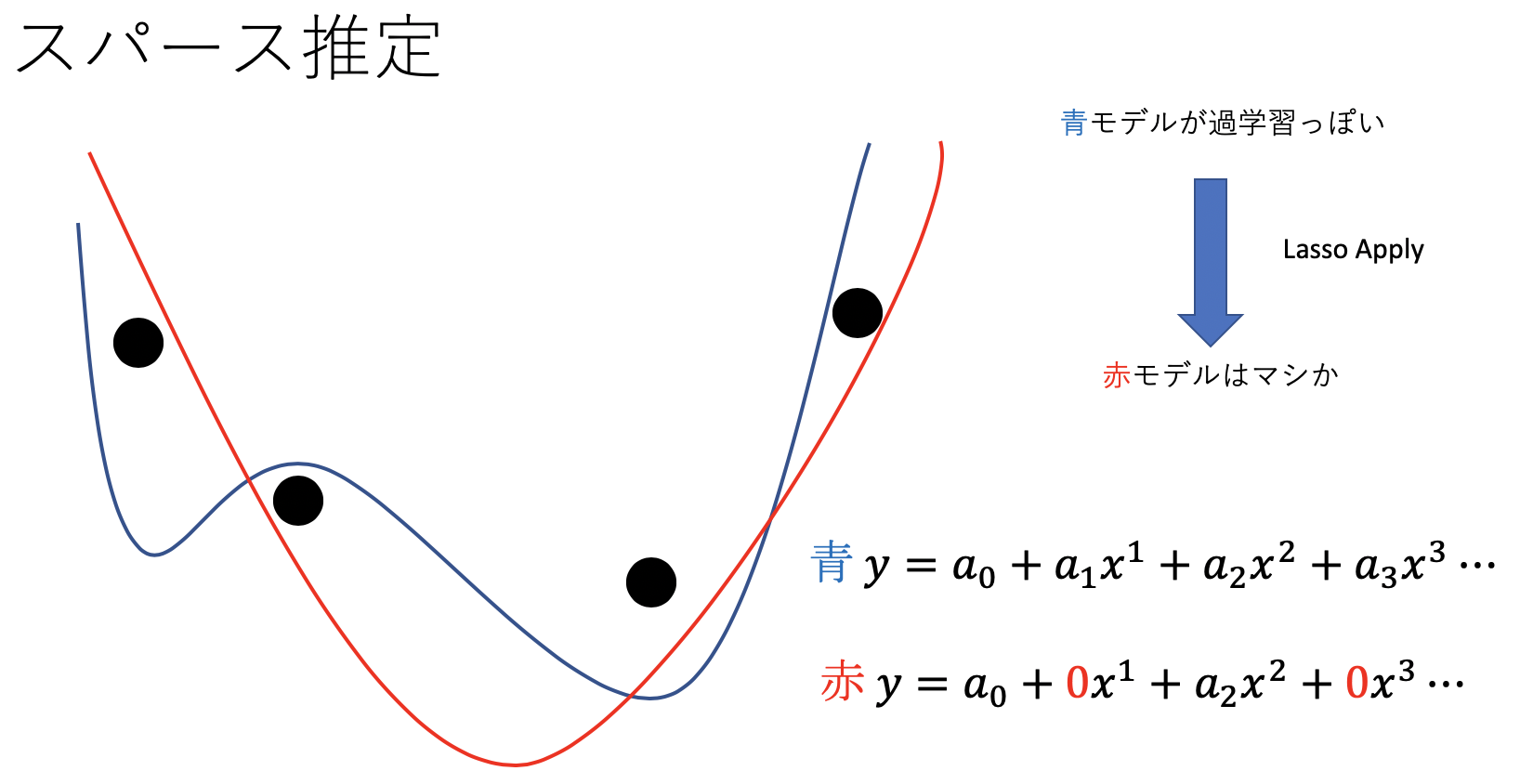
もう少し実用的な例は?
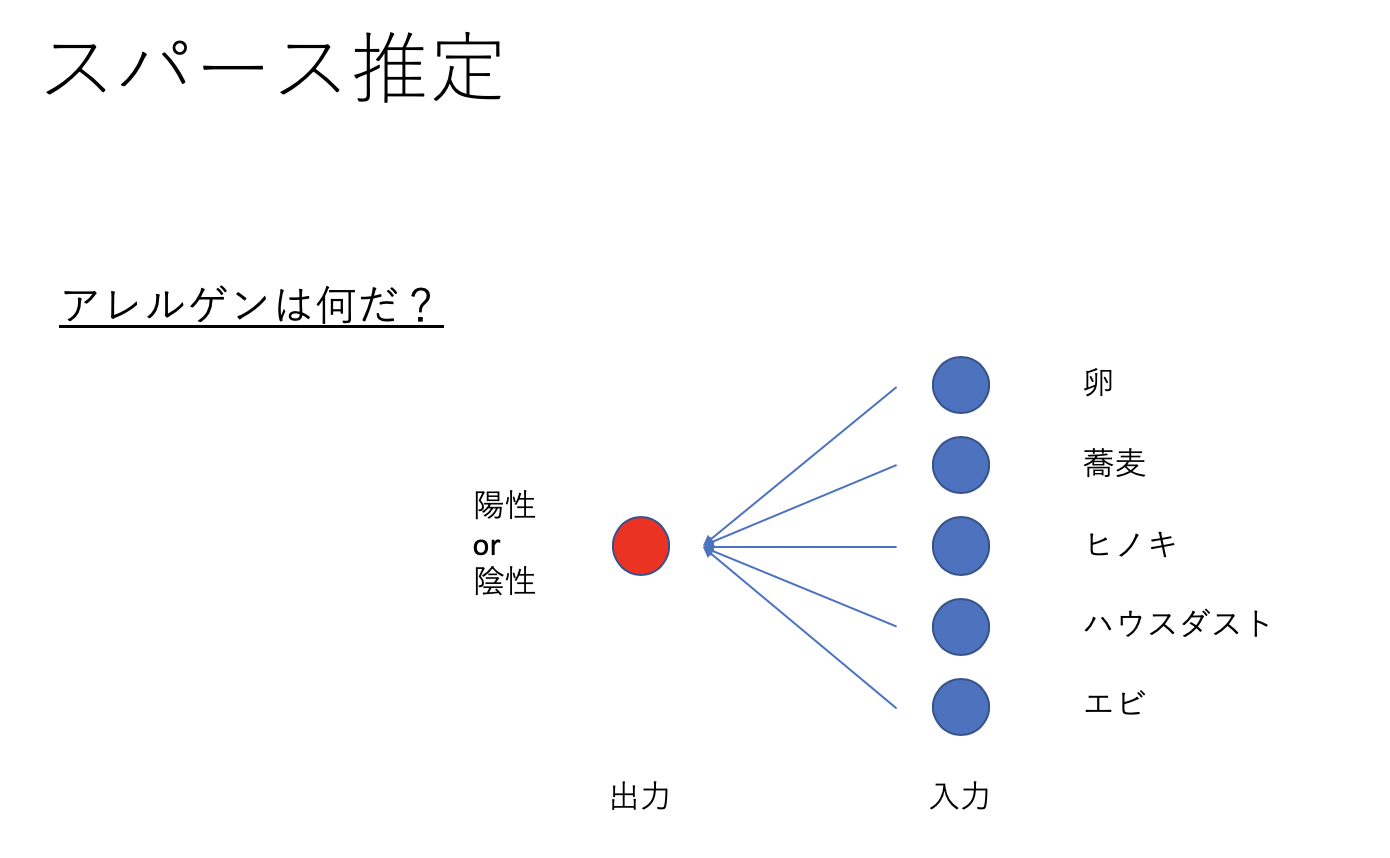
右の入力から左の出力を考えるLassoモデルを考えると
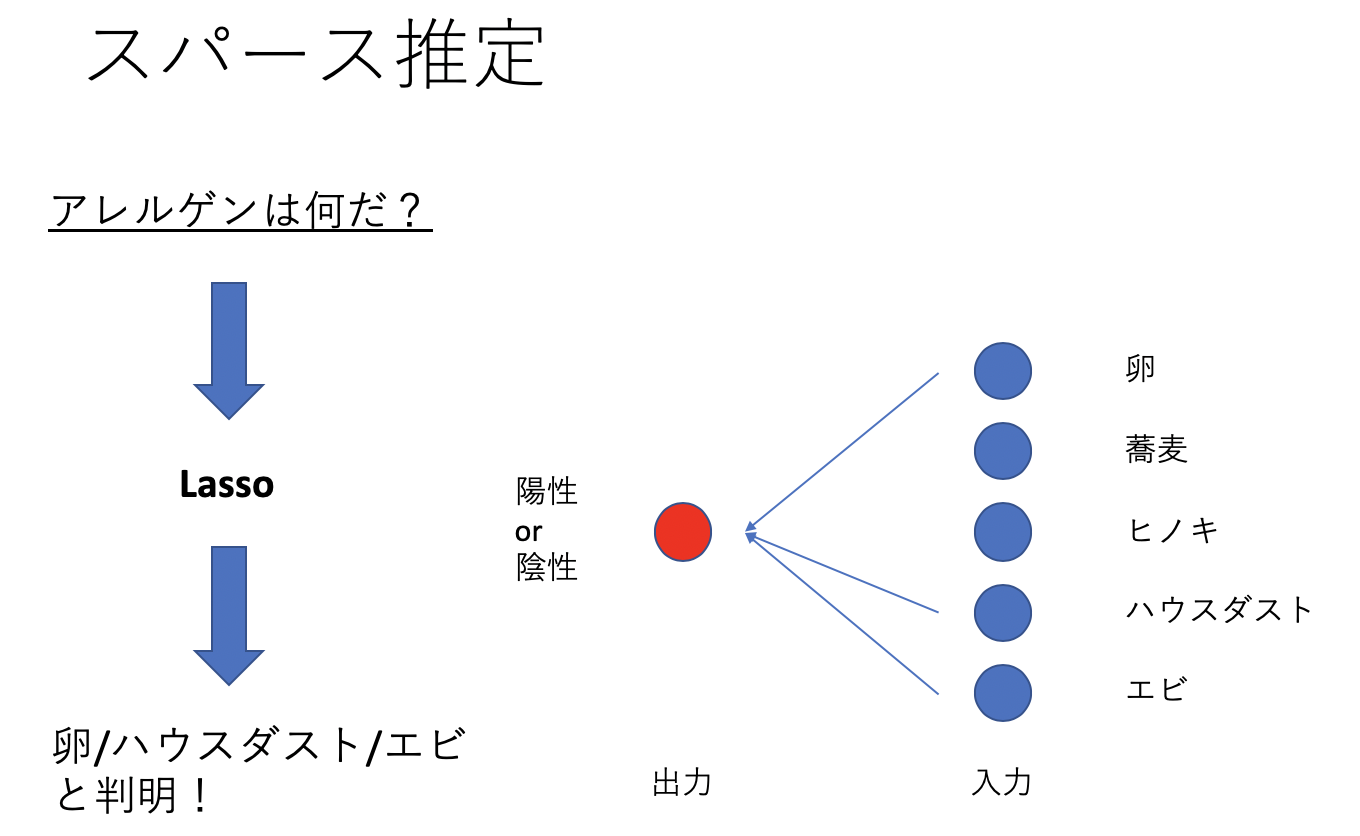
のようにアレルゲン反応のスパース推定ができます。
つまり、スパース推定により関与しないパラメータがわかります。
Group Lassoとは
グループラッソとは
先ほどのアレルゲンを例にとると例えば、ヒノキなどの個体単位ではなく「花粉」というグループ単位でスパース性が検証できるモデルのことです。Lassoはの正規化項は次のものでした。
![Rendered by QuickLaTeX.com \[\Omega_{Lasso}(\beta) = \sum_{i=1}^{n} |\beta_i|\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-3bda9999a35499c95d281fdd0f00c5ea_l3.png)
Group Lassoの正規化項は次で定義されます
![Rendered by QuickLaTeX.com \[\Omega_{Group}(\beta) = \sum_{g=1}^{G} \sqrt[]{p_g} |\beta_{g}|_2\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-48a2a72b579a16e703348b2c6b486fec_l3.png)
ここで![]() はg番目のグループを表すindex。(ただし、
はg番目のグループを表すindex。(ただし、![]() 、
、![]() はグループgの大きさ)
はグループgの大きさ)
前述通りGroup Lassoでは特徴をグループ化します。よって、事前に類似の傾向がありそうな特徴の情報を考慮します。
なるほど、と思った方と、ん?、と思った方がいると思います。
これは図を用いてチェックしましょう。
Group Lassoの解
- 参考文献の論文に従い、解説します。
まず![]() 個の変数からなるもっとも一般的な回帰問題を考えます
個の変数からなるもっとも一般的な回帰問題を考えます
![Rendered by QuickLaTeX.com \[Y = \sum_{j=1}^{J} X_j \beta_j + \epsilon\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-9a0f2a014cb0cd4ea12cf9e631ce0c56_l3.png)
Yは![]() ベクトル、
ベクトル、![]() 、
、![]() は
は![]() 番目のデータに対応した
番目のデータに対応した![]() 行列で
行列で![]() はサイズ
はサイズ![]() の係数からなるベクトルとする。さらに各
の係数からなるベクトルとする。さらに各![]() は直交行列であると仮定する。
は直交行列であると仮定する。
すなはち![]() とする。さらに、
とする。さらに、![]() 、
、![]() とすると上式は
とすると上式は![]() かける。
かける。
長ったらしく書きましたが要は「グループの大きさが各![]() のサイズ」です。なので
のサイズ」です。なので![]() を考えるとこれはLassoそのものとなります。
を考えるとこれはLassoそのものとなります。
![]() と
と![]() の正定値対称行列
の正定値対称行列![]() に対して次を定める。
に対して次を定める。
![]()
ただし、![]() とする。正定値行列
とする。正定値行列![]() が与えられた時、Group Lasso回帰では次の解を考える。ただし
が与えられた時、Group Lasso回帰では次の解を考える。ただし![]()
![Rendered by QuickLaTeX.com \[\frac{1}{2} | Y - \sum_{j=1}^{J} X_j \beta_j |^2 + \lambda \sum_{j=1}^{J} |\beta_j|_{K_j}\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-1f499999d9d45540e107fa4b726d20bb_l3.png)
Bakin(1999)はこれをグループ変数によるLassoの拡張版として提案しました。
ここも特に気にする必要はなく、大切なのは正定値対称行列![]() により変数に「重み」が掛かっているところです。機械学習ではこのように変数に重みを加える動作をよくします。一例として
により変数に「重み」が掛かっているところです。機械学習ではこのように変数に重みを加える動作をよくします。一例として
– マハラノビス距離(Mahalanobis distance)
があります。僕たちが無意識に距離として使っているものはユークリッドノルムで![]() 、つまり単位行列の時です。
、つまり単位行列の時です。
では先ほどの
をみましょう。
下の図はグループが2つ(各係数はベクトルとスカラー)、つまり![]() の場合を考え、
の場合を考え、![]() が単位行列の場合の正規化項を表しています(ラッソはダイヤ、リッジは円だったやつの三次元バージョン)
が単位行列の場合の正規化項を表しています(ラッソはダイヤ、リッジは円だったやつの三次元バージョン)
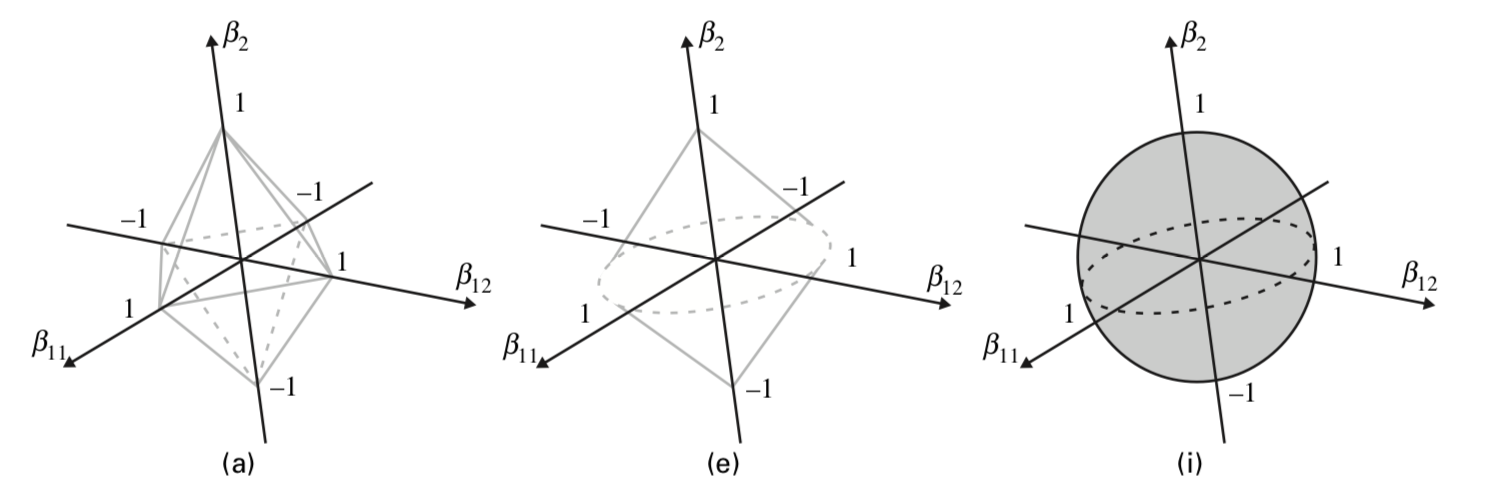
つまり、
- Figure(a)は
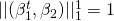
- Figure(e)は
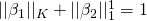
- Figure(i)は
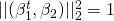
もっと噛み砕くと
- Figure(a)は Lassoの
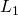 -norm
-norm - Figure(e)は GroupLassoのnorm
- Figure(i)は Ridgeの
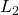 -norm
-norm
です。Figure(e)において![]() 平面を見ると
平面を見ると![]() というグループ単位でゼロに潰れることがわかります。
というグループ単位でゼロに潰れることがわかります。
だからGroup Lassoはグループ単位ででスパース性を与えているんです。
でわ。