こんにちは。 前回の最後に、 – Coordinate descent（座標降下法） – ISTA (メジャライザー最小化) – FISTA (高速化) の3つの最適化方法を紹介しました。今回は上の2つを解説します。そして次回実装へうつりましょう。 まずは簡単なLassoからです。

Coordinate descent

いきなり解説に入る前に何ですが、座標降下法ってメチャクチャシンプルなんですよ。 けど全く有名じゃないんですよね。（多分、理由は記事の最後）まあ、アルゴリズムみましょう
目的関数f(x) = g(x) + \sum_{i=1}^{n} h_i(x)の最適化を考えます。 ここでgはconvexかつdifferentiabl、h_i(x)はconvexとします。 （例えばconvexかつundifferentiablなf(x)を考えた場合、反例があります。詳しくはREADMORE） k=1, 2, \cdots回目の更新を右肩の添え字で表すと、各変数に対して

    \[x_1^{(k)} = \texttt{argmin } f(x_1, x_2^{(k-1)}, x_3^{(k-1)}, \cdots, x_n^{(k-1)})\]

    \[x_2^{(k)} = \texttt{argmin } f(x_1^{(k-1)}, x_2, x_3^{(k-1)}, \cdots, x_n^{(k-1)})\]

    \[x_3^{(k)} = \texttt{argmin } f(x_1^{(k-1)}, x_2^{(k-1)}, x_3, \cdots, x_n^{(k-1)})\]

のように更新するアルゴリズムです。
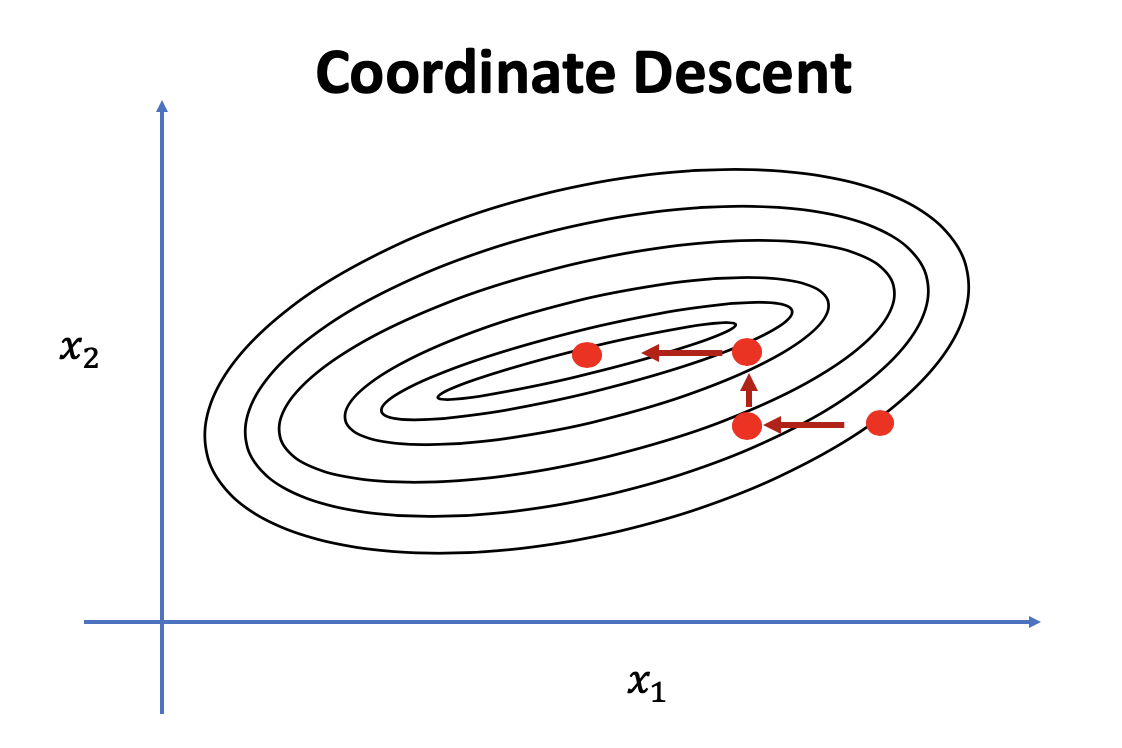
Pointは１つ、変数を１つずつ更新するんです。その他の変数は定数とみるんです。なので この図の感じですね。しかし次の問題を考えてみましょうx \in \mathbb{R}^2に対して

    \[\texttt{Minimize } x_1^2 + x_2^2 + 5|x_1 + x_2|\]

です。例えば初期値をx=(1,-1)で座標降下法をアプライしてみると x_1,　x_2のどちらから更新してもx=(1,-1)で停滞することがわかります。しかし これは明らかに最適解はx=(0,0)ですよね。こういったことからスパースな問題にはあまり良くないようです。 次にメジャライザーの方を行きましょう。

Iterative Shrinkage Thresholding

ちなみにこのアルゴリズムは初めて聞きました。EMアルゴリズムでも似たことが行われますね。 こちらもアルゴリズムは単純で
テイラー展開を行い、目的関数を置き換えることで最適化問題を解きやすい形にしよう
というものです。
一次元の場合、fをx=a周りでのテイラー展開

    \[f(x) \approx f(a) + f^{(1)}(a)(x-a) + \frac{1}{2!} f^{(2)}(a)(x-a)^2 + \frac{1}{3!} f^{(3)}(a)(x-a)^3 + \cdots\]

多次元の場合、

    \[f(\vc{x})= f(x_1,x_2, \ldots, x_n)\]

    \[f(\bf{x}) \approx f(\bf{a}) + Df(\bf{a}) (\bf{x}-\bf{a}) + \frac{1}{2} (\bf{x}-\bf{a})^T Hf(\bf{a}) (\bf{x}-\bf{a})\]

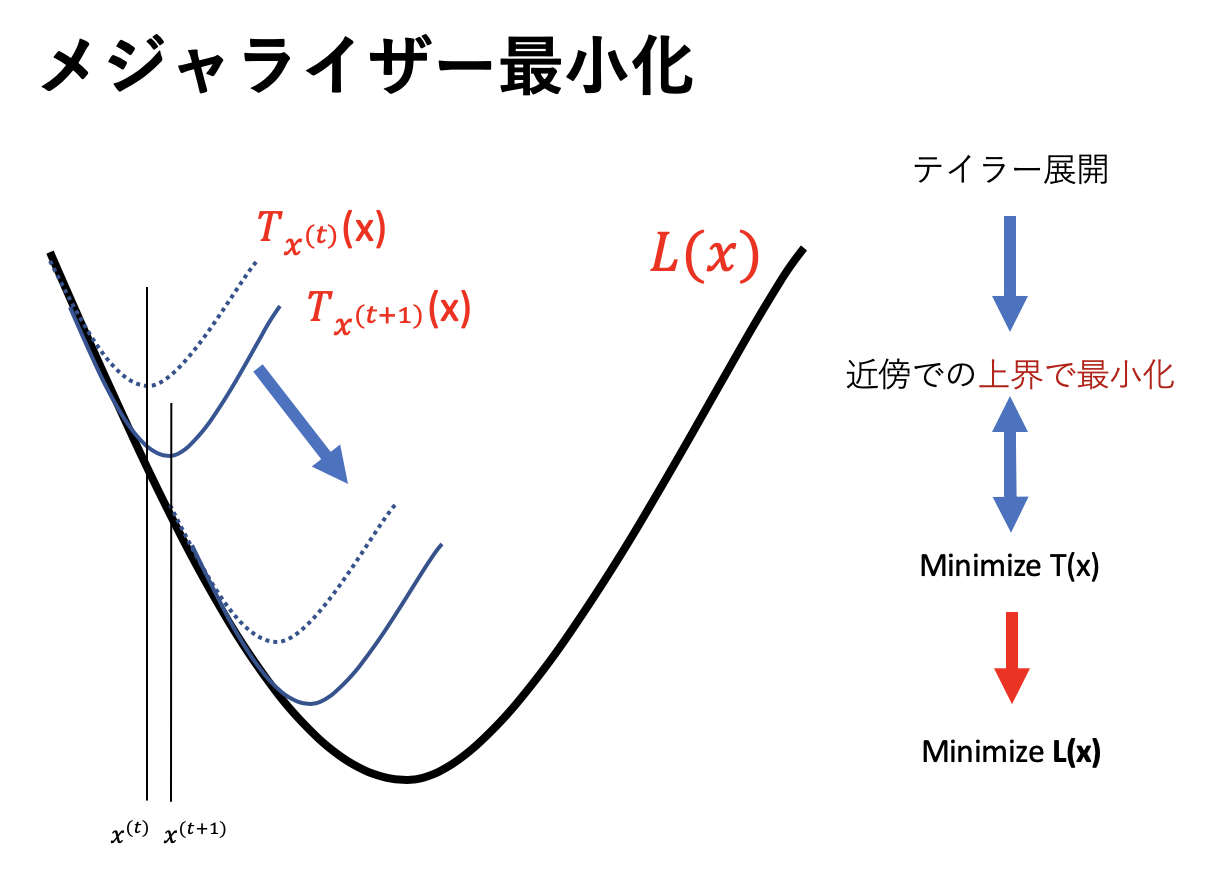
下の図がイメージになります。上界というのは「より大きいやつ」という意味です。 この図からアルゴリズムがどうやって動いて何で最適化できるのかは直感的にわかったかと思います。 しかし、このメジャライザーが本当に存在するのか？など疑問に思う人がいるでしょう。 では考察しましょう。 まず初期値をx^{(t)}とします。そして目的関数を\mathcal{L}(x),メジャライザーを\mathcal{T}(x)とします。 そして、メジャライザーは次のような性質を満たしてほしいです。 – \mathcal{L}(x^{(t)}) = \mathcal{T}(x^{(t)}) – \forall x\neq x^{(t)} に対して \mathcal{L}(x) \leq \mathcal{T}(x) すると性質から明らかにTの最小化がLの最小化に繋がることがわかります。 では実際にそんな都合のいい\mathcal{T}(x)を探しましょう。の前にちょっと寄り道します。

どんな形のメジャライザーが都合いい？

メジャライザーT(x)を探すといえどこのままでは全くわかりません。 T(x) = x^2にすればいいのか？いや、それもわかりません。なので
都合のいいメジャライザーの形を予想します。
いきなりですが次の最適解xを考えましょう。次元は１です。(\lambda \geq 0)

    \[\texttt{argmin } \frac{1}{2} (y-x)^2 + \lambda |x|\]

前回の記事でやったようにこれは場合分けで簡単にできますね \forall x \geq 0に対して

    \[\frac{1}{2} (x^2 - 2xy + y^2 + 2\lambda x) = \frac{1}{2} (x - (y-\lambda))^2 + \texttt{const}\]

同様にして\forall x < 0に対して

    \[\frac{1}{2} (x - (y+\lambda))^2 + \texttt{const}\]

では最後にyの範囲で場合分けすると前回のSoft thresholding functionが出てきましたね。

    \[x = S ( y, \lambda )\]

詳しく復習すると y < - \lambdaの時

    \[x= y + \lambda\]

- \lambda \leq y \leq \lambdaの時

    \[x = 0\]

y > \lambdaの時

    \[x = y - \lambda\]

これが大切です。
　つまり平方完成して解が求まりました。
ではLassoの目的を再掲しましょう。

    \[\texttt{argmin } ||y - Xb||_2^2 + \lambda|b|_1^1\]

今の例と似てますよね。
　しかしここままでは平方完成できない
ここで
　平方完成できるやつを考えよう！！！
これがほしいメジャライザーを予測するということです。 では元に戻って都合のいい\mathcal{T}(x)を探しましょう。平方完成できるやるがいいんでしたね。 テイラーの２次近似の形を想像しながら

    \[\mathcal{T}(\mathbf{x}) = \mathcal{L}(\mathbf{x}^{(t)}) + \frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}(\mathbf{x} - \mathbf{x}^{(t)}) + \frac{\rho}{2}\bigl\vert\mathbf{x}-\mathbf{x}^{(t)}\bigr\vert^2\]

という形で考えましょう、(\frac{\rho}{2}は計算の都合上のもの)そうすれば

    \[= \frac{\rho}{2} \Bigl\vert \bigl( \mathbf{x}^{(t)} - \frac{1}{\rho} \frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}\bigr) - \mathbf{x} \Bigr\vert^2 + \texttt{const}\]

とできますね。よって

    \[\text{argmin } \Bigl(\mathcal{T}(\mathbf{x}) + \lambda |\mathbf{x}|\Bigr)\]

は

    \[x^{(t+1)} = S \Bigl( \frac{1}{\rho} \frac{d\mathcal{L}(\mathbf{x}^{(t)})}{d\mathbf{x}}, \lambda \Bigr)\]

となります。
　実はまだ終わっていない
そうなんです。先ほどメジャライザーを考えたときに\rhoを使いましたね。 この\rhoを決める必要があります。メジャライザーの性質（２）から

    \[\mathcal{T}(\mathbf{x}) - \mathcal{L}(\bf{x}) = \frac{1}{2} (\bf{x} - \bf{x}^{(t)})^\top (\rho I - X^TX) (\bf{x} - \bf{x}^{(t)})\]

が「０以上」を任意の\bf{x}について言える必要があるので
　(\rho I - X^TX)が半正定値
の必要があります。つまり、X^TXの最大の固有値が\rhoとして取りうる最小の値になります。 そこで固有値の大きさを見積れる定理があるのでそれを使いましょう。 – Gershgorin circle theorem – Gershgorin’s Theorem for Estimating Eigenvalues この定理からmaxをとることで

    \[\texttt{eigenvalue } \le \max_j \sum_i\bigl\vert{\mathrm{X^\top X}}_{ij}\bigr\vert\]

と固有値の大きさが見積もれます。 長かったですがとりあえずLassoはおしまいです。
でわ。

READMORE