ホーム » その他 » ねぇPython、Parametric testって何？（理論編）

ねぇPython、Parametric testって何？（理論編）

投稿者: in その他 投稿日:

こんにちは。

前回はNormality testをやりました。ガウス分布に従うかどうかをチェックするものでしたね。今回はその他のParametric testをやりましょう。簡単に復習するとデータに特定の分布を仮定する検定でした。

さて、前回the test statisticというワードを説明した際にz-statistic、t-statisticという例を書きました。これはなんでしょう？

統計量

と呼ばれるもの。以下、例

  1. z-statistic

        \[ z = \frac{\bar{x} - \mu }{\sqrt{ \frac{\sigma^2}{n} }} \]

  2. t-statistic

        \[ t = \frac{\bar{x} - \mu }{\sqrt{ \frac{s^2}{n} }} \]

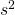    ここで、s^2は不偏分散(nが多くない時に使うやつ)

これは使う検定によってことなります。したがって検定を決めると同時に決定されます。また、これはp-valueの計算に使われるといいました。

p-値？

これは帰無仮説H_0のもとで統計量の実現値、つまり実際にデータから計算された統計量が得られる確率。計算は下の方で紹介する標準正規分布表を使うのですがめんどくさいのでこことかをつかいます。

これは有意水準(足切りのようなもの)と比べられます。なので例えば、

「俺の友達の身長の平均は190cmだ」という帰無仮説H_0を立てる。実際に友達の身長を聞いて集めまくる。z-testをするとする。よってz-statisticを用いる。z=2だったとします。p-valueを計算すると0.0455だった。有意水準を5%とすると。0.0455 < 0.05よりH_0は棄却され、190cmではないと言える。一方、有意水準を1%とすると。0.01 < 0.0455よりH_0は採択され、平均が190cmではないとは言えない。

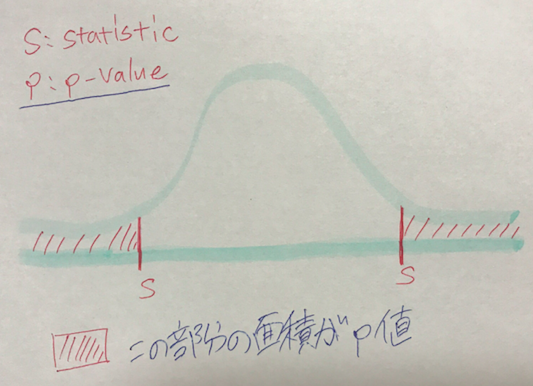
有意水準と比べるという意味を可視化してみると次の通り。

つまり、珍しすぎてもうあり得ないという理由でH_0を棄却するときの珍しさ具合が有意水準です。ちなみに、こうやって両側使う検定を両側検定、片側のみを片側検定をいいます。H_0: \mu = 0としたとき前者、後者の対立仮説はそれぞれH_1: \mu \neq 0, H_1: \mu > 0のようになります。(ここが詳しい)

さて、軽く復習ができたので本題に入りましょう。

母集団の平均に対する検定

がテーマです。先に言っちゃうとstudent-T-testをやろうと思います。しかし、まずは馴染みのあるガウス分布を使ったz-testから触れていきましょう。

中心極限定理を覚えていますか？

どんな母集団でも平均\mu・分散\sigma^2のとき、十分多く(n\geq 30)の標本を取れば

    \[\bar{X} \sim \mathcal{N}(\mu, \frac{\sigma^2}{n})\]

つまり、「データが超多かったら正規分布使えるで」ってことです。

中心極限定理と標準化を使ってz-test(z-検定)をするときは統計量(statistic)はz-statistic(z-valueともいう)で

    \[ z = \frac{ \bar{x} - \mu }{ \sqrt{ \frac{\sigma^2}{n} } } \sim \mathcal{N}(0, 1)\]

を使います。前述通り母集団の平均に対する検定なので例えばH_0: \mu = 5、H_1: \mu \neq 5などとして検定します。有意水準を5%とすると標準ガウス分布表を用いて

    \[P(|z| \geq 1.96) = 0.05\]

とわかります。例えばz=-2.5となれば上を満たすのでH_0は棄却されます。この時の1.96という値をcritical valueといいます。

ちょっと待つんだ

母集団の分散とかわからんやん!

そうです。母集団の分散がわかってなかったらこのz-testはできないんです。というか実世界で母集団の分散が分かっている状況なんてあるんだろうか、、、

諦めない！まだ方法はある

スチューデント t 検定

母集団の分散がわからんから代わりに不偏分散(nが多くない時に使うやつ)を使いましょう。これをつかって同様に標準化する！すると

自由度n-1のt分布に従う
(nはサンプルサイズ)

よって

    \[ t = \frac{ \bar{x} - \mu }{ \sqrt{\frac{s^2}{n} } } \sim t(n-1)\]

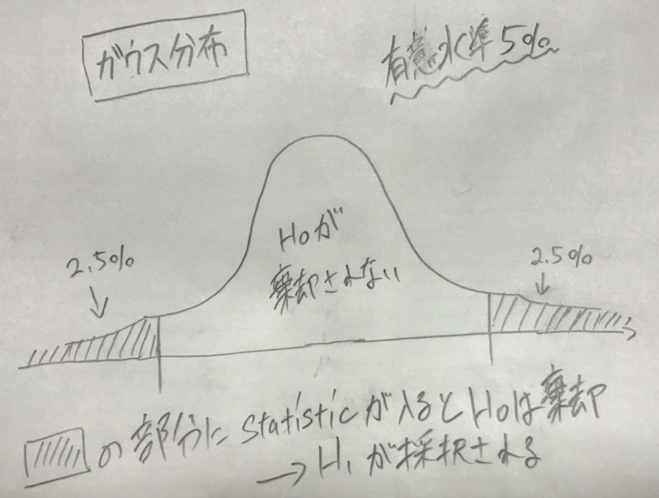
となります。分母をnoise、分子をsignalといいます。ここまでくればt分布表を用いてさきほどと同じことをするだけですね。(例題)

今までは１つのデータセットを扱って検定していました。しかし、2つのデータセット(n個,m個)を使って検定したときありますよね。

あいつと俺の間にモテ具合の差があるのか？

次の図をみてください。

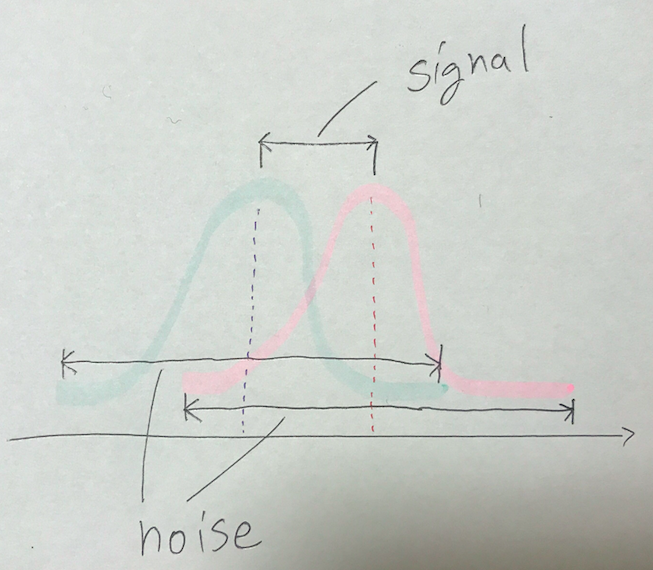
これは「似た分散」をもつ一次元ガウス分布に従う2つのデータです。これらの平均値の間に差があるかどうかを検定したいです。それぞれ\bar{x} \sim \mathcal{N} (\mu_1, \frac{\sigma_1^2}{n} ), \bar{y} \sim \mathcal{N} (\mu_2, \frac{\sigma_2^2}{m} )のときその差の分布も正規分布になるという再生性を使います。つまり

    \[\bar{x} - \bar{y} \sim \mathcal{N} (\mu_1 - \mu_2, \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} )\]

ここでもし\sigma_1^2 = \sigma_2^2なら(あくまで仮定)その推定量を

    \[ \sigma'^2 = \frac{ (n-1)\sigma_1^2 + (m-1)\sigma_2^2 }{n+m-2} \]

としH_0: |\mu_1-\mu_2| = 0であるもとで標準化すると自由度n+m-2で

    \[ t = \frac{ \bar{x} - \bar{y} }{ \sqrt{\frac{\sigma'^2}{n} + \frac{\sigma'^2}{m} } } \sim t(n+m-2) \]

とでき同じように検定できます。

え、\sigma_1^2 \neq \sigma_2^2なら？

そんなあなたに

ウェルチ検定

この時は

    \[ t = \frac{ \bar{x} - \bar{y} }{ \sqrt{\frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} } } \sim t(?????) \]

としますが、?????のところ、つまり自由度が複雑になります。

    \[????? = \frac{ \{ \frac{\sigma_1^2}{n} + \frac{\sigma_2^2}{m} \}^2 } { \frac{ \left( \frac{\sigma_1^2}{n} \right)^2 }{n-1} + \frac{ \left( \frac{\sigma_2^2}{m} \right)^2 }{m-1} } \]

とします。

なんでこの検定でわかるんだ

という問には答えられません。ガウスさんたちに聞くしかないです。他にもあるお店にお客が来る時間間隔は指数分布に従うなどといいますが理由はわかりません。事故回数で有名なポアソン分布も同じ。

今回の内容は統計検定、もしくはアクチュアリーちっくなものになりました。用語がたくさんあって混乱する範囲のようですがワンステップづつ確認しましょう。重要なのは中心極限定理です。他にも独立性のカイ二乗検定などあるので調べてみてください。

 

でわ。

READMORE

タグ: ,

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です