ねぇPython、Normality Testって何？（理論編）

2019.01.06

機械学習

こんにちは。

パラメトリックですね

っていいたくないですか？、とはいえそもそもパラメトリック・ノンパラメトリックとはなんぞや？

Parametric test データの母集団のパラメータ、つまり特性についてなんらかの仮説を立てた検定　(正規分布とか)
NonParametric test いかなる仮説も立てない検定

よし、ひとまずはこれで違いはわかりましたね。機械学習の本とか論文ではよく正規分布に仮定して話が進められます。(Autoencorderや変分ベイズやほかにもたくさん)なのでパラメトリックが主流なのでしょう。さて、ここではタイトルにあるように検定について話を進めていこうと思います。

どうやって使い分ける？

もちろんこう思いますよね。このタイミングでパラメトリックを仮定して良いのか否か。チェックする必要があります。今回はNormality Testでパラメトリックの妥当性、ガウス分布である妥当性を調べます。Normality Testは大きく分けて２パート。

Graphical Methods 名前の通り可視化してガウス分布っぽいか見る
Statistical Tests なんらかの検定によりガウス分布っぽいか調べる

では見ていきましょう、の前にあと少しだけ用語の解説です。

Hypothesis testing データの母集団のパラメータに関する仮説を検定すること — Null hypothesis 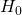$H_0$ で表される。棄却されることを目的とした仮説 — Alternative hypothesis 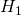$H_1$ で表される。 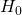$H_0$ が棄却された時に採択する仮説
p-value 仮説の妥当性を評価する数値。Null hypothesisが正しいと仮定した際にその結果が得られる確率。0.05より小さければ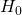 $H_0$ は棄却される。(0.01と比べる時もある)
The test statistic データから算出され、Hypothesis testingに使われるランダム変数。p-valueにも使われる。 (Z-statistic, t-statistic, F-statisticとか)
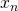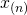order statistic 観測順序付きのサンプル。例えば、 $x_n$ と $x_{(n)}$ は別物、前者はn番目のサンプルであり、後者はn番目に観測されたサンプル

さて、いくつか検定について見ていきましょう。

Shapiro-Wilk Test https://en.wikipedia.org/wiki/Shapiro–Wilk_test

$W = \frac{ \left( \sum_{i=1}^{n} a_ix_{(i)} \right)^2 }{ \sum_{i=1}^{n} \left( x_i - \bar{x} \right)^2 }$

ただし

$(a_1, \cdots, a_n) = \frac{m^T V^{-1} }{ ( m^T V^{-1} V^{-1} m^T )^{1/2} }$

$m = ( m_1, \cdots, m_n)^T$

$m_i$ はiid(独立同分布)のorder statisticの期待値で $V$ はその共分散行列。Samuel Shapiro and Martin Wilkによって導かれた。分散の比で計算される。スケールに対して不変である証明が論文にあった。不特定の分布を評価するためにある。(平均、分散未確定)