こんにちは。 パラメトリック検定を終えて今回はノンパラメトリック検定についてです。僕も初見なので少しワクワクしています。早速いきましょう。 Mann Whitney U Test (Wilcoxon Rank Sum Test) これは独立な２つのグループのデータについて母集団分布の同一性を検定します。なので

H_0 : The two populations are equal

H_1 : The two populations are not equal

となります。パラメトリック検定では母平均に対して検定を行なっていましたがマン=ホイットニーのU検定では母集団分布を検定するんですね。また、これは両側検定が一般的です。もし片側検定をするのであれば対立仮説は母集団分布に対してのシフトになります。で、特徴量についてですが、

    \[ U_1 = n_1n_2 + \frac{n_1(n_1+1)}{2} - R_1 \]

    \[ U_2 = n_1n_2 + \frac{n_2(n_2+1)}{2} - R_2 \]

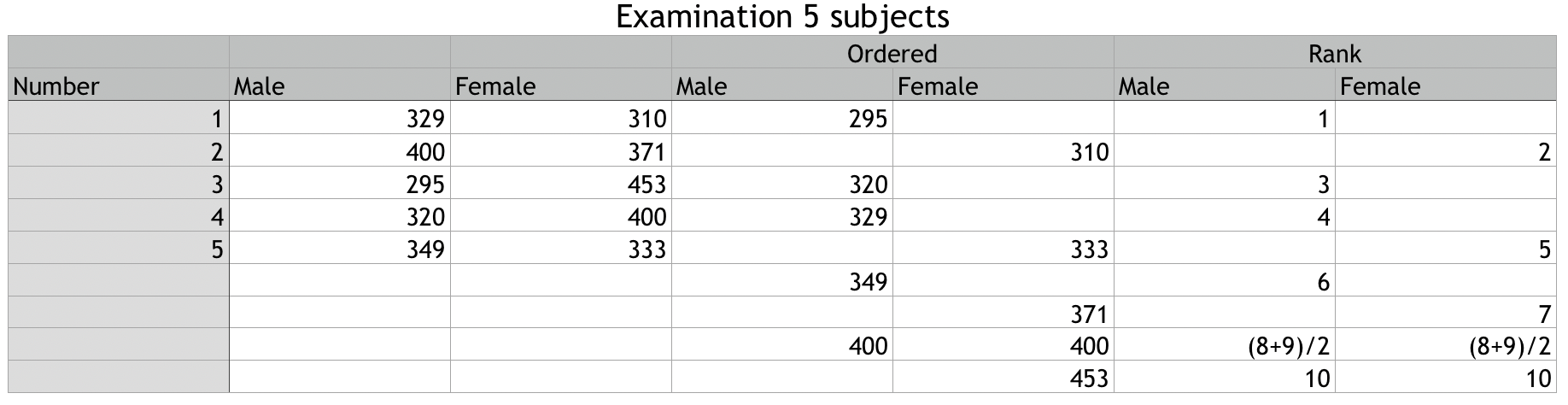
となります。データを小さい順に並べてrankづけして行った時の各グループのrankの総和がR_1,R_2なんですが、下の図で説明します。 この場合だとR_1 = 32.5, R_2 = 32.5です。

独立じゃないときは？(i.e. matched or paired)

たとえば　The sign test これは最もシンプルなノンパラテストで中央値の差を検定します。ちなみに、独立じゃない時、と言いましたがこれはたとえば同じグループで実験した際に得られるデータとかになります。なので

H_0 : The median difference is zero

H_1 : The median difference is not zero α=?

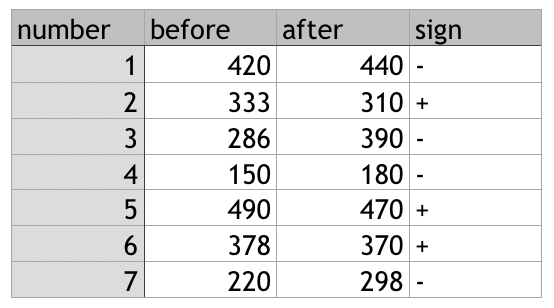
となります。これは各データの増減を比較し減っていれば＋、増えていればーという風に符号づけします。以下、例として７人の生徒の５教科の総得点を試験対策前と試験対策後を考えます。 で、どうやるかというとp値を計算します。

どうやって？

\pmを裏表とみていつもの二項分布(p=0.5)を考えます。N個のデータがあって符合づけした時、r個マイナスがあったとします。するとp値は

    \[ p = P(X \leq r)= \sum_{i=0}^{r} \binom Ni p^i (1-p)^{N-i} \]

これを有意水準\alphaと比べます。見ての通りこれは片側検定です。両側検定の場合はこのp値を2倍すればいいことが

P(X\leq r) = P(X\geq N-r)

からわかります。

\pmだけで判断するのはええのか？

なんか雑な感じしますよね。そこで次の方法があります。 Wilcoxon Signed Rank Test 符号検定の改良版で、左の具合、大きさに注目します。先ほどのデータを用いて 帰無仮説と対立仮説は符号検定の時のものと同様です。で、統計量Wは次W_+,W_-の小さい方で定義されます。そしてそれぞれを各符号を持ったrankの絶対値総和となります。なので

W_+= 1+2.5+4=7.5

W_- = |-2.5|+|-5|+|-6|+|-7| = 20.5

です。W_+,W_-の作り方からもし帰無仮説が正しければこれらはともに小さい値になるはずです。で、critical valueは例えばこの表からわかります。この例だとcritical valueは4となり、W=W_- \geq 4よりH_0は棄却されません。 今までは２種類のデータを対象にしていました。2つ以上を対象としたい時はKruskal Wallis Testを使います。これについてはまた次回書きます。   でわ READMORE