こんにちは。前回、射影行列を学びました。![]() 次元ベクトル
次元ベクトル![]() を考えよう。行列
を考えよう。行列![]() の列ベクトルが作る空間の中でもっとも
の列ベクトルが作る空間の中でもっとも![]() に近いものは
に近いものは![]() という形で表された。ただし、
という形で表された。ただし、![]() は縦ベクトルとすると
は縦ベクトルとすると
(1) ![]()
となりこれがもっとも![]() に近いヤツで
に近いヤツで
![]()
Vの列ベクトルがはる空間への射影行列
だった。今回はその![]() はどんなやつ?か考える。つまりどんなベクトルが作る空間へ射影すればいいんだ?ということ
はどんなやつ?か考える。つまりどんなベクトルが作る空間へ射影すればいいんだ?ということ
データ![]() (m次元)
(m次元)
平面を貼るベクトルを![]()
ただし![]() ,
, ![]()
とする。目標は![]() を見つけ出すこと。計算の前にいくつか確認しておこう。
を見つけ出すこと。計算の前にいくつか確認しておこう。
- 実対称行列の固有ベクトルは直行
- 実対称行列は対角化可能
- グラムシュミットで正規直交基底が作れる
- tr(AB) = tr(BA)
- x^T A x = tr(x^T A x)
まず、3番より射影行列![]() は次のようになる
は次のようになる
![]()
ではどうやって![]() を決定するかだが、前回同様、分散を最大化させる作戦でいこう。射影後の分散が最大化されるように
を決定するかだが、前回同様、分散を最大化させる作戦でいこう。射影後の分散が最大化されるように![]() を決定したいので
を決定したいので
(2) 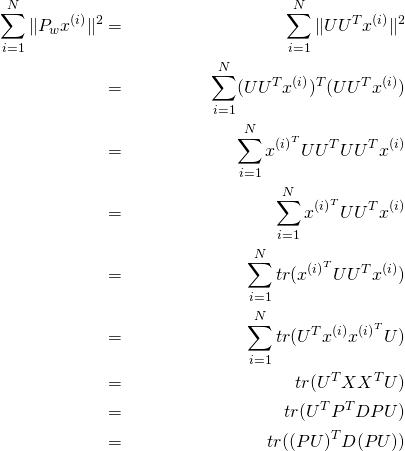
ここで、対称行列![]() を
を![]() と変形しました。これを行列の対角化といいます。ここで、Pは固有ベクトルを基底とした空間から標準基底の空間への変換行列なんですが、重要なことは基底(軸)の取り方によって座標が変わるということでしたね。これを踏まえて
と変形しました。これを行列の対角化といいます。ここで、Pは固有ベクトルを基底とした空間から標準基底の空間への変換行列なんですが、重要なことは基底(軸)の取り方によって座標が変わるということでしたね。これを踏まえて
![]()
を最大化させる![]() の形を考えよう!例えば
の形を考えよう!例えば
![Rendered by QuickLaTeX.com \[ tr \left( \begin{pmatrix} a & b & c \\ d & e & f \\ \end{pmatrix} \begin{pmatrix} 12 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} a & d \\ b & e \\ c & f \end{pmatrix} \right)\]](https://research.miidas.jp/wp-content/ql-cache/quicklatex.com-d0b7f484d8b9901d3f3fb551ea48d044_l3.png)
において![]() を正規直交とするときどんなものがトレースを最大化させるか?
を正規直交とするときどんなものがトレースを最大化させるか?
![]()
しかないのは明らか。よって![]() の列ベクトルには固有ベクトルが並べばいいことがわかります。実際、例えば
の列ベクトルには固有ベクトルが並べばいいことがわかります。実際、例えば![]() が最大固有値
が最大固有値 ![]() に対応する固有ベクトルとする時
に対応する固有ベクトルとする時![]() は
は![]() となる(Pが座標変換するから)
となる(Pが座標変換するから)
(3) ![]()
となるからです。従って射影行列![]() の
の![]() は列ベクトルとして固有ベクトルを並べればいいことがわかりました。
は列ベクトルとして固有ベクトルを並べればいいことがわかりました。
次回はこれを実装で確かめましょう。
でわ