ねぇPython、線形回帰って何？（理論編）

2018.11.08

機械学習

こんにちは。勾配法を終えました。差分法も終えました。目的関数も終えました。いい流れですねえ。余談ですが最近、友人に機械学習の入門書を選んでくれと言われ書店へ行ったのですがブームってすごいですね。今やいい本がたくさんあります。コードも丁寧に説明してあって数式も導出してあって、、、今回のデータセット

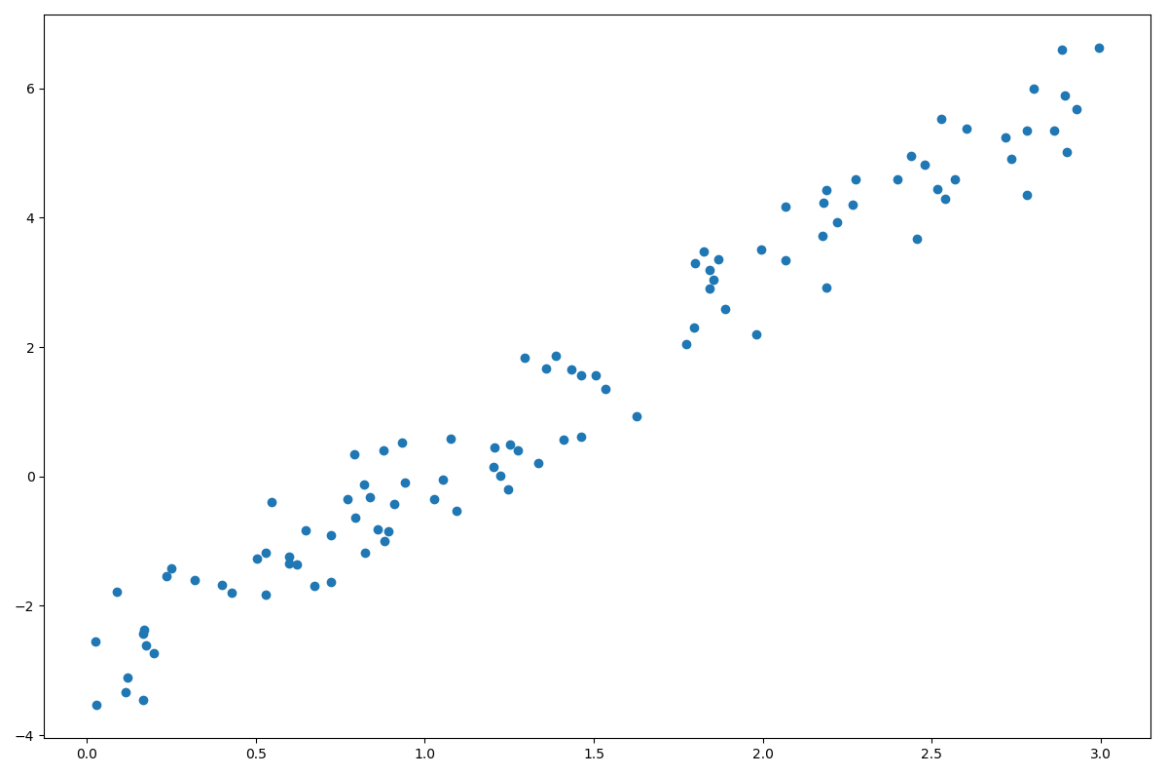
では勾配法を使って回帰します。まずはモデルを定義します。今回はこのデータにいい感じに刺さる直線が欲しいですよね。よって今回はモデルを次のように定義します。

$\hat{y} = m x + b$

はい、次は目的関数を定義します。再度状況確認しましょう。

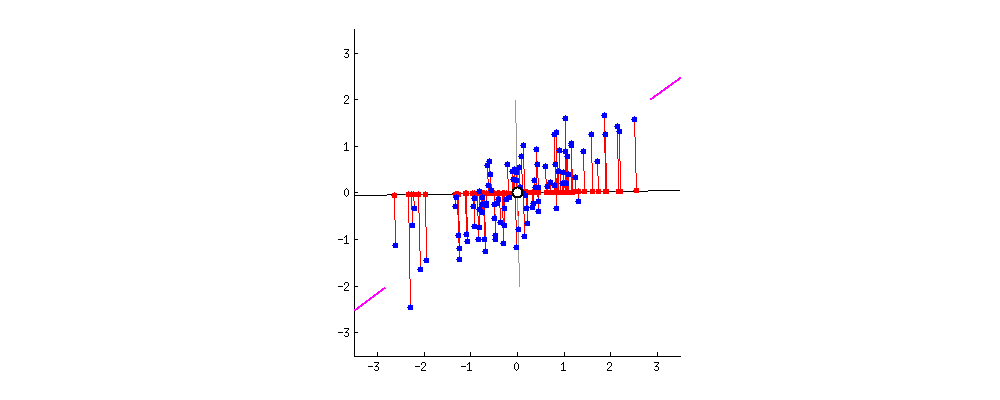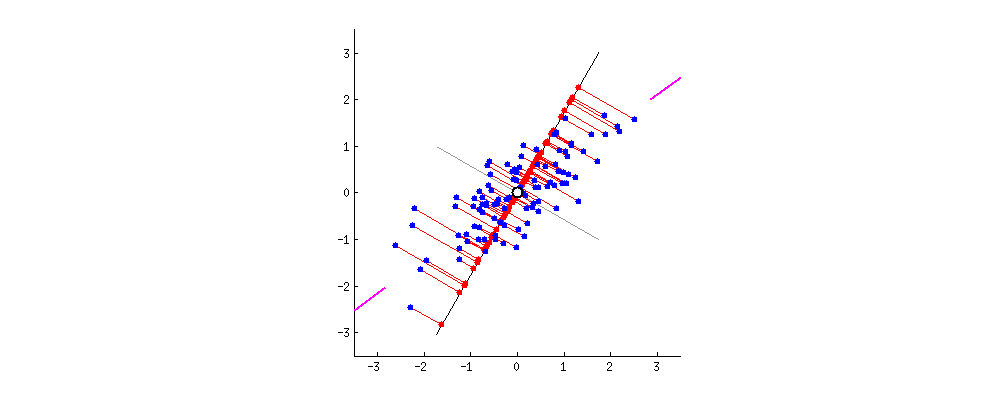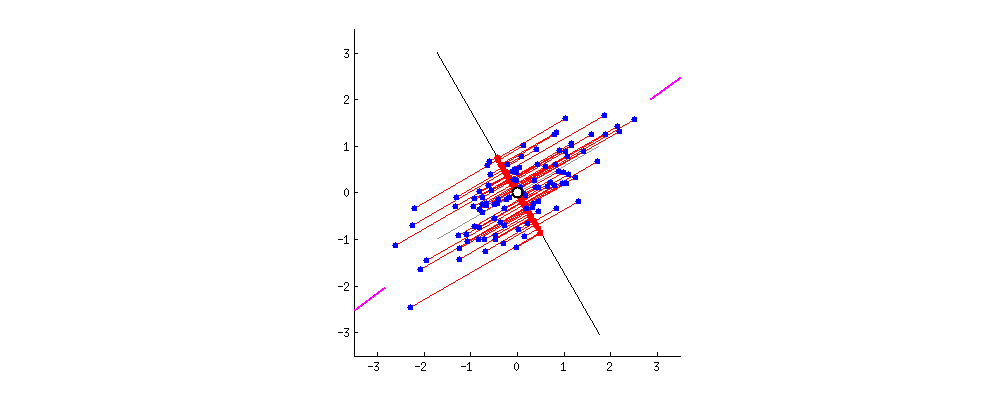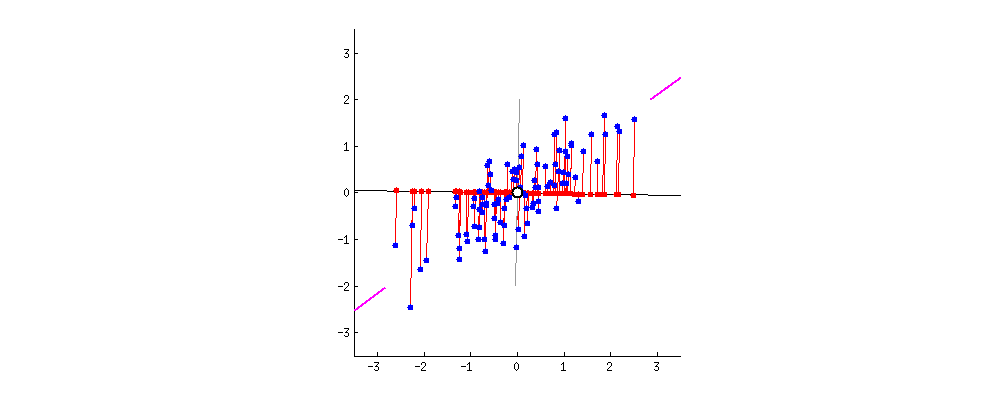
みての通りどんなにいい線を引いても「誤差(赤い線)」がありますよね。仕方ないです。現実のデータには誤差があります。これをよくNOISEと言います。とはいえ、各データの誤差の和（赤い線の和）が最小の時が一番いい線です。よって

$error = y - \hat{y} = y - ( mx + b )$

を最小化したいですよね。けどこのままだと扱いずらいので損失関数を $error = |y - ( mx + b )|$ とするとどうでしょうか。微分できないのであんまり良くないです。なのでこうしましょう。

$error = (y - ( mx + b ))^2$

微分可能であり、さらに下に凸の凸関数ですね。凸関数って何がいいんでしたっけ？そうです、お椀型なので勾配法をかけると大域最適解がゲットできます。よって今回のコスト関数はこれの和になるので

$E = \frac{1}{N} \sum_{I=1}^{N} (y_i - ( mx_i + b ))^2$

ではそれぞれ勾配を求めましょう。

$\frac{\partial E}{\partial m} = \frac{2}{N} \sum_{I=1}^{N} (-2x_i) (y_i - ( mx_i + b ))$

$\frac{\partial E}{\partial b} = \frac{2}{N} \sum_{I=1}^{N} (-2) (y_i - ( mx_i + b ))$

今回は２次元のデータだったので簡単でした、変数が増えてもやることは同じです。ちなみにこれは線形ですが曲げたければモデルを２次式・３次式、、、にすればいいですし、周期性があれば三角関数にしてもいいですし、そこは自由です。ただ現実のデータは可視化できないのが多いと思うので今回のように予想は立てられないと思います。

データが可視化できない？

いえいえ、機械学習の力を使えばできるんです。その名も

PCA

主成分分析とも言います。高次元空間のデータを低次元空間へピョンと飛ばすテクニックです。例えば500次元のデータを２次元に変換するとx-y平面で可視化できますね。便利便利。おっと話が逸れてしまいました。ところで今回の実装テーマの「線形回帰」についてですがそもそも「回帰」ってなんでしょう？

いろんな捉え方がありますが、今回の線形回帰で得られるのはいい直線でしたよね。言い換えると「xとy」をうまく結びつけてるヤツですよね？なので新しく 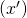$(x')$ というデータを得た時このモデルに適応させると 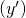$(y')$ が得られますよね。逆も同じです。
他には　
$y = 12x_1^2 + 8x_2 - 62$
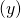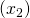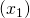というモデルだとわかった時に、目的変数 $(y)$ の値が説明変数 $(x_2)$ に比べて $(x_1)$ に強く依存することがわかります。つまり目的変数に対する寄与度が相対的にわかるんです。ちなみにこれも手法があってLasso Regression, Ridge Regression, ElasticNet Regressionなどあります。
あとはこれは僕の中では回帰っぽくないのですがロジスティック回帰です。これは分類に使われます。一見回帰はデータをうまく表現するモデルを得ることと思っちゃうんですが分類にも使えるんですね。