こんにちは。
今回のテーマは「微分」です。高校生に戻りましょう。微分の定義を覚えていますか?![]() の微分は
の微分は![]() ですよね。これを定義により確認しましょう。微分したい関数を
ですよね。これを定義により確認しましょう。微分したい関数を![]() とするとその微分は次のような定義でした。
とするとその微分は次のような定義でした。
![]()
そうです。これを使って微分を計算するのが差分法です。僕はこれを先生に教えてもらったのですが調べてみると微分方程式を解くための方法なんですね。どちらが正しいかわかりませんがとりあえず微分の定義により微分を計算することを差分法というのでしょう。
では次の微分を考えてみましょう。
![]()
では微分していきましょう。
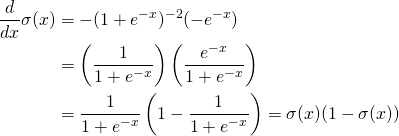
合成関数の微分でした。なんだか奇妙な形ですね。ところで元の関数![]() はどんな形かプロットして見てみましょう。
はどんな形かプロットして見てみましょう。
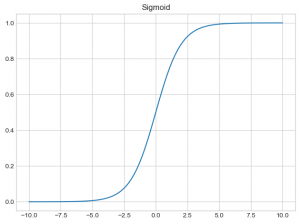
画像では![]() になっていますが、定義域は
になっていますが、定義域は![]() であり、値域は
であり、値域は![]() です。実はこの関数有名なもので「シグモイド関数」と言います。
です。実はこの関数有名なもので「シグモイド関数」と言います。
定義域と値域よりこの関数は確率を返す関数としてみることができます。実際、ニューラルネットワークやロジスティック回帰で使われています。
ところでこの導関数はどんな形でしょうか?気になりませんか?見てみましょう。
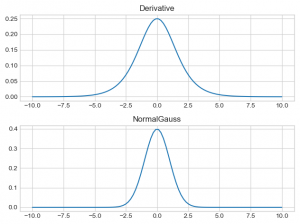
おっとこれはなんとも正規分布みたいですね。ガウス分布を知らない人のために見比べてみましょう。
非常に似てますね。そしてここで重要なのがシグモイド関数の導関数の値域です。グラフから最大値が![]() であることがわかります。この事実が後々重要になるので頭の片隅に置いておいてください。少し詳しくいうと多層パーセプトロン(ニューラルネットワーク)で「勾配消失」という問題はここに起因してます。
であることがわかります。この事実が後々重要になるので頭の片隅に置いておいてください。少し詳しくいうと多層パーセプトロン(ニューラルネットワーク)で「勾配消失」という問題はここに起因してます。
話が逸れてしまいました。全然差分法使ってねーじゃん。っていわれるかもしれません、なのでそろそろ差分法を使いましょう、と言いたいところですが記事が長くなるので実装編で会いましょう。
指摘、アドバイス、お願いします