ニュートン法を実装

こんにちは。

前回はニュートン法について学んだので今回はPythonを使って簡単な実装をしましょう。

今回はをニュートン法によって求めます。よって非線形方程式は

   

となります。必要なのは微分なのでとすると

   

となります。

区間を考えるとこれは仮定を満たすのでから始めていきましょう。実行結果は以下です。

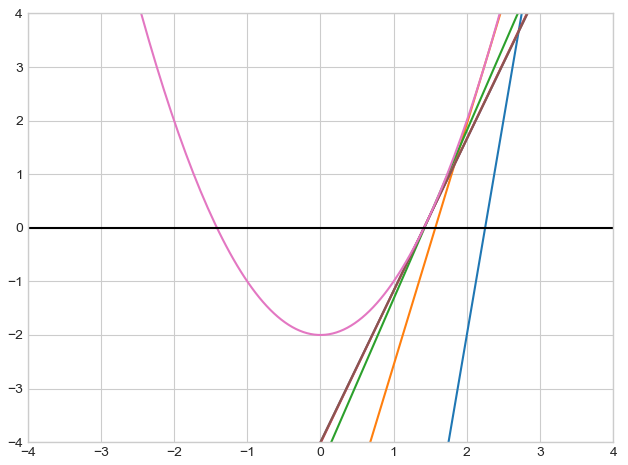
見にくいですねすいません。plotの技量を上げておきます（涙）。

ピンクの曲線がです。黒線がの直線です。そしてからニュートン法を始め、接線を順番に引いています。

最適解の更新の様子は次の通りです。

<

p style=”text-align: center;”>初期値 4
只今 2.25
只今 1.5694444444444444
只今 1.4218903638151426
只今 1.4142342859400734
収束 1.4142135625249321

「ひとよひとよにひとみごろ」でしたっけ？ちゃんと近づいてますね。ニュートン法がうまくいっているようです。

また、上の収束とはあらかじめこちらで設定していた範囲にxの更新幅が収まった時に表示させてます。（ループブレイクの条件です）

今回は簡単すぎましたが、ニュートン法は勿論、多次元にも使えます。僕の知ってる応用ではSVM(サポートベクターマシーン)の最適解を探す際にニュートン法を使った例があります。

 

ところで「微分」について少し考えてみましょう。今回、扱った関数は単純だったので幸い微分は容易でした。しかし、めちゃくちゃ複雑な関数を微分する必要が生じた時に自分の微分計算に自信をもてますか？また、微分自体どうすれば良いんや。。となった時困りますよね。実際僕はあまり計算が得意でないので微分が間違っていてもおかしくありません。。。次回はそんな問題の解決方法について紹介します。

 

指摘＆アドバイスお願いします。